辽宁省丹东市2021-2022学年九年级上学期期中考试数学试题（word版 含答案）

2021—2022学年度九年级月考 

数学试卷  

时间:120分钟    满分:150分

一．选择题（共8题，16分）

1.下列方程是关于x的一元二次方程的是（　）

A.   B.    C.    D.

2.右侧的几何体的左视图是（　）

3. 顺次连接一个四边形的各边中点，得到了一个矩形，则下列四边形中满足条件的是（　）
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.

A.①③             B.②③          C.③④               D.②④

4.小颖有两件上衣，分别是红色和白色，有两条裤子，分别是黑色和白色，她随机拿出一件上衣和一条裤子，恰好是白色上衣和白色裤子的概率是（　）

A.    B.     C.     D.

5.已知，则的值是（　）

A.      B.       C.        D.2

6.如图，正方形ABCD的边长为4，点E在对角线BD上，EF⊥AB，垂   足为F，若∠AEF=67.5º，则BF的长为（　）   

7.线段AB的两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段A′B′，则端点A′的坐标是（　）

A.（2，2）   B.（2，3）       C.（3，1）     D.（2，1）

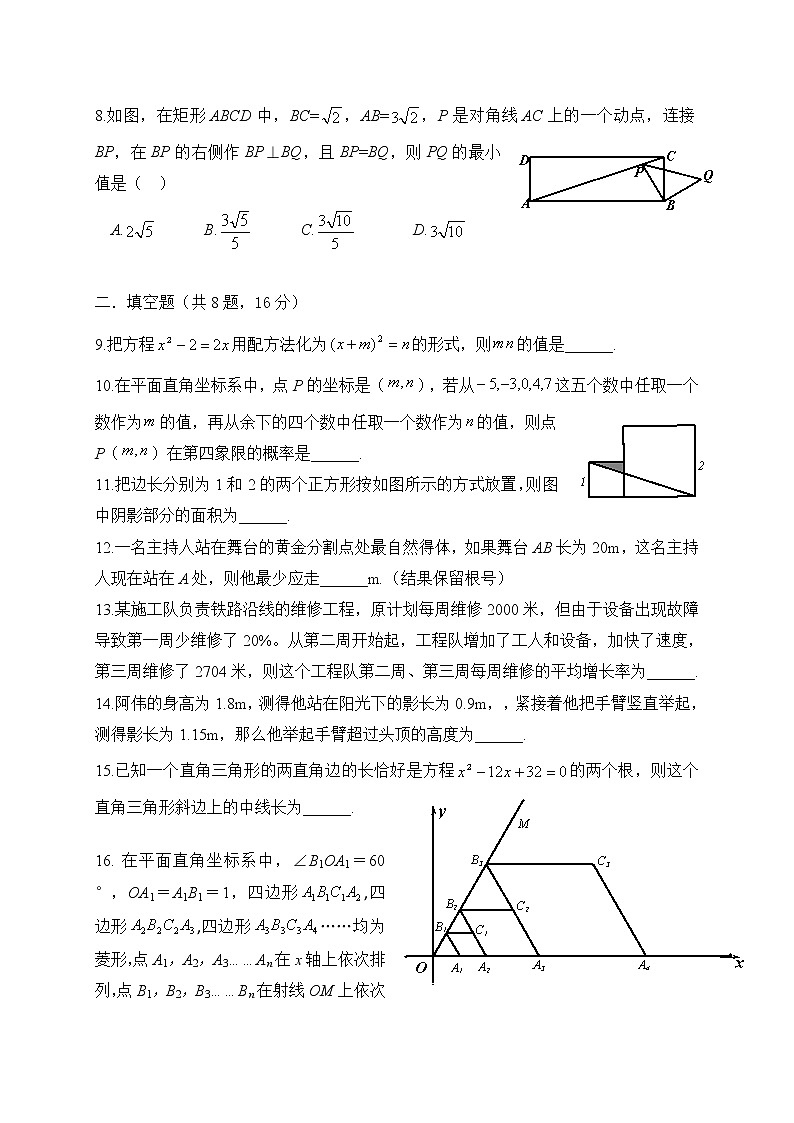
8.如图，在矩形ABCD中，BC=，AB=，P是对角线AC上的一个动点，连接BP，在BP的右侧作BP⊥BQ，且BP=BQ，则PQ的最小值是（　）

A.      B.      C.       D.

二．填空题（共8题，16分）

9.把方程用配方法化为的形式，则的值是______.

10.在平面直角坐标系中，点P的坐标是（），若从这五个数中任取一个数作为的值，再从余下的四个数中任取一个数作为的值，则点P（）在第四象限的概率是______.

11.把边长分别为1和2的两个正方形按如图所示的方式放置，则图中阴影部分的面积为______.

12.一名主持人站在舞台的黄金分割点处最自然得体，如果舞台AB长为20m，这名主持人现在站在A处，则他最少应走______m.（结果保留根号）

13.某施工队负责铁路沿线的维修工程，原计划每周维修2000米，但由于设备出现故障导致第一周少维修了20%。从第二周开始起，工程队增加了工人和设备，加快了速度，第三周维修了2704米，则这个工程队第二周、第三周每周维修的平均增长率为______.

14.阿伟的身高为1.8m，测得他站在阳光下的影长为0.9m，，紧接着他把手臂竖直举起，测得影长为1.15m，那么他举起手臂超过头顶的高度为______.

15.已知一个直角三角形的两直角边的长恰好是方程的两个根，则这个直角三角形斜边上的中线长为______.

16. 在平面直角坐标系中，∠B1OA1＝60°，OA1＝A1B1＝1，四边形,四边形,四边形……均为菱形，点A1，A2，A3……An在x轴上依次排列，点B1，B2，B3……Bn在射线OM上依次排列，那么点C2020的坐标为      .    

三．解答题（共10题，68分）

17. （6分）如图，在直角平面坐标系中，每个小正方形的边长均为1，△ABC各顶点的坐标分别为A（3，-1），B（2，-5），C（1，-2）；

（1）把△ABC向左平移4个单位，再向上平移3个单位得到△A＇B＇C＇，请画出△A＇B＇C＇并写出C＇的坐标；

（2）以点O为位似中心作△A〞B〞C〞，使得△A〞B〞C〞与△A＇B＇C＇的位似比为2∶1，且△A〞B〞C〞与△A＇B＇C＇对应顶点在同一象限内；

（3）求△A〞B〞C〞的面积；

18.（6分）（1）解方程：

（2）解方程：

19.（8分）如图，在□ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F，连接BF，AC，且AD=AF

（1）判断四边形ABFC的形状并证明；

（2）若AB=4，∠ABC=60°，求EF的长.

20.（6分）图①是一个转盘，转盘被等分成三个区域，并分别标有数字2、3、7，图②是一个正五边形的棋盘，现通过转动转盘的方式玩跳棋游戏，规则如下：将转盘转动后，看转盘指针指向的数字是几，就从图②中的A点开始在正五边形边上沿着顺时针方向连续跳过几条边（指针指向边界不计），第二次从第一次的终点处开始，按第一次的方法跳动.

（1）随机转动一次转盘，则棋子跳动到点C处的概率为      

（2）随机转动两次转盘，用画树状图或列表的方法，求棋子最终跳动到点A处的概率.

21.（8分）某商场购进一批相框，进价为每个15元.若按每个25元售出，则该商场平均每天可售出60个相框，后来经过市场调查发现，单价每降低1元，则平均每天的销量可增加10个.为尽快减少库存，该商场将相框售价进行调整，结果当天销售相框获利630元，则该相框调整后的售价是每个多少元?

22.（8分）如图，路灯OE距地面8米，身高为1.6米小明同学从距离灯的底部（点O）20米的G处，沿OG所在的直线行走14米到点M处，请通过计算说明小明前后的影长是变长还是变短？变化多少米？

23.（8分）如图，在Rt△ABC中，∠ABC=90°，AB=3cm，BC=6cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，若P，Q分别从A，B同时出发移动的时间记为t s.

（1）当t为何值时，△PBQ的面积为2.

（2）当t为何值时，以点P，B，Q为顶点的三角形与△ABC相似.

24.（8分）如图，∠ABD=∠BCD=90°，DB平分∠ADC，过点B作BM∥CD交AD于点M，连接CM.

（1）求证：△ABD∽△BCD；

（2）若CD=4，AD=6，求MC的长.

25.（10分）已知四边形ABCD和EFCG,连接AC，EC，直线AE与直线BF交于点H.

（1）观察与猜想

如图1，当四边形ABCD和EFCG均为正方形时，线段AE和BF的数量关系是　   　；∠AHB＝　   　．

（2）探究与证明

如图2，当四边形ABCD和FFCG均为矩形，且∠ACB＝∠ECF＝30°时，试探究线段AE和BF的数量关系以及∠AHB的度数，并证明你的结论.

（3）在（2）的条件下，若BC＝，FC＝，将矩形EFCG绕点C旋转，在整个旋转过程中，当A、E、F三点共线时，请直接写出点B到直线AE的距离．

2021-2022九年级月考数学试题参考答案

一.选择题（每题3分，共24分）

二.填空题（每题3分，共24分）

三.解答题（共102分）

17.

(1)如图；………………（4分）

(2)C’(-3,1)；………………（6分）

(3)S=14………………（8分）

18.（1）………………（4分）

（2）原式=，代数求值为………………（10分）

19.(1)矩形，理由如下：

∵□ABCD

∴AB∥CD,即AB∥DF，AD=BC

∴∠ABC=∠BCF

又∵BE=CE

∴△ABE≌△FCE

∴AB=CF

∵AB∥CF

∴四边形ABFC为平行四边形………………（4分）

∵AD=BC,AD=AF

∴BC=AF

∴四边形ABFC为矩形………………（6分）

（2）∵四边形ABFC为矩形

∴AE=EF，BE=CE，BC=AF

又∵∠ABC=60°

∴三角形ABE为等边三角形………………（8分）

∴AE=AB=4

∴EF=4………………（10分）

20.(1) ………………（2分）

(2)

………………（6分）

由列表可知，共有9种等可能结果，其中两次和为5或者10的有4次………………（8分）

∴P（转到A处）=  ………………（10分）

树状图评分同上

21.解：设每个相框降价为x元，根据题意，得………………（1分）

）=630………………（5分）

解得，………………（7分）

∵为尽快减少库存∴………………（8分）

25-3=22元………………（9分）

答：每个相框售价为22元。………………（10分）

其它方法评分同上

22.解：OM=OG-GM=20-14=6

由题意可得△BHG∽△BEO，△ANM∽△AEO

∴………………（6分）

即

∴BG=5,AM=1.5………………（8分）

∵5-1.5=3.5………………（9分）

∴小明前后的影长是变短了，短了3.5米………………（10分）

23.解：

（1）由题意得：

………………（2分）

∴………………（4分）

(2) 由题意得：△BPQ∽△BAC或△BPQ∽△BCA

则有………………（8分）

故

∴………………（10分）

24.解：（1）

∴………………（4分）

（2）

∴………………（7分）

∵

∴………………（8分）

∴………………（10分）

25.（1）∵DB平分∠ADC

∴∠ADB=∠CDB

双∵∠ABD=∠BCD=90°

∴△ABD∽△BCD………………（4分）

（2）由（1）得

∴BD2=24

在Rt△BCD中，由勾股定理得BC2=8

∵BM∥CD

∴∠MBD=∠BDC

∵∠ADB=∠BDC

∴∠ADB=∠MBD

∴BM=DM………………（6分）

∵∠A+∠ADB=90°, ∠ABM+MBD=90°

∴∠A=∠ABM

∴AM=BM………………（8分）

∴BM=

在Rt△BCM中，由勾股定理得CM2=BM2+BC2=9+8=17

∴………………（10分）

26.(1), ∠ABH=45°………………（4分）

(2)由△ACE∽△BCF

∴，∠CAE=∠CBF………………（8分）

由三角形内角和可得，∠ABH=∠ACB=30°………………（9分）

∴………………（10分）

(3) ………………（14分）