人教版六年级上册数学5.7扇形的认识+考点+课本习题+PPT课件【易懂通课堂】

这是一份null，共30页。PPT课件主要包含了什么是扇形，圆心角，特殊的扇形，填空题等内容，欢迎下载使用。

这些物体的外形有什么相同的地方吗？
它们的外形都是扇形的。
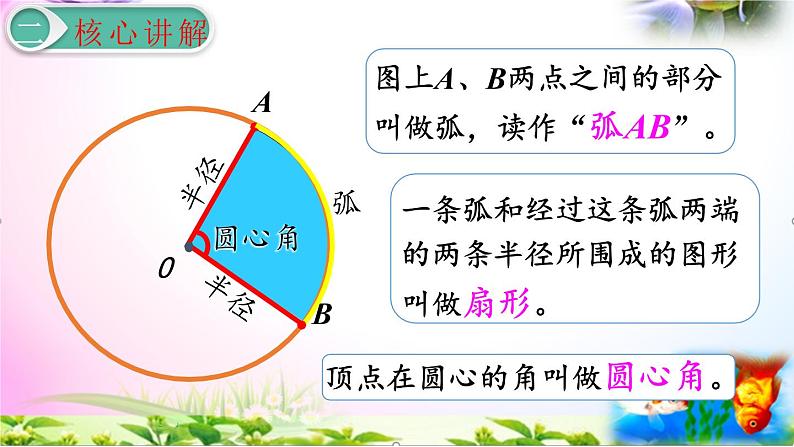
图上A、B两点之间的部分叫做弧，读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
即时练习：指出下列物体中的扇形。
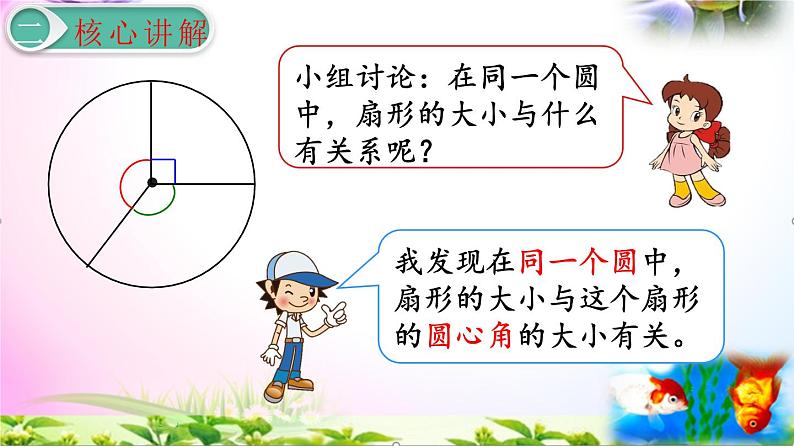
小组讨论：在同一个圆中，扇形的大小与什么有关系呢？
我发现在同一个圆中，扇形的大小与这个扇形的圆心角的大小有关。
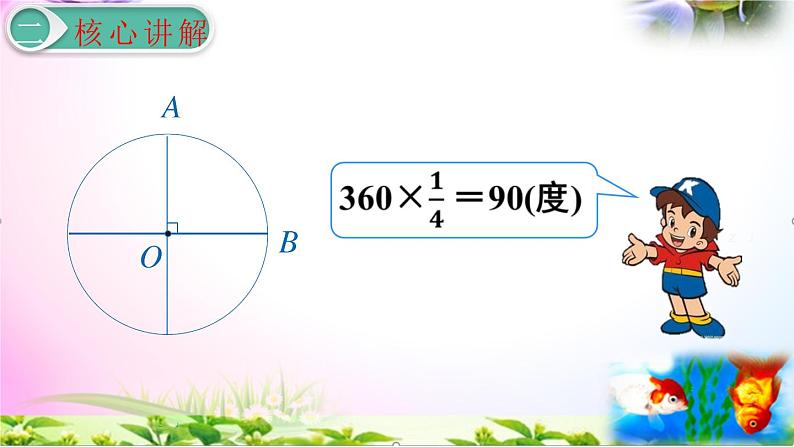
以半圆为弧的扇形的圆心角是180°。
1.一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。扇形是圆的一部分。 2.在同一个圆中，圆心角越大，扇形越大；在不同的圆中，圆心角相同的扇形，半径越大，扇形越大。
1. 指出下列物体中的扇形。
（1）扇形都有一个角，这个角的顶点在（ ）。（2）同一个圆中，扇形的大小与这个扇形的 （ ）的大小有关。（3）一个圆可以分成（ ）个圆心角是180° 的扇形。
3．求下面扇形的周长与面积。
4.下列每个正方形边长是2㎝，求阴影部分的 面积。
×3.14×22 -2×（2×2）÷2 =6.28-4=2.28（cm2)答：阴影部分的面积为2.28 cm2。
下面图形的阴影部分是扇形的画“√”。
5．“圆心角越大，扇形的面积就越大”这句话对吗？为什么？
不对，扇形的大小由半径长短和圆心角大小两个条件决定。
辨析：扇形面积的大小与半径也有关系，所以在判断扇形面积大小时不仅要考虑圆心角，还需要考虑半径。
5.如图，图形的半径是5cm，涂色部分所表示的扇形的圆心角是60°，求扇形的面积。(得数保留整数）
5×5×3.14＝78.5（平方厘米）60°÷360°＝78.5× ≈13（平方厘米）答：扇形的面积是13平方厘米。
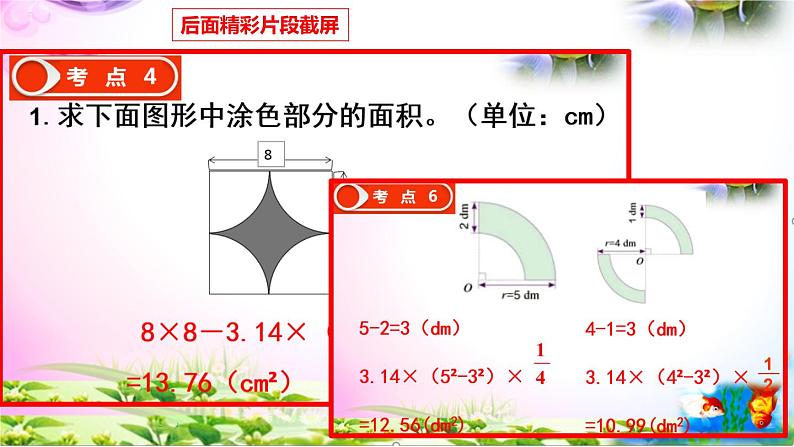
1.求下面图形中涂色部分的面积。（单位：cm）
8×8－3.14×（8÷2）²=13.76（cm²）
5.你在生活中见过下面这些图案吗？
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗？
4-1=3（dm）3.14×（4²-3²）× =10.99(dm2)
1.在同一个圆中，圆心角越大，扇形越大；在不同的圆中，圆心角相同的扇形，半径越大，扇形越大。2.扇形的面积占圆的面积的几分之几与扇形的圆心角度数占360°的几分之几相同。
6．求阴影部分的面积。