






- 专题突破1 运动图像 追及与相遇问题学案 学案 6 次下载
- 第1讲 重力、弹力、摩擦力课件PPT 课件 5 次下载
- 第3讲 受力分析 共点力的平衡及应用课件PPT 课件 4 次下载
- 实验_探究弹簧弹力与形变量的关系课件PPT 课件 3 次下载
- 实验_探究两个互成角度的力的合成规律课件PPT 课件 3 次下载
第2讲 力的合成与分解课件PPT
展开1.合力与分力(1)定义:如果一个力 产生的效果 跟几个力共同作用产生的效果相同,这 一个力就叫那几个力的 合力 ,那几个力就叫这个力的 分力 。(2)关系:合力和分力是一种 等效替代 关系。注意 合力不一定大于分力,二者是等效替代的关系,受力分析时不可同时作 为物体所受的力。
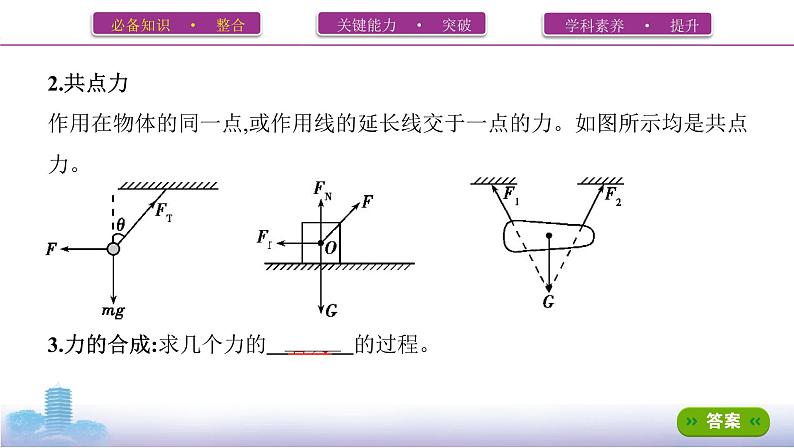
2.共点力作用在物体的同一点,或作用线的延长线交于一点的力。如图所示均是共点 力。
3.力的合成:求几个力的 合力 的过程。
4.力的运算法则 (1)三角形定则:把两个矢量 首尾相连 从而求出合矢量的方法。(如图所示)(2)平行四边形定则:求互成角度的 两个力 的合力,可以用表示这两个力 的线段为邻边作 平行四边形 ,这两个邻边之间的对角线就表示合力的 大小 和 方向 。
1.力的分解(1)定义:求一个力的 分力 的过程。力的分解是 力的合成 的逆运算。(2)遵循的原则: 平行四边形 定则或三角形定则。
2.力的效果分解法(1)根据力的 实际作用效果 确定两个实际分力的方向;(2)再根据两个实际分力的方向画出 平行四边形 ;(3)最后由数学知识求出两分力的大小。
3.正交分解法(1)定义:将已知力按 互相垂直 的两个方向进行分解的方法。(2)建立坐标轴的原则:以少分解力和容易分解力为原则(即尽量多的力在坐 标轴上)。
三、矢量和标量1.矢量:既有大小又有 方向 的物理量,相加时遵从 平行四边形定则 。2.标量:只有大小 没有 方向的物理量,求和时按 代数法则 相加。注意 矢量与标量的根本区别在于运算法则,矢量运算使用平行四边形定则 或三角形定则,而标量运算使用代数运算法则。
1.判断下列说法对错。(1)合力与它的分力的作用对象为同一个物体。 ( )(2)合力及其分力可以同时作用在物体上。 ( )(3)几个力的共同作用效果可以用一个力来代替。 ( )(4)在进行力的合成与分解时,都要应用平行四边形定则或三角形定则。 ( )(5)两个力的合力一定比其分力大。 ( )(6)既有大小又有方向的物理量一定是矢量。 ( )
2.(新人教版必修第一册P71·T4改编)一个竖直向下的180 N的力分解为两个 分力,一个分力在水平方向上且大小为240 N,则另一个分力的大小为 ( )A.60 N B.240 N C.300 N D.420 N
3.减速带是交叉路口常见的一种交通设施,车辆驶过减速带时要减速,以保障 行人的安全。当汽车前轮刚爬上减速带时,减速带对车轮的弹力为F,图中弹 力F的画法正确且分解合理的是 ( )
1.[矢量三角形的应用](2020湖北黄石模拟)如图所示,AB是半圆的直径,O为圆 心,P点是圆上的一点,在P点有三个共点力F1、F2、F3。若F2的大小已知,则这 三个力的合力大小为 ( ) A.F2 B.2F2 C.3F2 D.4F2
2.[平行四边形的应用]射箭是奥运会上一个观赏性很强的运动项目,中国队 有较强的实力。如图甲所示,射箭时,刚释放的瞬间,若弓弦的拉力为100 N,对 箭产生的作用力为120 N,弓弦的拉力如图乙中F1和F2所示,对箭产生的作用 力如图乙中F所示,则弓弦的夹角α应为(cs 53°=0.6) ( ) A.53° B.127° C.143° D.106°
解析 弓弦拉力的合成如图所示,由于F1=F2,由几何知识得2F1 cs =F合,有cs = = = =0.6所以 =53°
即α=106°,故D正确。
1.合力大小的范围(1)两个共点力的合成:|F1-F2|≤F≤F1+F2。即两个力的大小不变时,其合力随夹角的增大而减小,当两个力共线反向时, 合力最小,为|F1-F2|;当两力共线同向时,合力最大,为F1+F2。(2)三个共点力的合成。①三个力共线且同向时,其合力最大为F=F1+F2+F3;②以这三个力的大小为边,如果能组成封闭的三角形,则其合力最小值为零, 若不能组成封闭的三角形,则合力最小值等于最大的一个力减去另外两个力 的大小之和。
2.共点力合成的常用方法(1)作图法:从力的作用点起,按同一标度作出两个分力F1和F2的图示,再以F1和 F2的图示为邻边作平行四边形,画出过作用点的对角线,量出对角线的长度, 计算出合力的大小,量出对角线与某一力的夹角确定合力的方向(如图所 示)。 (2)计算法:几种特殊情况的共点力的合成。
(3)力的三角形定则:将表示两个力的线段保持原来的方向依次首尾相 接,从第一个力的起点,到第二个力的箭头的有向线段为合力。平行四边形定 则与三角形定则的关系如图所示。
3.重要结论(1)两个分力大小一定时,夹角θ越大,合力越小。(2)合力一定,两等大分力的夹角越大,两分力越大。(3)合力可以大于分力,等于分力,也可以小于分力。
1.按力的效果分解(1)根据力的实际作用效果 两个实际分力的方向;(2)再根据两个实际分力方向 平行四边形;(3)最后由三角形知识 两分力的大小。
2.正交分解法(1)定义:将已知力按互相垂直的两个方向进行分解的方法。(2)建立坐标轴的原则:一般选共点力的作用点为原点。在静力学中,以少分 解力和容易分解力为原则(即尽可能让更多的力在坐标轴上);在动力学中,以 加速度方向和垂直加速度方向为坐标轴建立坐标系。
(3)应用:物体受到多个力作用F1、F2、F3…,求合力F时,可把各力沿相互垂直的x轴、y轴分解(如图)。x轴上的合力:Fx= + + +…y轴上的合力:Fy= + + +…合力的大小:F= 合力方向:与x轴夹角为θ,则tan θ= 。
3.力的分解的唯一性和多解性(1)已知两个不平行分力的方向,可以唯一地作出力的平行四边形,对力进行 分解,其解是唯一的。(2)已知一个分力的大小和方向,力的分解也是唯一的。(3)已知一个分力F1的方向和另一个分力F2的大小,对力F进行分解,如图所示, 有三种可能:(F1与F的夹角为θ)
①F2
审题关键 (1)金属球的重力产生哪两个作用效果?提示:压紧BC面和压紧AB面。(2)金属球对凹槽AB边和BC边的压力F1和F2是金属球重力的分力吗?提示:不是。
解析 金属球受到的重力产生两个作用效果,压紧AB面和压紧BC面,如图 所示,将金属球所受的重力分解为压紧AB面的力F1'和压紧BC面的力F2',又由 题意知,F1=F1',F2=F2',故 =tan 30°= ,故C项正确。
解题感悟力的合成与分解方法的选择力的效果分解法、正交分解法、合成法都是常见的解题方法,一般情况下,物 体只受三个力的情形下,力的效果分解法、合成法解题较为简单,在三角形中 找几何关系,利用几何关系或三角形相似求解;而物体受三个以上力的情况多 用正交分解法,但也要视题目具体情况而定。
1.[力的分解的应用](2020山东威海二模)生活中经常用刀来劈开物体。如图 是刀刃的横截面,F是作用在刀背上的力,若刀刃的横截面是等腰三角形,刀刃 两侧面的夹角为θ,刀的重力可以忽略,则刀劈物体时对物体的侧向推力FN的 大小为 ( )A. B.
C.F cs D.
解析 将力F根据平行四边形定则分解如下:由几何知识得,侧向推力的大 小为FN= = ,故A、C、D错误,B正确。
2.[正交分解法的应用](2020河北衡水调研)如图所示,质量为m的物体置于倾 角为θ的固定斜面上,物体与斜面之间的动摩擦因数为μ。先用平行于斜面的 推力F1作用于物体上使其能沿斜面匀速上滑,之后改用水平推力F2作用于物 体上,也能使物体沿斜面匀速上滑,则两次的推力大小之比 为 ( )
A.cs θ+μ sin θ B.cs θ-μ sin θC.1+μ tan θ D.1-μ tan θ
解析 物体在力F1作用下和力F2作用下运动时的受力如图所示。将物体受 力沿斜面方向和垂直于斜面方向正交分解,由平衡条件可得:F1=mg sin θ+Ff1, FN1=mg cs θ,Ff1=μFN1,F2 cs θ=mg sin θ+Ff2,FN2=mg cs θ+F2 sin θ,Ff2=μFN2,解 得F1=mg sin θ+μmg cs θ,F2= ;故 =cs θ-μ sin θ,选项B正确。
考点三 “活结”与“死结”、“动杆”与“定杆”问题
考向一 “活结”与“死结”问题
例2 (多选)(2017天津理综,8,6分)如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架挂钩是光滑的,挂于绳上处于静止状态。如果只人为改变一个条件,当衣架静止时,下列说法正确的是 ( )
A.绳的右端上移到b',绳子拉力不变B.将杆N向右移一些,绳子拉力变大C.绳的两端高度差越小,绳子拉力越小D.若换挂质量更大的衣服,则衣架悬挂点右移
审题关键 (1)绳的右端上移过程中,两段绳子间的夹角怎样变化?提示:不变。(2)将杆N向右移一些,两段绳子间夹角将怎样变化?提示:变大。
解析 本题考查物体受力分析、物体的平衡。衣架挂钩为“活结”模 型,a、b为一根绳,两端拉力相等,设绳ab长为L,M、N的水平距离为d,b延 长线交M于a',由几何知识知 a'=a,sin θ= ,由平衡条件有2F cs θ=mg,则F= ,当b上移到b'时,d、L不变,θ不变,故F不变,选项A正确,C错误。将杆N向右移一些,L不变,d变大,θ变大,cs θ 变小,则F变大,选项B正确。只改变m,其他 条件不变,则sin θ不变,θ不变,衣架悬挂点不变,选项D错误。
解题感悟“死结”与“活结”问题(1)“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。“死 结”两侧的绳因“结”而变成了两根独立的绳,因此由“死结”分开的两段 绳子上的弹力不一定相等。(2)“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。“活结” 一般由绳跨过滑轮或者绳上挂一光滑挂钩而形成。绳子虽然因“活结”而 弯曲,但实际上“活结”两侧的绳子是同一根绳,所以由“活结”分开的两段 绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
考向二 “动杆”与“定杆”问题
例3 如图甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮挂住一个质 量为M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一 端G通过细绳EG拉住,EG与水平方向也成30°角,轻杆的G点用细绳GF拉住一 个质量为M2的物体,(重力加速度为g)求:
(1)细绳AC段的张力FTAC与细绳EG的张力FTEG之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力。
审题关键 (1)图中杆上的力一定沿杆吗?提示:题图甲杆上的力不沿杆,题图乙杆上的力沿杆。(2)两图中分别以谁为研究对象?提示:C点、G点。
答案 (1) (2)M1g 方向与水平方向成30°指向右上方 (3) M2g,方向水平向右
解析 题图甲和乙中的两个物体都处于平衡状态,根据平衡条件,首先判断与 物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象, 进行受力分析,如图甲和乙所示,根据平衡条件可求解。 (1)图甲中细绳AD跨过定滑轮拉住质量为M1的物体,物体处于平衡状态,细绳 AC段的拉力
FTAC=FTCD=M1g图乙中由FTEG sin 30°=M2g,得FTEG=2M2g。所以 = 。(2)图甲中,三个力之间的夹角都为120°,根据平衡条件有FNC=FTAC=M1g,方向与 水平方向成30°指向右上方。(3)图乙中,根据平衡方程有FTEG sin 30°=M2g,FTEG cs 30°=FNG,所以FNG=M2g ct 30°= M2g,方向水平向右。
解题感悟“动杆”与“定杆”问题(1)动杆:对一端有光滑转轴O的静止轻杆而言,轻杆受力平衡时,轻杆的另一 端受到的力一定沿轻杆的方向,如图甲所示,轻杆OB静止时,轻绳ABC对轻杆 OB的作用力一定沿BO方向,否则轻杆将会绕光滑轴O转动,与已知杆静止条 件矛盾。
(2)定杆:图乙中,轻杆是插入墙中的,这时A'B'C'对轻杆O'B'的作用力就不一定 沿B'O'方向。
科学思维——对称法解决非共面力问题
1.学科素养解读——科学思维能力的培养在力的合成与分解的实际问题中,经常遇到物体受多个非共面力作用处于平 衡状态的情况,而在这类平衡问题中,又常有图形结构对称的特点,结构的对 称性往往对应着物体受力的对称性。
2.解题策略技巧——对称法的应用解决这类问题的方法是根据物体受力的对称性,结合力的合成与分解知识及 平衡条件列出方程,求出结果。
例4 叠放在水平地面上的四个完全相同的排球如图所示,质量均为m,相互接触,球与地面间的动摩擦因数都是μ。底层三个排球刚好接触成三角形,上层一个排球放在底层三个排球的正中间上方,系统保持静止。不考虑球的转动和球与球间的摩擦力,若最大静摩擦力等于滑动摩擦力,重力加速度为g,则 ( )
A.底层每个排球对地面的压力均为2mgB.底层每个排球对上层排球的支持力大小为 C.底层排球受到水平地面的摩擦力均为 D.水平地面与球间的动摩擦因数至少为
解析 根据整体法,下面每个球对地面的压力为N,3N=4mg,N= mg,故A错误;上层排球受到重力、下层排球对上层排球的三个支持力F,由于三个支持 力的方向不是竖直向上,所以三个支持力在竖直方向的分量之和等于重力,根 据正四面体几何关系可求,F与mg的夹角的余弦值cs θ= ,正弦值sin θ= ,则有:F cs θ+mg=NF sin θ=f联立解得f= mg,F= mg,则有μ= = ,所以水平面与球间的动摩擦因数
至少为 ,故B、C错误,D正确。
1.现场卸货历来是中国南极考察队的“硬仗”,需要利用卡特彼勒车将重达25吨的货物卸载,如图所示,吊钩下有四根一样的绳索,且四根绳索呈对称分布, 每根绳索与竖直方向的夹角均为30°,则每根绳索的拉力大小约为 ( )A.9.0×104 N B.7.0×104 NC.5.0×104 N D.3.0×104 N
2.(多选)(2020安徽滁州月考)微元法就是把研究对象分为无限多个无限小的 部分,取出有代表性的极小的一部分进行分析处理,再从局部到整体综合起来 加以考虑的科学思维方法。如图所示,静止的圆锥体竖直放置,轴截面顶角为 α、质量为m且分布均匀的链条环水平地套在圆锥体上,忽略链条与圆锥体之 间的摩擦力,在链条环中任取一小段Δl,其质量为Δm,对此部分受力分析,下列 说法正确的是 ( )
A.设圆锥体对链条环的支持力为N,则Δmg=N sin B.链条环中的张力为T,则T= C.链条环中的张力为T,则T= tan α
D.设Δl相对链条环中心的张角为Δφ,则有2T sin =N sin
解析 如图乙、丙所示,设Δl对链条环中心的张角为Δφ,根据共点力平衡 条件知,
Δl在水平方向上受力平衡,有:2T sin =N cs ①因Δl很短,Δφ很小,所以sin ≈ ②将②代入①式有:TΔφ=N cs ③Δl在竖直方向上也受力平衡,Δmg=N sin ④④代入③式得,tan = g ⑤
高考物理一轮复习课件+讲义 第2章 第3讲 力的合成与分解: 这是一份高考物理一轮复习课件+讲义 第2章 第3讲 力的合成与分解,文件包含高考物理一轮复习第2章第3讲力的合成与分解pptx、高考物理一轮复习第2章第3讲力的合成与分解docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
新高考物理一轮复习课件 第2章 第3讲 力的合成与分解: 这是一份新高考物理一轮复习课件 第2章 第3讲 力的合成与分解,共58页。PPT课件主要包含了共点力的合成,课时精练等内容,欢迎下载使用。
高中物理高考 2022年高考物理一轮复习 第2章 第3讲 力的合成与分解课件PPT: 这是一份高中物理高考 2022年高考物理一轮复习 第2章 第3讲 力的合成与分解课件PPT,共60页。PPT课件主要包含了内容索引,考点一共点力的合成,课时精练等内容,欢迎下载使用。












