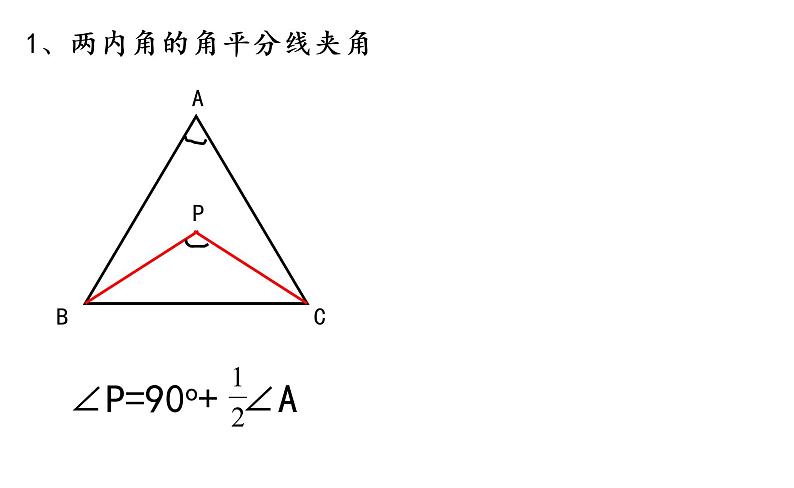
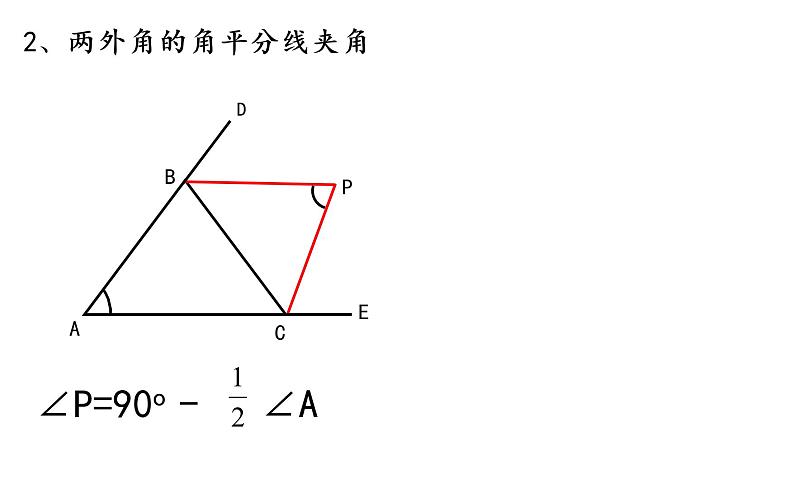
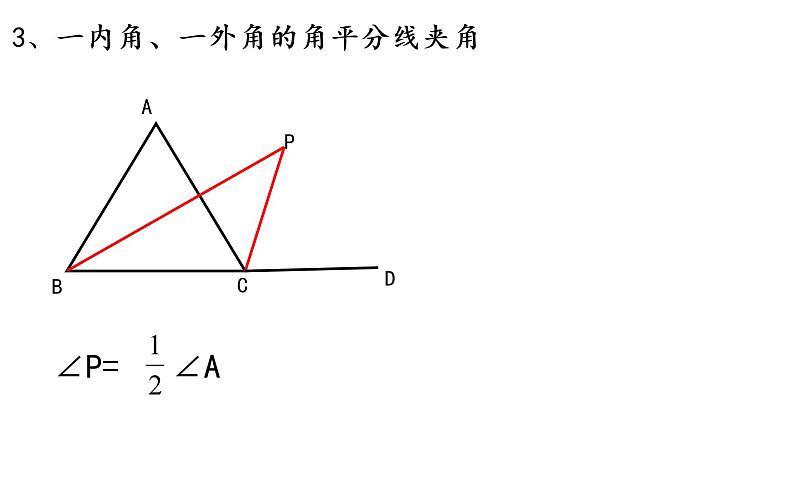
初中数学华师大版七年级下册1 用相同的正多边形优秀课件ppt

9.2多边形内角和与外角和

一、选择题：

1、一个多边形少算一个内角，其余内角之和是1500°，则这个多边形的边数是（          ）

2、已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比是3：1，这个多边形的边数是（          ）

3、若一个多边形的内角和与它的外角和相等，则这个多边形是（          ）

4、如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2的度数为（          ）
 

5、已知一个多边形的内角和是外角和的4倍，则这个多边形是（          ）

6、一个10边形的内角和等于（          ）

7、一副三角板如图所示摆放，则∠α与∠β的数量关系为（          ）
 

8、如图，在五边形ABCDE中，若去掉一个30°的角后得到一个六边形BCDEMN，则∠1+∠2的度数为（          ）
 

9、如图，小明从点A出发沿直线前进10米到达点B，向左转45°后又沿直线前进10米到达点C，再向左转45°后沿直线前进10米到达点D…照这样走下去，小明第一次回到出发点A时所走的路程为（          ）
 

10、正十边形的每一个外角的度数为（          ）

二、填空题：

1、已知多边形每个内角都等于150°，则这个多边形的内角和为                ．

2、如图，∠A=∠ABC=∠C=∠D=∠E，点F在AB的延长线上，则∠CBF的度数是               ．
 

3、如图，小明从点A出发，前进5 m后向右转20°，再前进5 m后又向右转20°，这样一直下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形，那么小明一共走了              m，这个多边形的内角和是            °． 
 

4、图1是一盏可折叠台灯．图2为其平面示意图，底座AO⊥OE于点O，支架AB，BC为固定支撑杆，∠A是∠B的两倍，灯体CD可绕点C旋转调节．现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示)，此时，灯体CD′所在的直线恰好垂直支架AB，且∠BCD-∠DCD′=126°，则∠DCD′=                 ．
 

5、如图所示的六边形花环是用六个全等的直角三角形拼成的，则∠ABC=              度．
 

三、解答题：

1、已知一个多边形的所有内角的和与它的外角之和为1620°，求这个多边形的边数n．

2、已知边数为n的多边形的一个外角是m°，内角和是x°，外角和是y°．

(1)当x=2y时，求n的值．

(2)若x+y+m=2380，求m的值．

3、如果一个多边形的内角和是外角和的3倍还多180°，那么这个多边形的边数是多少？

4、在各个内角都相等的多边形中，一个外角等于一个内角的，求这个多边形每一个内角的度数和它的边数．

5、一个多边形的内角和是它外角和的2倍，求这个多边形的边数．

答案

一、选择题：

1、【答案】D    2、【答案】A    3、【答案】B    4、【答案】C    5、【答案】C

6、【答案】C    7、【答案】B    8、【答案】A    9、【答案】B    10、【答案】A

二、填空题：

1、【答案】1800°    2、【答案】72°    3、【答案】90        2 880    4、【答案】36°   5、【答案】30

三、解答题：

1、【答案】解：设这个多边形的边数是n，
由题意得，(n-2)·180°+360°=1620°，
解得，n=9．
答：这个多边形的边数n是9．

2、【答案】(1)解：∵多边形的外角和为360°，

∴y=360，

∵n边形的内角和为(n-2)×180°，

∴x=(n-2)×180=180n-360，

∵x=2y，

∴180n-360=2×360，

解得：n=6．
(2)解：∵x+y+m=2380，

∴180n-360+360+m=2380，

即：180n+m=2380，

∵n边形的一个外角是m°，

∴m<180，

∵n为正整数，

∴n为2380÷180的整数部分，m为2380÷180的余数，

∵2380÷180=13⋯⋯40，

∴m=40．

3、【答案】解：设这个多边形的边数为n，根据题意，得：(n-2)·180=360×3+180，

解得：n=9，

则这个多边形的边数是9．

4、【答案】解：设这个多边形的每一个内角为x°，
由题意，得：180-x=x，
解得：x=140，
∴边数为360÷(180-140)=9，
则这个多边形的每一个内角的度数为140°，它的边数为9．

5、【答案】解：设这个多边形的边数是n，
根据题意得，(n-2)·180°=2×360°，
解得n=6．
答：这个多边形的边数是6．