初中数学北师大版七年级上册4.2 比较线段的长短课文配套ppt课件

这是一份初中数学北师大版七年级上册4.2 比较线段的长短课文配套ppt课件，共22页。PPT课件主要包含了想一想，练一练，两点之间线段最短，三步骤，度量已知线段，移到射线上，试一试，AB﹥CD，AB＝CD，AB﹤CD等内容，欢迎下载使用。
教学目标1、借助具体情境了解“两点之间所有连线中，线段最短”的性质。2、能借助直尺、圆规等工具比较两条线段的长短。3、能用圆规作一条线段等于已知线段。
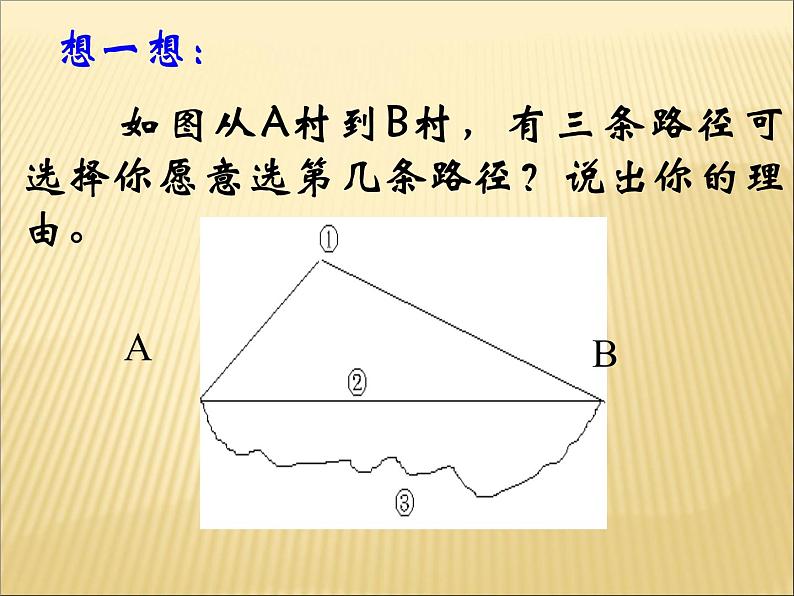
如图从A村到B村，有三条路径可选择你愿意选第几条路径？说出你的理由。
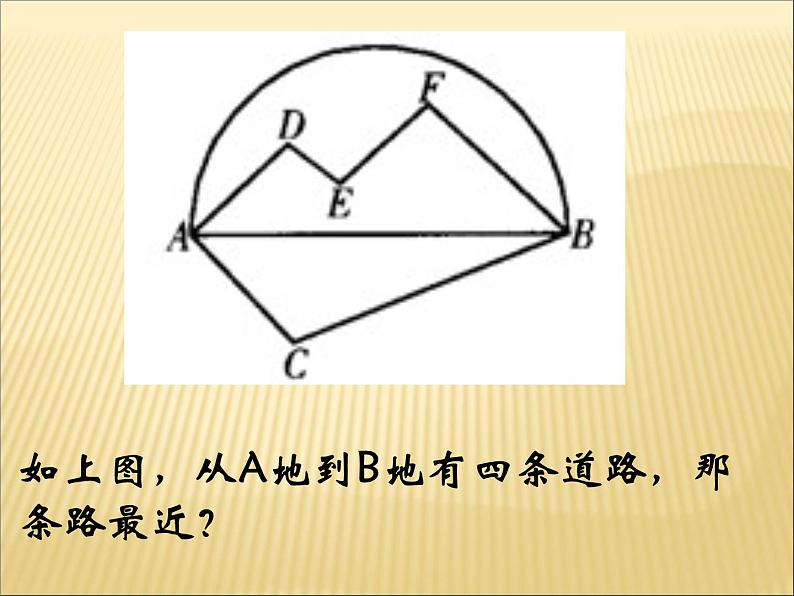
如上图，从A地到B地有四条道路，那条路最近？
线段的性质：两点之间的所有连线中，线段最短.也可简述为：“两点之间，线段最短。”两点间的距离：两点之间线段的长度。
根据生活经验，容易发现： 两点之间的所有连线中，线段最短。
（2）如图：这是A、B两地之间的公路，在公路工程改造计划时，为使A、B两地行程最短，应如何设计线路？在图中画出。你的理由是_______________________________
（1）填空：两点之间的距离是指两点之间的线段 的 ( )
例： 用直尺、圆规画一条线段等于已知线段。
第一步：先用直尺画一条射线AB．
第二步：用圆规量出已知线段的长度a．
第三步：在射线AB上点A以为圆心，截取AC=a．
1、请你用圆规和直尺画线段DE等于已知线段AB。
2、已知线段a、b，你能作一条线段c，使c= 2a+b 吗？
3、已知线段a、b，你能作一条线段c，使c= 2a-b 吗？
如何比较两条线段的大小
叠合法：把它们放在同一条直线上比较，此种方法可称之为“叠合法”。度量法：用刻度尺去度量它们的长度进行比较，此种方法可称之为“度量法”。
问题: 你如何确定一条线段的中点 ？
2、通过对折寻找线段中点
例.己知，如图，点C是线段AB上一点，点M是线段AC的中点，点N是线段BC的中点，如果AB=10cm，AM=3cm，求CN的长。
解：∵M为AC的中点，∴AC＝2AM． 又∵AM＝3cm，∴AC＝2×3＝6(cm) ． ∵AB＝10cm． ∴BC＝AB－AC＝10－6＝4(cm) ． 又∵N为BC的中点，
(2) 在直线上顺次取出A、B、C三点使AB＝4cm，BC＝3cm，如果O是线段AC的中点，求线段OB的长度？
(3) 已知线段AB＝6cm，在直线AB上画线段BC，使之等于2cm，求线段AC的长？
1、如图 AB=6cm，点C是AB的中点，点D是CB的中点，则AD=____cm
4.有A、B、C三城市，已知A、B两市的距离为50千米，B、C两市的距离是30千米，那么A、C两市间的距离是（ ） （A）80千米 （B）20千米 （C）40千米 （D）处于20千米～80千米之间
如图是一个四边形，现在取各边的中点并连接成四边形，想一想得到的四边形与原四边形，哪一个的周长大？如是在各边任意取一点呢？
1、线段的基本性质：两点之间线段最短。
两点之间的距离：两点之间线段的长度。
3、线段的两种比较方法：叠合法和度量法。
4、线段的中点的概念及表示方法。
2、尺规作图：作一条线段等于已知线段。