初中数学冀教版七年级下册第十一章 因式分解11.2 提公因式法教学演示课件ppt

这是一份初中数学冀教版七年级下册第十一章 因式分解11.2 提公因式法教学演示课件ppt，共18页。PPT课件主要包含了学习目标，问题引入，mambmc，有为m，abab，相同因式p，pa+pb+pc，系数最大公约数，字母相同的字母，所以公因式是3x等内容，欢迎下载使用。

1.能确定多项式的公因式.（重、难点）2.能熟练运用提公因式法把多项式因式分解.(重点）
问题1：多项式ma+mb+mc有哪几项？
问题2：每一项的因式都分别有哪些？
问题3：这些项中有没有公共的因式，若有，公共的因 式是什么？
依次为m, a和m, b和m, c
问题4：请说出多项式ab2-2a2b中各项的公共的因式.
这个多项式有什么特点？
一般地，多项式的各项都含有的因式，叫做这个多项式各项的公因式，简称多项式的公因式.
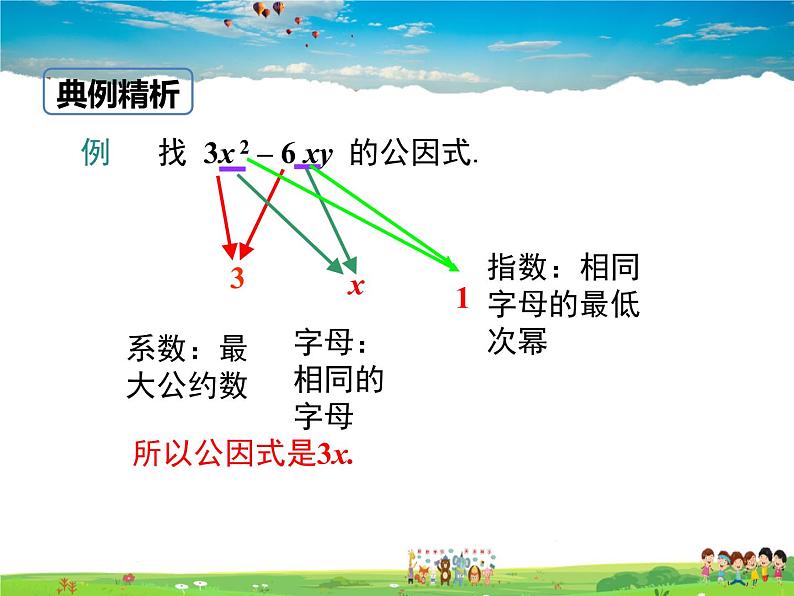
例 找 3x 2 – 6 xy 的公因式.
指数：相同字母的最低次幂
正确找出多项式各项公因式的关键是：
1.定系数：公因式的系数是多项式各项系数的最大公 约数. 2.定字母：字母取多项式各项中都含有的相同的字母. 3.定指数：相同字母的指数取各项中最小的一个，即 字母最低次幂.
写出下列多项式的公因式.（1）x-x2； （2）abc+2a；（3）abc-b2+2ab； （4）a2+ax2；
问题：ma+mb+mc=m( ) ab2-2a2b=ab( ) (提示，逆用乘法分配律）
逆用乘法对加法的分配律，可以把公因式写在括号外边，作为积的一个因式，这种将多项式分解因式的方法，叫做提公因式法.
思考：以下是三名同学对多项式2x2+4x分解因式的结果： （1）2x2+4x = 2(x2+2x)； （2）2x2+4x = x(2x+4)； （3） 2x2+4x = 2x(x+2). 第几位同学的结果是正确的？
用提公因式法分解因式应注意哪些问题呢？
做乘法运算来检验易得第3位同学的结果是正确的.
例2：把下列多项式分解因式： (1)-3x2+6xy-3xz； (2)3a3b+9a2b2-6a2b.
解：(1) -3x2+6xy-3xz=(-3x)·x+(-3x)·(-2y)+(-3x)·z =-3x·(x-2y+z).
方法归纳：用提公因式法分解因式应注意：(1)如果多项式的第一项系数是负数,一般要先提出负因数，保证括号内首项为正.(2)公因式的系数是负号时，提公因式后各项要变号.
(2)3a3b+9a2b2-6a2b=3a2b·a+3a2b·3b-3a2b·2 =3a2b(a+3b-2)
例3：把分解因式：2a(b+c)-5(b+c).
解：2a(b+c)-5(b+c) =(b+c)·2a+(b+c)·5 =(b+c)(2a-5).
方法归纳：公因式可以是数字，字母，单项式，还可以是多项式.
提公因式法步骤（分两步）： 第一步:找出公因式； 第二步:提取公因式 ，即将多项式化为两个因式的乘积.
注意：公因式既可以是一个单项式的形式，也可以是一个多项式的形式.
运用提公因式法分解因式常常运用到整体思想，整体思想是数学中一种重要而且常用的思想方法.
1. 下列多项式：4a2b（a﹣b）﹣6ab2（b﹣a）中，各项的公因式是（　　）A．4ab B．2abC．ab（a﹣b） D．2ab（a﹣b）
2. 多项式8xmyn﹣1﹣12x3myn的公因式是（　　）A．xmynB．xmyn﹣1C．4xmynD．4xmyn﹣1
解析：（1）公因式的系数是多项式各项系数的最大 公约数，为4； （2）字母取各项都含有的相同字母，为xy； （3）相同字母的指数取次数最低的，x为m次， y为n-1次； 多项式的公因式是4xmyn﹣1．
3. 把多项式﹣4a3+4a2﹣16a分解因式（　　）A．﹣a（4a2﹣4a+16）B．a（﹣4a2+4a﹣16）C．﹣4（a3﹣a2+4a）D．﹣4a（a2﹣a+4）
4. 若ab=﹣3，a﹣2b=5，则a2b﹣2ab2的值是（　　）A．﹣15 B．15 C．2 D．﹣8
解析：因为ab=﹣3，a﹣2b=5， 所以a2b﹣2ab2=ab（a﹣2b） =﹣3×5=﹣15．
5. 计算（﹣3）m+2×（﹣3）m﹣1，得（　　）A．3m﹣1 B．（﹣3）m﹣1C．﹣（﹣3）m﹣1 D．（﹣3）m
解析：（﹣3）m+2×（﹣3）m﹣1 =（﹣3）m﹣1（﹣3+2） =﹣（﹣3）m﹣1．