九年级下册29.4 切线长定理教学课件ppt

这是一份九年级下册29.4 切线长定理教学课件ppt，共20页。PPT课件主要包含了学习目标，¤切线长的定义，∴PAPB，∠OPA∠OPB，¤切线长定理，¤几何语言，2连接两切点，⊙O就是所求的圆，填一填，三角形外接圆的圆心等内容，欢迎下载使用。

1.掌握切线长定理，初步学会运用切线长定理进行计算 与证明.（重点）2.了解有关三角形的内切圆和三角形的内心的概念.3.学会利用方程思想解决几何问题，体验数形结合思想.（难点）
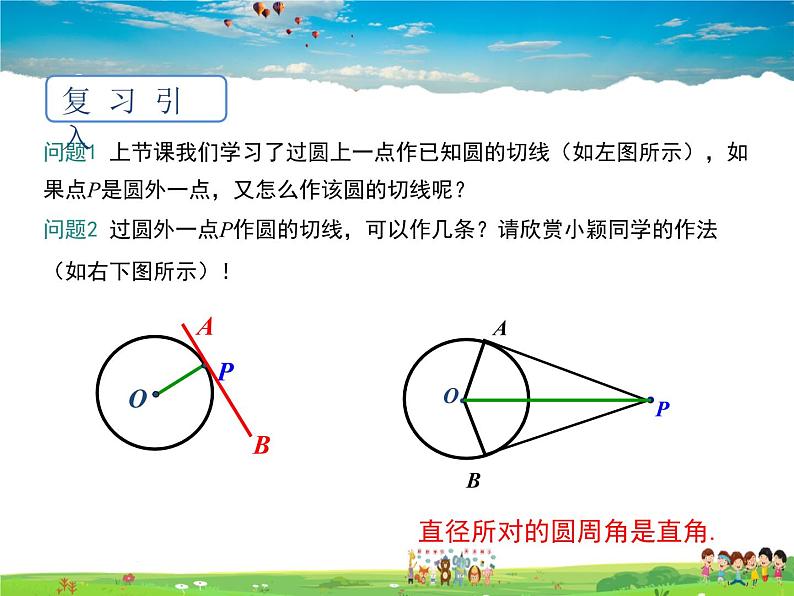
问题1 上节课我们学习了过圆上一点作已知圆的切线（如左图所示），如果点P是圆外一点，又怎么作该圆的切线呢？问题2 过圆外一点P作圆的切线，可以作几条？请欣赏小颖同学的作法（如右下图所示）！
直径所对的圆周角是直角.
过圆外一点画圆的切线，这点和切点之间的线段长叫做这点到圆的切线长．
①切线是直线，不能度量.
¤ 切线长与切线的区别
②切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量．
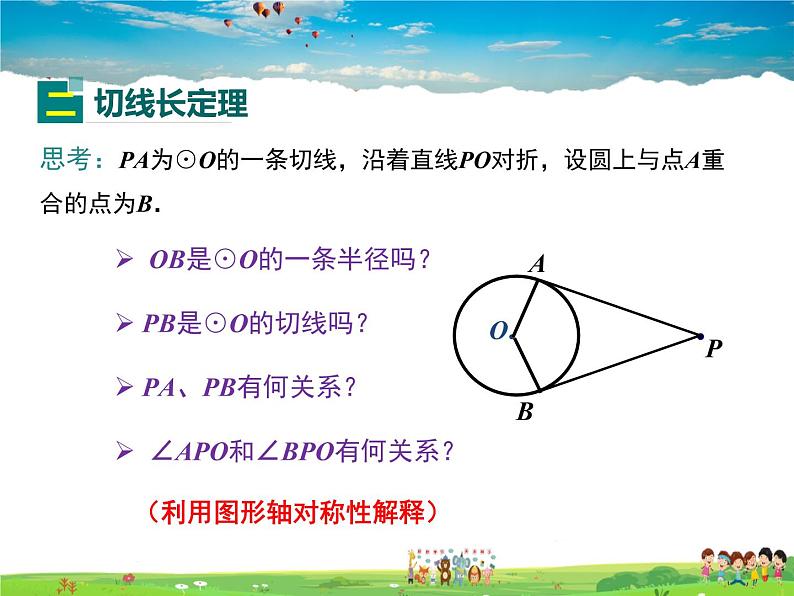
思考：PA为⊙O的一条切线，沿着直线PO对折，设圆上与点A重合的点为B．
OB是⊙O的一条半径吗？
PB是⊙O的切线吗？
（利用图形轴对称性解释）
PA、PB有何关系？
∠APO和∠BPO有何关系？
过圆外一点所画的圆的两条切线的切线长相等.
∵PA，PB分别切⊙O于A，B
★切线长定理为证明线段相等、角相等提供了新的方法.
问题：PA，PB是⊙O的两条切线，A，B为切点，直线OP交⊙O于点D，E，交AB于C.
（1）写出图中所有的垂直关系：
OA⊥PA，OB ⊥PB，AB ⊥OP.
（3）写出图中所有的全等三角形：
△AOP≌ △BOP， △AOC≌ △BOC， △ACP≌ △BCP.
（4）写出图中所有的等腰三角形：
△ABP ， AOB.
（2）写出图中与∠OAC相等的角：
∠OAC=∠OBC=∠APC=∠BPC.
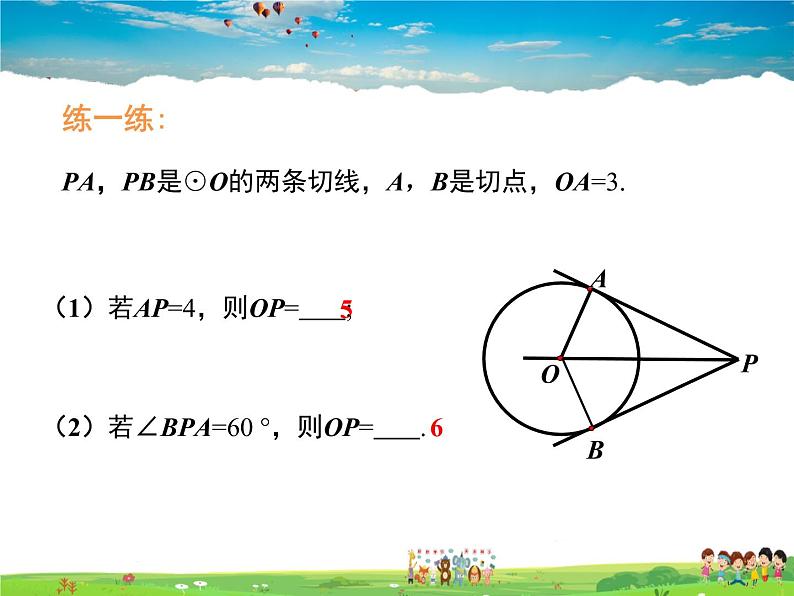
练一练: PA，PB是⊙O的两条切线，A，B是切点，OA=3.
（1）若AP=4，则OP= ;
（2）若∠BPA=60 °，则OP= .
（3）连接圆心和圆外一点.
（1）分别连接圆心和切点；
问题1 一张三角形的铁皮，如何在它上面截下一块圆形的用料，使截出的圆与三角形各边都相切呢？
问题2 如何作圆，使它和已知三角形的各边都相切？
已知：△ABC.求作：和△ABC的各边都相切的圆.
作法：1.作∠B和∠C的平分线BM和CN，交点为O.2.过点O作OD⊥BC.垂足为D.3.以O为圆心，OD为半径作圆O.
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.三角形的内心到三角形的三边的距离相等.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
点O是△ABC的内切圆，点O是△ABC的内心，△ABC是⊙O的外切三角形.
1.OA=OB=OC2.外心不一定在三角形的内部
1.到三边的距离相等2.OA，OB，OC分别平分∠BAC，∠ABC，∠ACB3.内心在三角形内部
三角形三边中垂线的交点
三角形三条角平分线的交点
例2 △ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=13cm，BC=14cm，CA=9cm，求AF，BD，CE的长.
设AF=xcm，则AE=xcm.
∴CE=CD=AC－AE=9-x(cm)， BF=BD=AB－AF=13-x(cm).
由 BD+CD=BC，可得 (13-x)+(9-x)=14，
∴ AF=4(cm)，BD=9(cm)，CE=5(cm).
想一想：图中你能找出哪些相等的线段？理由是什么？
方法小结：关键是熟练运用切线长定理，将相等线段转化集中到某条边上，从而建立方程.
2.如图，已知点O是△ABC 的内心，且∠ABC＝ 60°，∠ACB＝80°，则∠BOC＝ .
1.如图，PA，PB是⊙O的两条切线，切点分别是A，B，如果AP＝4，∠APB＝40°，则∠APO＝ ，PB＝ .
3.如图，PA，PB是⊙O的两条切线，切点为A，B，∠P＝ 50°，点C是⊙O上异于A，B的点，则∠ACB= .
4.△ABC的内切圆⊙O与三边分别切于D，E，F三点，如图，已知AF＝3，BD+CE＝12，则△ABC的周长是 .
直角三角形的两直角边分别是3cm ,4cm,试问：（1）它的外接圆半径是 cm;内切圆半 径是 cm？
解：如图，△ABC的外接圆直径为AB.由勾股定理可得AB=5cm，故外接圆半径为2.5cm.连接AO，BO，CO.设△ABC的内接圆半径为r.由面积公式可得：S△ABC=S△AB+S△AC+S△BC ，即 ，所以 ，代入数据得r=1cm.
方法小结：直角三角形的外接圆半径等于斜边长的一半，内接圆半径 .
（2）若移动点O的位置，使⊙O保持与△ABC的边 AC，BC都相切，求⊙O的半径r的取值范围.
解：如图所示，设与BC，AC相切的最大圆与BC，AC的切点分别为B，D,连接OB，OD,则四边形BODC为正方形.
∴半径r的取值范围为0＜r≤3.