初中数学8.1 同底数幂的乘法集体备课ppt课件

这是一份初中数学8.1 同底数幂的乘法集体备课ppt课件，共37页。PPT课件主要包含了课堂讲解，课时流程，知识点，同底数幂的乘法法则，xy＝z，知识小结，易错小结等内容，欢迎下载使用。

同底数幂的乘法法则同底数幂的乘法法则的应用
1. ①什么叫乘方? ②乘方的结果叫做什么?(1) 2×2 ×2=2( )(2) a·a·a·a·a = a( ) (3) a·a·…·a = a( )
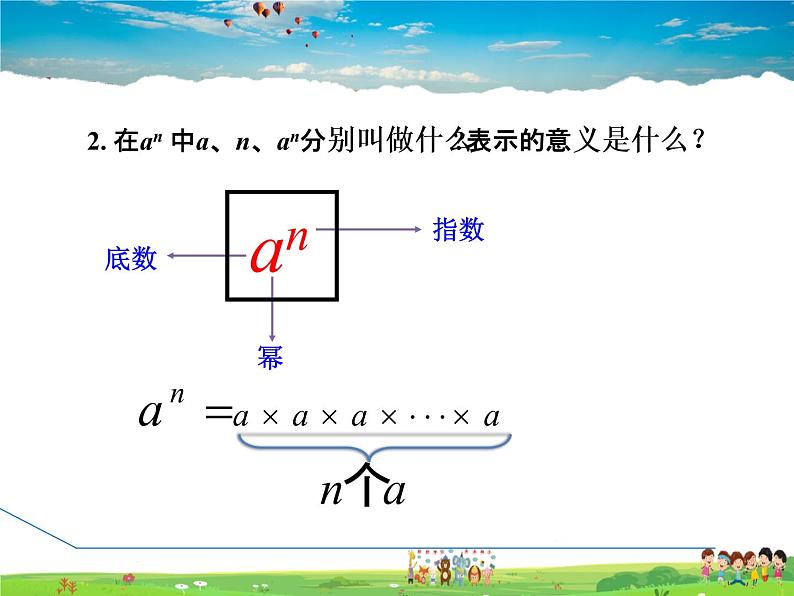
2. 在an 中a、n、an分别叫做什么?表示的意义是什么？
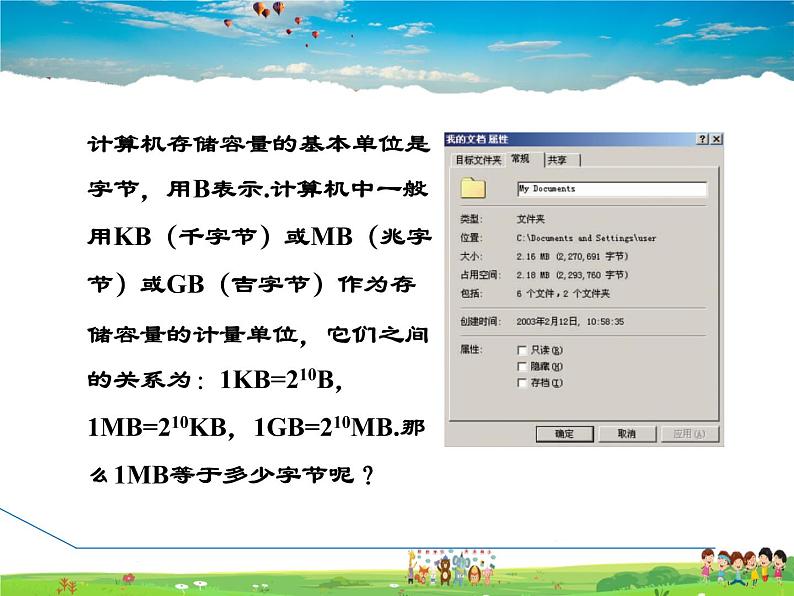
计算机存储容量的基本单位是字节，用B表示.计算机中一般用KB（千字节）或MB（兆字节）或GB（吉字节）作为存储容量的计量单位，它们之间的关系为：1KB=210B，1MB=210KB，1GB=210MB.那么1MB等于多少字节呢？
回顾乘方的意义：23=2×2×2, 24=2×2×2×2.1. 用幂表示下列各式的结果：(1) 24×23=________；(2) 210×210=________；(3) ________；(4) a2·a3= ________；
2. 通过上面的计算.关于两个同底数幂相乘的结果，你发现了什么规律？3. 若m，n是正整数，根据你发现的规律，用幂的形式表示am·an .一般地，对于正整数m，n，有am·an=(a·a· … ·a)(a·a· … ·a)= a·a· … ·a=a m+n .
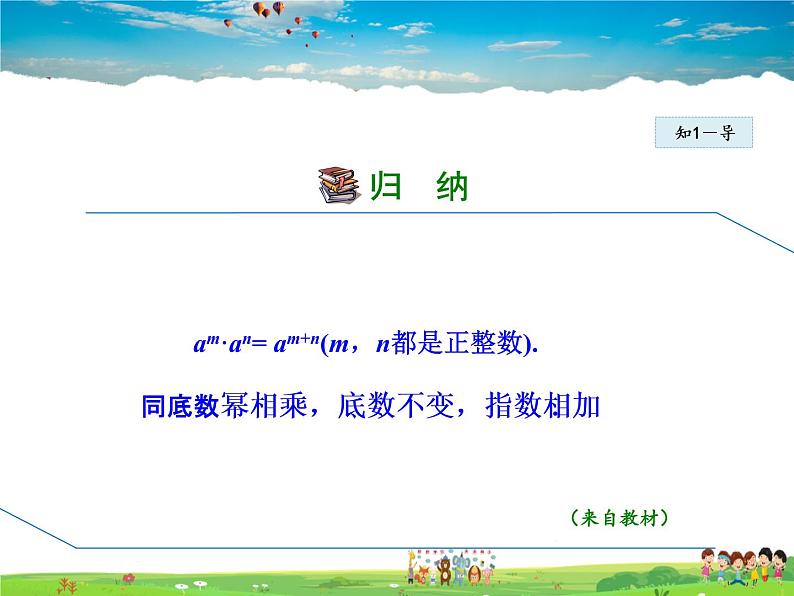
am·an= am+n(m，n都是正整数).同底数幂相乘，底数不变，指数相加.
(1)同底数幂的乘法法则只有在底数相同时才能使用， 并且底数不变，指数相加，而不是指数相乘．(2)不同底数要先化成同底数．(3)单个字母或数可以看作指数为1的幂，参与同底数 幂的运算时，不能忽略了幂指数1.
把下列各式表示成幂的形式：(1) 26×23； (2) a2·a4；(3) xm·xm+1； (4) a·a2·a3.
(1) 26×23=26+3=29 . (2) a2·a4= a2+4 =a6 .(3) xm·xm+1 = xm+(m+1)=x2m+1.(4) a·a2·a3 = a1+2+3 =a6.
同底数幂相乘，首先确定符号，负因数出现奇数个就取负号，出现偶数个就取正号，然后按照同底数幂的乘法法则进行计算．
下列各式的计算是否正确？如果不正确. 请改正过来.(1) a2·a3 =a5. (2) b·b=2b. (3) a·a3 =a3. (4) a3·a4 =a12.
(1)正确．(2)不正确，应为b·b＝b2.(3)不正确，应为a·a3＝a4.(4)不正确，应为a3·a4＝a7.
(1)105×104＝105＋4＝109.(2)(3)(－2)2·(－2)5＝(－2)2＋5＝(－2)7＝－27.　(4)b2·b4·b5＝b2＋4＋5＝b11.
计算：(1) 105×104； (2) (3) (－2)2·(－2)5 ； (4) b2·b4·b5.
计算下列各题，结果用幂的形式表示.(1)104×107； (2)26×25；(3) ； (4) ；(5)(－3)3×(－3)4 ； 　(6)(－7)2×(－7)4；
(1)104×107＝104＋7＝1011.(2)26×25＝26＋5＝211.(3)(4)(5)(－3)3×(－3)4＝(－3)3＋4＝(－3)7＝－37.　(6)(－7)2×(－7)4＝(－7)2＋4＝(－7)6＝76.
计算：(1) x4·x8； (2) －d·d3；(3) am·an＋1； (4) a·a3·a5.　
(1) x4·x8＝x4＋8＝x12.(2) －d·d3＝－d1＋3＝－d4.(3) am·an＋1＝am＋n＋1.(4) a·a3·a5＝a1＋3＋5＝a9.　
计算：(1) a2·an·an＋1 ； (2) xm·xm＋1·xm＋2 . 　
(1) a2·an·an＋1＝a2＋n＋n＋1＝a2n＋3.(2) xm·xm＋1·xm＋2＝xm＋m＋1＋m＋2＝x3m＋3.
下列各式中是同底数幂的是(　　)A．23与32 B．a3与(－a)3C．(m－n)5与(m－n)6 D．(a－b)2与(b－a)3【中考·连云港】计算a·a2的结果是(　　)A．a B．a2 C．2a2 D．a3
【中考·呼伦贝尔】化简(－x)3(－x)2，结果正确的是(　　)A．－x6 B．x6 C．x5 D．－x5计算(－y2)·y3的结果是(　　)A．y5 B．－y5 C．y6 D．－y6
计算：(1)(x－y)3·(y－x)5；(2)(x－y)3·(x－y)2·(y－x)；(3)(a－b)3·(b－a)4.
先将不是同底数的幂转化为同底数的幂，再运用法则计算．
(1)(x－y)3·(y－x)5＝(x－y)3·[－(x－y)5]＝－(x－y)3＋5＝－(x－y)8.(2)(x－y)3·(x－y)2·(y－x)＝(x－y)3·(x－y)2·[－(x－y)]＝－(x－y)3＋2＋1＝－(x－y)6.(3)(a－b)3·(b－a)4＝(a－b)3·(a－b)4＝(a－b)3＋4＝(a－b)7.
底数互为相反数的幂相乘时，可以利用幂确定符号的方法先转化为同底数幂，再按法则计算，统一底数时尽可能地改变偶次幂的底数，这样可以减少符号的变化．
(1)将(a＋b)2·(a＋b)3表示成以a＋b为底的幂.(2)将(x－y)4·(y－x)3表示成以x－y为底的幂.
(1)(a＋b)2·(a＋b)3＝(a＋b)2＋3＝(a＋b)5.(2)(x－y)4·(y－x)3＝(x－y)4·[－(x－y)3]＝－(x－y)4＋3＝－(x－y)7.
下列各式能用同底数幂的乘法法则进行计算的是(　　)A．(x＋y)2·(x－y)3 B．(－x－y)·(x＋y)2 C．(x＋y)2＋(x＋y)3 D．－(x－y)2·(－x－y)3
【中考·福州】下列算式中，结果等于a6的是(　　)A．a4＋a2 B．a2＋a2＋a2C．a2·a3 D．a2·a2·a2若a·a3·am＝a8，则m＝________.
用幂的形式表示结果：(x－y)2·(y－x)3＝_____________________．【中考·安徽】按一定规律排列的一列数：21，22，23，25，28，213，…，若x，y，z表示这列数中的连续三个数，猜想x，y，z满足的关系式是________．
－(x－y)5(或(y－x)5)
同底数幂的乘法法则应用
太阳系的形状像一个以太阳为中心的大圆盘，光通过这个圆盘半径的时间约为2×104 s，光的速度约为3×105 km/s.求太阳系的直径.
2×3×105×2×104= 12×109(km).答：太阳系的直径约为12×109 km.
用科学计数法表示的两个数相乘时，常把10n看作底数相同的幂参与运算，而把其他部分看作常数参与运算，然后把两者再相乘或直接表示为科学计数法的形式.
用幂的形式表示下列问题的结果： (1)2个棱长为2 cm的正方体的体积的和是_____cm3. (2)9个棱长为3 cm的正方体的体枳的和是_____cm3.
地球的质量约为5.98×1024kg，太阳质量是地球质量的3. 3×105倍.求太阳的质量.
根据题意，得5.98×1024×3.3×105＝19.734×1029＝1.973 4×1030(kg)．答：太阳的质量约为1.973 4×1030 kg.
计算：(1)x·x2·x3＋x2·x4； (2)x2·x5－x·x2·x4.
(1)x·x2·x3＋x2·x4＝x1＋2＋3＋x2＋4＝x6＋x6＝2x6.(2)x2·x5－x·x2·x4＝x2＋5－x1＋2＋4＝x7－x7＝0.
设n是正整数，计算：(1)2n＋1－2n ； (2)4×5n－5n＋1.
(1)2n＋1－2n＝2×2n－2n＝2n.(2)4×5n－5n＋1＝4×5n－5×5n＝－5n.
【中考·大庆】若am＝2，an＝8，则am＋n＝________.计算(a＋b)3·(a＋b)2m·(a＋b)n的结果为(　　)A．(a＋b)6m＋n B．(a＋b)2m＋n＋3C．(a＋b)2mn＋3 D．(a＋b)6mnx3m＋3可以写成(　　)A．3xm＋1 B．x3m＋x3 C．x3·xm＋1 D．x3m·x3
计算(－2)2 019＋(－2)2 018的结果是(　　)A．－22 018 B．22 018 C．－22 019 D．22 019一个长方形的长是4.2×104cm，宽是2×104cm，求此长方形的面积．
长方形的面积＝长×宽＝4.2×104×2×104＝8.4×108(cm2)．所以长方形的面积为8.4×108cm2.
已知2x＝5，2y＝7，2z＝35.试说明：x＋y＝z.
因为2x＝5，2y＝7，2z＝35，所以2x·2y＝5×7＝35＝2z.所以2x·2y＝2x＋y＝2z，即2x＋y＝2z.所以x＋y＝z.
1. 运用同底数幂的乘法法则时，注意成立的条件是底 数相同．遇到底数不同的情况可以通过变换转化为 底数相同的，然后运用法则进行计算．2. 同底数幂的乘法法则对三个或三个以上的同底数幂 的乘法同样适用，底数可以是单项式，也可以是多 项式．3. 同底数幂的乘法法则可以正用，也可以逆用，am＋n ＝am·an (m，n都是正整数)．
请分析以下解答过程是否正确，如不正确，请写出正确的解答过程．计算：(1)x·x3；(2)(－x)2·(－x)4；(3)x4·x3.解：(1)x·x3＝x0＋3＝x3.(2)(－x)2·(－x)4＝(－x)6＝－x6.(3)x4·x3＝x4×3＝x12.
易错点：对法则理解不透导致错误
(1)(2)(3)的解答过程均不正确，正确的解答过程如下：(1)x·x3＝x1＋3＝x4.(2)(－x)2·(－x)4＝(－x)2＋4＝(－x)6＝x6.(3)x4·x3＝x4＋3＝x7.
(1)x的指数是1时省略不写，误以为指数是0；(2)幂的符号错误，积的符号应为正；(3)同底数幂相乘，底数不变，指数相加，误以为指数相乘.