初中数学冀教版七年级下册8.4 整式的乘法教案配套ppt课件

这是一份初中数学冀教版七年级下册8.4 整式的乘法教案配套ppt课件，共34页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，x2＋5x＋6，知识小结，易错小结等内容，欢迎下载使用。

多项式与多项式的乘法法则多项式与多项式的乘法法则的应用
某地区在退耕还林期间，有一块原长a米、宽n米的长方形林区增长了m米，加宽了b米，扩大后的林区面积是多少？
多项式与多项式相乘的法则
利用如下的长方形卡片拼成更大的长方形(每种卡片有若干张).
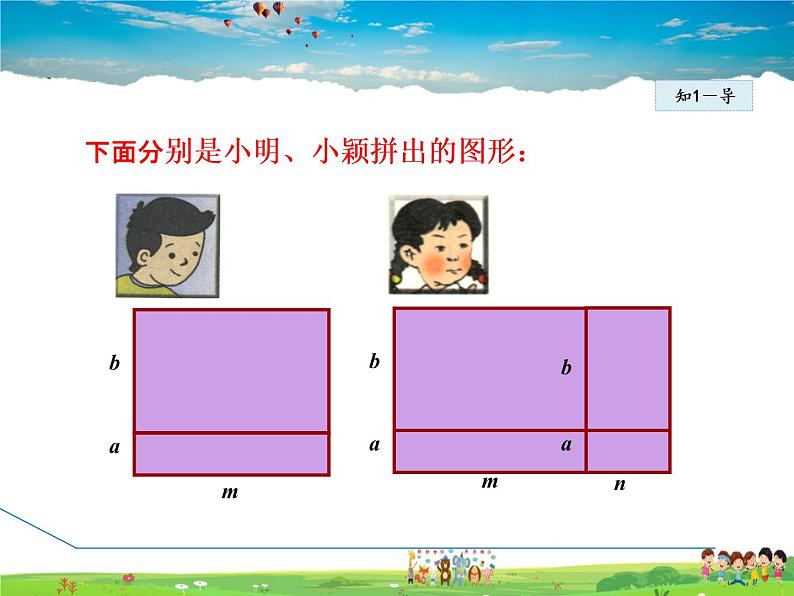
下面分别是小明、小颖拼出的图形：
(1)用不同的形式表示小明所拼长方形的面积， 并进行比较。m(a+b)=ma+mb(2)用不同的形式表示小颖所拼长方形的面积，并进行比较。(m+n)(a+b)=m(a+b)+n(a+b)还可以看成是四个小长方形的组合，其面积是= ma+mb+na+nb
多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加．
(1)该法则的本质是将多项式乘以多项式最终转化为几 个单项式乘积的和的形式． (2)多项式乘以多项式，结果仍为多项式，但通常有同 类项合并，在合并同类项之前，积的项数应等于两 个多项式的项数之积．
计算：(1) (x－2)(x+1) ；(2) (3a－2) .
(1) (x－2)(x+1) ＝ x2+x－2x－2＝ x2－x－2.(2) (3a－2) ＝a2－ a－6a+4＝a2－ a+4.
多项式与多项式相乘，为了做到不重不漏，可以用“箭头法”标注求解，如计算 时，可在草稿纸上作如下标注： 根据箭头指示，即可得到 ，把各项相加，继续求解即可．
计算：(1)(x＋2)(2x－4)； (2)(x＋2y)(3a＋4b).
(1)(x＋2)(2x－4)＝x·2x－4x＋2×2x－2×4＝2x2－4x＋4x－8＝2x2－8.　(2)(x＋2y)(3a＋4b)＝x·3a＋x·4b＋2y·3a＋2y·4b＝3ax＋4bx＋6ay＋8by.
计算：(1)(x－1)(x－2) ； (2)(x＋3)(x－4) ；(3)(3x＋4)(2x－1) ； (4)(x＋y)(2a－b).
(1)(x－1)(x－2)＝x2－2x－x＋2＝x2－3x＋2.(2)(x＋3)(x－4)＝x2－4x＋3x－12＝x2－x－12.(3)(3x＋4)(2x－1)＝6x2－3x＋8x－4＝6x2＋5x－4.(4)(x＋y)(2a－b)＝2ax－bx＋2ay－by.
计算：(1)(x＋y)(2x－3y) ； (2)(4x－3y)(y＋4x) ；(3)(x＋y)2 ； (4)(a＋m)(a－m).
(1)(x＋y)(2x－3y)＝2x2－3xy＋2xy－3y2＝2x2－xy－3y2.(2)(4x－3y)(y＋4x)＝4xy＋16x2－3y2－12xy＝16x2－8xy－3y2.(3)(x＋y)2＝(x＋y)(x＋y)＝x2＋xy＋xy＋y2＝x2＋2xy＋y2.(4)(a＋m)(a－m)＝a2－am＋am－m2＝a2－m2.
【中考·武汉】计算(x＋1)(x＋2)的结果为(　　)A．x2＋2 B．x2＋3x＋2C．x2＋3x＋3 D．x2＋2x＋2下列多项式相乘结果为a2－3a－18的是(　　)A．(a－2)(a＋9) B．(a＋2)(a－9)C．(a＋3)(a－6)　　 D．(a－3)(a＋6)
计算：(1) (x+3y)(2x－y) ；(2) (－3x+2b)(2x－4b) .
(1) (x+3y)(2x－y) ＝ 2x2－xy+6xy－3y2＝ 2x2+5xy－3y2.(2) (－3x+2b)(2x－4b) ＝－6x2+12bx+4bx－8b2＝－6x2+16bx－8b2.
计算：(1)(a－1)(a－2)－a(a－5)；(2)3x(x＋2)－(x＋1)(3x－4).
(1)(a－1)(a－2)－a(a－5)＝a2－2a－a＋2－a2＋5a＝2a＋2.(2)3x(x＋2)－(x＋1)(3x－4)＝3x2＋6x－(3x2－4x＋3x－4)＝3x2＋6x－3x2＋x＋4＝7x＋4.
解方程：(1)6x(x－2)－(x－2)(3x－1)＝3x2－8 ；(2)(x－2)(2x－5)－2(x－1)(x＋1)＝3.
(1)6x(x－2)－(x－2)(3x－1)＝3x2－8，6x2－12x－(3x2－x－6x＋2)＝3x2－8，6x2－12x－3x2＋7x－2－3x2＋8＝0，－5x＋6＝0，5x＝6，x＝ .
(2)(x－2)(2x－5)－2(x－1)(x＋1)＝3，2x2－5x－4x＋10－2(x2＋x－x－1)＝3，2x2－9x＋10－2x2＋2－3＝0，－9x＋9＝0，9x＝9，x＝1.
计算：(1)(a＋b)(a2－ab＋b2) ；(2)(a－b)(a2＋ab＋b2).
(1)(a＋b)(a2－ab＋b2)＝a3－a2b＋ab2＋a2b－ab2＋b3＝a3＋b3.(2)(a－b)(a2＋ab＋b2)＝a3＋a2b＋ab2－a2b－ab2－b3＝a3－b3.
计算(x－a)(x2＋ax＋a2)的结果是(　　)A．x3－2ax2－a3 B．x3－a3C．x3＋2a2x－a3 D．x3＋2ax2－2a2x＋a3下列各式中错误的是(　　)A．(2a＋3)(2a－3)＝4a2－9B．(3a＋4b)2＝9a2＋24ab＋4b2C．(x＋2)(x－10)＝x2－8x－20D．(x＋y)(x2－xy＋y2)＝x3＋y3
已知M，N分别是二次多项式和三次多项式，则M×N(　　)A．一定是五次多项式B．一定是六次多项式C．一定是不高于五次的多项式D．无法确定积的次数
多项式与多项式的乘法法则的应用
先化简，再求值：(x－2y)(x＋3y)－(2x－y)(x－4y)，其中：x＝－1，y＝2.
先分别将两组多项式相乘，并将第二个多项式乘以多项式的结果先用括号括起来，再去括号，最后再合并同类项．
原式＝x2＋3xy－2xy－6y2－(2x2－8xy－xy＋4y2)＝x2＋xy－6y2－(2x2－9xy＋4y2)＝x2＋xy－6y2－2x2＋9xy－4y2＝－x2＋10xy－10y2.当x＝－1，y＝2时，原式＝－(－1)2＋10×(－1)×2－10×22＝－61.
多项式乘法与加减相结合的混合运算，通常先算出相乘的结果，再进行加减运算，运算中特别要注意括号的运用和符号的变化，当两个多项式相减时，后一个多项式通常用括号括起来，这样可以避免运算结果出错．
先化简，再求值： 5x(2x＋1)－(2x＋3)(5x－1).其中，x=13.
5x(2x＋1)－(2x＋3)(5x－1)＝10x2＋5x－(2x·5x－2x＋15x－3)＝10x2＋5x－10x2－13x＋3＝3－8x.当x＝13时，原式＝3－8×13＝3－104＝－101.
计算： (1)(a＋b)3； (2)(a－b)3.
(1)(a＋b)3＝(a＋b)(a＋b)(a＋b)＝(a2＋ab＋ab＋b2)(a＋b)＝(a2＋2ab＋b2)(a＋b)＝a3＋2a2b＋ab2＋a2b＋2ab2＋b3＝a3＋3a2b＋3ab2＋b3.(2)(a－b)3＝(a－b)(a－b)(a－b)＝(a2－ab－ab＋b2)(a－b)＝(a2－2ab＋b2)(a－b)＝a3－2a2b＋ab2－a2b＋2ab2－b3＝a3－3a2b＋3ab2－b3.
若(x－1)(x＋3)＝x2＋mx＋n，则m，n的值分别是(　　)A．m＝1，n＝3 B．m＝2，n＝－3C．m＝4，n＝5 D．m＝－2，n＝3【中考·佛山】若(x＋2)(x－1)＝x2＋mx＋n，则m＋n＝(　　)A．1 B．－2 C．－1 D．2
若(x＋a)(x－2)的积中不含x项，那么a的值为(　　)A．2　　 B．－2　　 C. D．－【中考·连云港】已知m＋n＝mn，则(m－1)·(n－1)＝______．
【中考·吉林】如图，长方形ABCD的面积为________________．(用含x的式子表示)已知(x－2)(1－kx)－(2x－3)(2x＋3)的结果中不含有x的一次式，则k＝________．
计算：(1)(－7x2－8y2)(－x2＋3y2)；(2)【中考·镇江】x(x＋1)－(x＋1)(x－2)．
(1)原式＝7x4－21x2y2＋8x2y2－24y4＝7x4－13x2y2－24y4.(2)原式＝x2＋x－(x2－2x＋x－2)＝x2＋x－x2＋2x－x＋2＝2x＋2.
【中考·宜昌】先化简，再求值： 4x·x＋(2x－1)(1－2x)．其中x＝ .
4x·x＋(2x－1)(1－2x)＝4x2＋(2x－4x2－1＋2x)＝4x2＋4x－4x2－1＝4x－1.当x＝ 时，原式＝4× －1＝－ .
1. 多项式乘以多项式的 依据是什么？2. 如何进行多项式与多项式乘法运算？ 3. 运用多项式乘法法则，要有序地逐项相乘，不要 漏乘，并注意项的符号． 最后的计算结果要化简——合并同类项.
计算：3(2x－1)(x＋6)－5(x－3)(x＋6)．
易错点：多项式与多项式相乘易漏乘或误判符号导致出错
原式＝3(2x2＋12x－x－6)－5(x2＋6x－3x－18)＝6x2＋33x－18－5x2－15x＋90＝x2＋18x＋72.