初中数学冀教版九年级下册30.2 二次函数的图像和性质课文ppt课件

这是一份初中数学冀教版九年级下册30.2 二次函数的图像和性质课文ppt课件，共32页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，回顾旧知，知识点，想一想，1列表，2描点等内容，欢迎下载使用。

二次函数y=ax2的图像 二次函数y=ax2的性质
(1)一次函数的图象是什么？ 一条直线 (2)画函数图象的基本方法与步骤是什么？ 列表——描点——连线(3)研究函数时，主要用什么来了解函数的性质呢？ 主要工具是函数的图象
二次函数y=ax2的图像
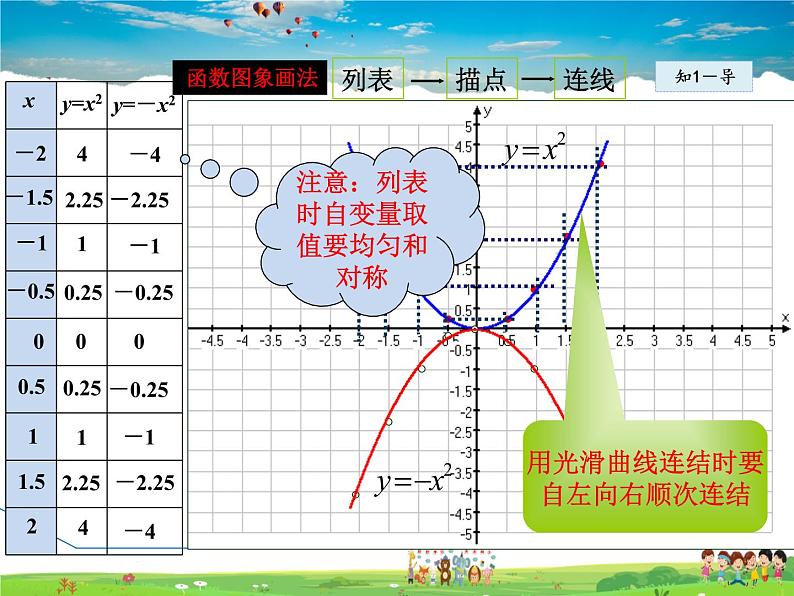
　　在同一直角坐标系中，画出函数y = x2 和y =－x2 的图象，这两个函数的图象相比， 有什么共同点？有什么不同点？
注意：列表时自变量取值要均匀和对称
用光滑曲线连结时要自左向右顺次连结
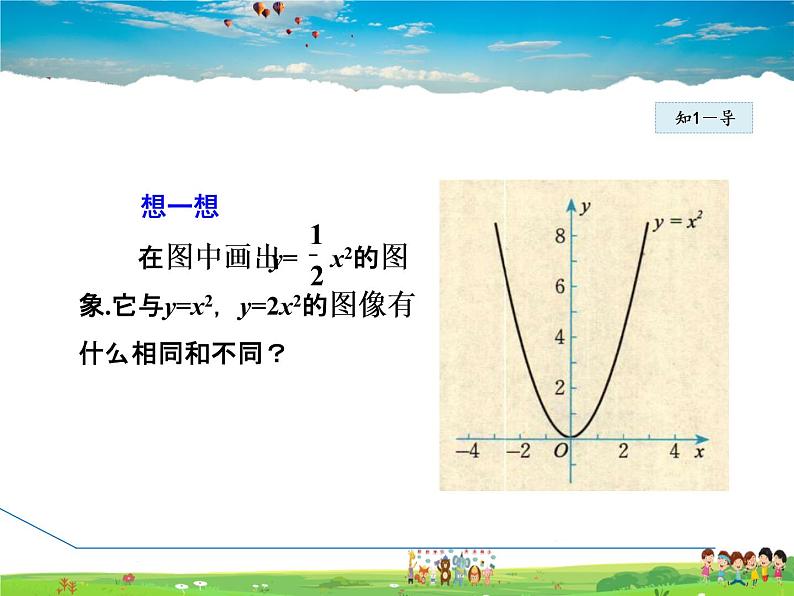
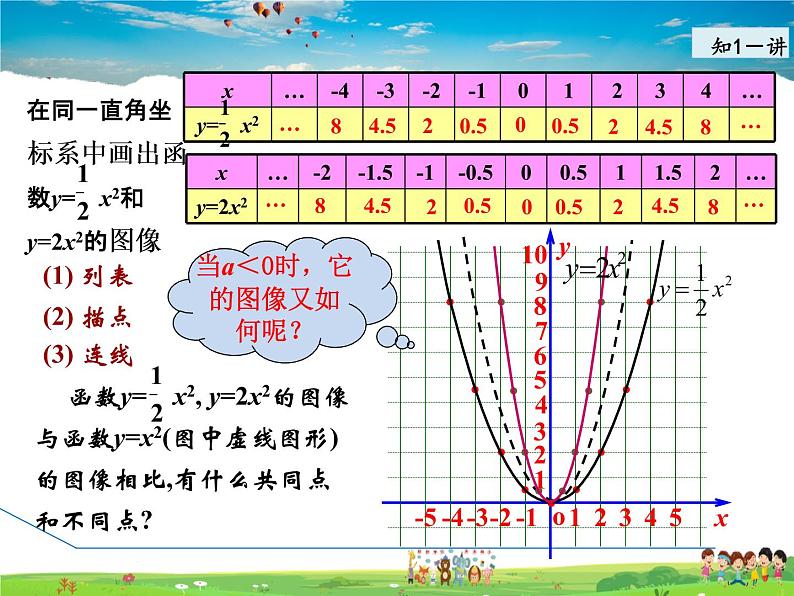
在同一直角坐标系中画出函数y= x2和y=2x2的图像
函数y= x2, y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点?
当a＜0时，它的图像又如何呢？
一般地，抛物线y=ax2的对称轴是y轴，顶点是原点.
当a>0时，抛物线的开口向上，顶点是抛物线的最低点，a越大，抛物线的开口越小；
当a<0时，抛物线的开口向下，顶点是抛物线的最高点，a越大，抛物线的开口越大.
例1 在同一坐标系中画出y1＝2x2，y2＝－2x2和 y3＝ x2的图像，正确的是图中的(　　)
当x＝1时, y1, y2, y3的图像上的对应点分别是(1, 2),(1, －2), (1， ), 可知, 其中有两点在第一象限, 一点在第四象限, 排除B, C；在第一象限内, y1的对应点(1, 2)在上, y3的对应点(1， )在下, 排除A.
1 关于二次函数y＝3x2的图像，下列说法错误的是(　　) A．它是一条抛物线 B．它的开口向上，且关于y轴对称 C．它的顶点是抛物线的最高点 D．它与y＝－3x2的图像关于x轴对称
2 关于二次函数y＝2x2与y＝－2x2，下列叙述正确的有 (　　) ①它们的图像都是抛物线；②它们的图像的对称轴都 是 y轴；③它们的图像都经过点(0，0)；④二次函数 y ＝2x2的图像开口向上，二次函数y＝－2x2的图像开口 向下；⑤它们的图像关于x轴对称． A．5个 B．4个 C．3个 D．2个
(中考·丽水)若二次函数y＝ax2的图像过点P(－2，4)， 则该图像必经过点(　　) A．(2，4)　 B．(－2，－4)　 C．(－4，2)　 D．(4，－2)
函数y＝ax－2与y＝ax2(a≠0)在同一平面直角坐标系中的图像可能是(　　)
【中考·赤峰】函数y＝k(x－k)与y＝kx2，y＝(k≠0)在同一平面直角坐标系中的图像可能是(　　)
【中考·南宁】如图，垂直于x轴的直线AB分别与抛物线C1：y＝x2(x≥0)和抛物线C2：y＝ (x≥0)交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C 1交于点E，F，则 的值为(　　) B. C. D.
二次函数y＝ax2的性质
观察二次函数y=x2与 y =－x2的图象，你能发现什么问题？
在x轴的上方（除顶点外）
在x轴的下方（除顶点外）
当x=0时，最小值为0.
当x=0时，最大值为0.
当a>0时，在对称轴的左侧，y随着x的增大而减小。
当a>0时，在对称轴的右侧，y随着x的增大而增大。
当a<0时，在对称轴的左侧，y随着x的增大而增大。
当a<0时，在对称轴的右侧，y随着x的增大而减小。
例2 已知函数y＝－ x2，不画图象，回答下列各题． (1)开口方向：______； (2)对称轴：_____； (3)顶点坐标：______； (4)当x＞0时，y随x的增大而______； (5)当x____时，y＝0； (6)当x____时，函数值y最____，是___．
导引：根据二次函数y＝ax2(a≠0)的性质直接作答．
例3 已知抛物线y＝4x2过点(x1，y1)和点(x2，y2)，当x1＜x2＜0 时，y1 ________ y2.导引：方法一：不妨设x1＝－2，x2＝－1， 将它们分别代入y＝4x2中，得y1＝16， y2＝4，所以y1＞y2. 方法二：在平面直角坐标系中画出抛 物线y＝4x2，如图，显然y1＞y2. 方法三：因为a＝4＞0，x1＜x2＜0，在对称轴的左侧， y随x的增大而减小，所以y1＞y2.
方法一运用特殊值法，找出符合题目要求的x1和x2的 值，计算出对应的y1和y2的值，再比较它们的大小；方法二运用数形结合思想，根据题意画出图像，利用 图象来解题；方法三运用性质判断法，根据抛物线对应的函数表达 式的特点，结合图像的性质进行判断．
不画图像，请指出函数y＝－9x2图像的开口方向、对称轴、顶点坐 标以及最高(或最低)点．
开口向下，对称轴为y轴，顶点坐标为(0，0)，最高点为(0，0)．
先指出抛物线y＝－ x2的开口方向、对称轴和顶点坐标，然后再画出它的图像.
开口向下，对称轴为y轴，顶点坐标为(0，0)．图像如图．
3 下列关于函数y＝36x2的叙述中，错误的是(　　) A．图像的对称轴是y轴 B．图像的顶点是原点 C．当x＞0时，y随x的增大而增大 D．y有最大值4 (中考·玉林)抛物线y＝ x2，y＝x2，y＝－x2的共同性质是： ①都是开口向上；②都以点(0，0)为顶点；③都以y轴为对 称轴；④都关于x轴对称．其中正确的有(　　) A．1个 B．2个 C．3个 D．4个
5 【中考·连云港】已知抛物线y＝ax2(a＞0)过A (－2，y1)，B(1，y2)两点，则下列关系式一定 正确的是(　　) A．y1＞0＞y2 B．y2＞0＞y1 C．y1＞y2＞0 D．y2＞y1＞0
6 对于二次函数：①y＝3x2；②y＝ x2；③y＝ x2，它们的图像在同一坐标系中，开口大小的顺序用序号来表示应是(　　) A．②>③>① B．②>①>③ C．③>①>② D．③>②>①
7 若二次函数y＝－ax2，当x＝2时，y＝ ；则当x＝－2时，y＝________．
1. 画函数图像的步骤有哪些？2. 二次函数y=ax2的图像有哪些性质？
已知二次函数y＝x2，在－1≤x≤4这个范围内，求函数的最值．
易错点：不能准确地掌握二次函数y＝ax2的图像与性质
当x＝－1时，y＝(－1)2＝1；当x＝4时，y＝42＝16.∴在－1≤x≤4这个范围内，函数y＝x2的最小值是1，最大值是16.－1≤x≤4时，既包含了正数、零，又包含了负数，因此在这个范围内对应的函数值y随x的变化情况要分段研究．实际上，当x＝0时，函数取得最小值0.而x＝－1时，y＝1；x＝4时，y＝16，所以最大值为16.∵－1≤x≤4包含了x＝0，∴函数y＝x2的最小值为0.当x＝－1时，y＝1；当x＝4时，y＝16.∴当－1≤x≤4时，函数y＝x2的最大值为16.