






数学九年级下册30.2 二次函数的图像和性质图文ppt课件
展开二次函数y=ax2+c的图像 二次函数y=ax2+c的性质二次函数y=ax2+c的性质与y=ax2 之间的关系
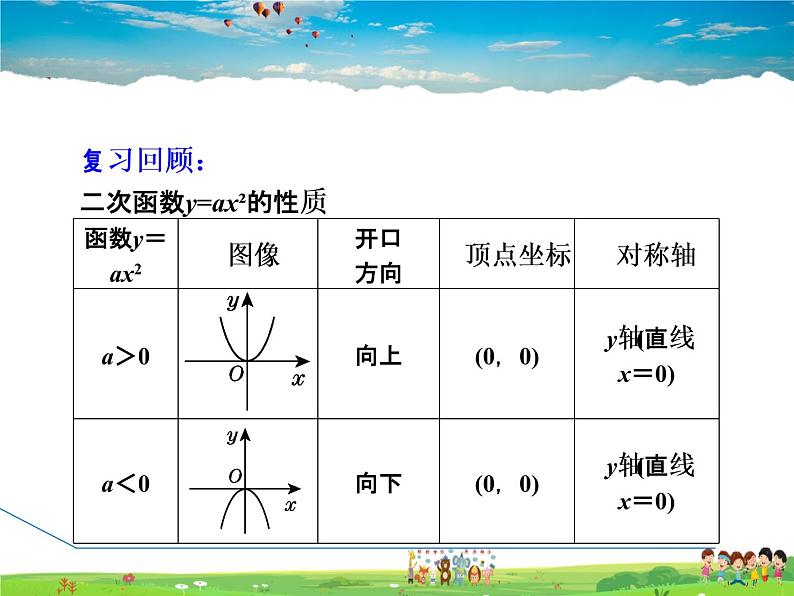
复习回顾:二次函数y=ax²的性质
二次函数y=ax2+c的图像
1.画二次函数y= x2+1的图像,你是怎样画的?与同伴进行 交流.2.二次函数y=x2+1的图像与二次函数y=x2 的图像有什么关 系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐 标分别是什么? 二次函数y = x2-1的图像呢?
在同一直角坐标系中,画出二次函数y=x2+1和y=x2 -1的图像
导引:根据二次函数y=ax2+c(a≠0)的图像的对称轴是 y轴直接选择.
函数y=ax2+c(a≠0)与函数y=ax2(a≠0)图像特征:只有顶点坐标不同,其他都相同.
1 抛物线y=ax2+(a-2)的顶点在x轴的下方,则a的取 值范围是____________.2 (中考·茂名)在平面直角坐标系中,下列函数的图像 经过原点的是( ) A.y= B.y=-2x-3 C.y=2x2+1 D.y=5x
3 在平面直角坐标系中,抛物线y=x2-1与x轴的交 点的个数是( ) A.3 B.2 C.1 D.0
在二次函数:①y=3x2 ; ②y= x2+1;③y=- x2-3中,图像开口大小顺序用序号表示为( )A.①>②>③ B.①>③>②C.②>③>① D.②>①>③
【中考·泰安】在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图像可能是( )
【中考·成都】二次函数y=2x2-3的图像是一条抛物线,下列关于该抛物线的说法,正确的是( )A.抛物线开口向下B.抛物线经过点(2,3)C.抛物线的对称轴是直线x=1D.抛物线与x轴有两个交点
二次函数y=ax2+c的性质
思考:(1)抛物线y=x2+1,y=x2-1的开口方向、对称轴、 顶点各是什么?(2)抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系?
抛物线y=x2+1: 开口向上, 对称轴是y轴, 顶点为(0,1).抛物线y=x2-1: 开口向上, 对称轴是y轴, 顶点为(0, -1).
二次函数y=ax2+c(a≠0)的图像和性质
例2 已知点(-7,y1),(3,y2),(-1,y3)都在抛物线y= ax2+k(a>0)上,则( ) A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3 ∵抛物线y=ax2+k(a>0)关于y轴对称,且点(3,y2) 在抛物线上,∴点(-3,y2)也在抛物线上. ∵(-7,y1),(-3,y2),(-1,y3)三点都在对称轴左 侧,在y轴左侧时,y随x的增大而减小,且-7<-3 <-1,∴y3<y2<y1.
对于在抛物线的对称轴两侧的函数值的大小比较,运用转化思想.先根据对称性将不在对称轴同侧的点转化为在对称轴同侧的点,再运用二次函数的增减性比较大小.
1 对于二次函数y=3x2+2,下列说法错误的是( ) A.最小值为2 B.图像与x轴没有公共点 C.当x<0时,y随x的增大而增大 D.图像的对称轴是y轴2 (中考·绍兴)已知点(x1,y1),(x2,y2)均在抛物线y= x2-1上,下列说法正确的是( ) A.若y1=y2,则x1=x2 B.若x1=-x2,则y1=-y2 C.若0
【2017·泸州】已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )A.3 B.4 C.5 D.6
二次函数y=ax2+c与y=ax2之间的关系
观察知1中抛物线y=x2+1,抛物线y=x2-1与抛物线y=x2,它们之间有什么关系?
抛物线y=x2+1,y=x2-1与抛物线y=x2的关系:
例3 〈广州〉将二次函数y=x2的图像向下平移1个单位, 则平移后的图像对应的二次函数的表达式为( ) A.y=x2-1 B.y=x2+1 C.y=(x-1)2 D.y=(x+1)2导引:由“上加下减”的原则可知,将二次函数y=x2的图 象向下平移1个单位,则平移后的图像对应的二 次函数的表达式为y=x2-1.
平移的方向决定是加还是减,平移的距离决定加或减的数值.
例4 抛物线y=ax2+c与抛物线y=-5x2的形状相同,开 口方向一样,且顶点坐标为(0,3),则其所对应的 函数表达式是什么?它是由抛物线y=-5x2怎样平 移得到的?导引:由两抛物线的形状、开口方向相同,可确定a的值; 再由顶点坐标为(0,3)可确定c的值,从而可确定 平移的方向和距离.
解:因为抛物线y=-5x2与抛物线y=ax2+c的形状相同, 开口方向一样,所以a=-5.又因为抛物线y=ax2+c 的顶点坐标为(0,3),所以c=3,其所对应的函数表 达式为y=-5x2+3,它是由抛物线y=-5x2向上平移 3个单位得到的.
根据二次函数y=ax2+c的图像和性质来解此类问题.a确定抛物线的形状及开口方向,c的正负和绝对值大小确定上下平移的方向和距离.
1 抛物线y=2x2+1是由抛物线y=2x2 ( )得到的. A.向上平移2个单位长度 B.向下平移2个单位长度 C.向上平移1个单位长度 D.向下平移1个单位长度2 (中考·上海)如果将抛物线y=x2+2向下平移1个单位长度,那么所得新抛物线的表达式是( ) A.y=(x-1)2+2 B.y=(x+1)2+2 C.y=x2+1 D.y=x2+3
当x<0时,y随着x的增大而减小.当x>0时,y随着x的增大而增大.
当x<0时,y随着x的增大而增大.当x>0时,y随着x的增大而减小.
二次函数y=ax2+c的图像与性质
x=0时,y最小= c
抛物线y=ax2 +c (a≠0)的图像可由y=ax2的图像通过上下平移|c|个单位得到.
能否通过上下平移二次函数y= x2的图像,使得到的新的函数图像过点(3,-3)?若能,说出平移的方向和距离;若不能,说明理由.
易错点:对平移的规律理解不透彻
能.设平移后的图像对应的二次函数表达式为y= x2+b, 将点(3,-3)的坐标代入表达式,得b=-6.所以平移的方向是向下,平移的距离是6个单位长度.
初中数学北师大版九年级下册1 二次函数试讲课ppt课件: 这是一份初中数学北师大版九年级下册1 二次函数试讲课ppt课件,共22页。PPT课件主要包含了复习导入,探究新知,yx2,①列表,②描点,③连线,抛物线,y2x2,与抛物线,有什么关系等内容,欢迎下载使用。
初中数学北师大版九年级下册1 二次函数一等奖ppt课件: 这是一份初中数学北师大版九年级下册1 二次函数一等奖ppt课件,共29页。PPT课件主要包含了学习目标,新课导入,y=ax2,上正下负,左加右减,新课讲解,提取二次项系数,化简去掉中括号,顶点坐标是,2列表等内容,欢迎下载使用。
冀教版九年级下册30.1 二次函数背景图课件ppt: 这是一份冀教版九年级下册30.1 二次函数背景图课件ppt,文件包含302第3课时二次函数yax2+bx+c的图像和性质ppt、302第3课时二次函数yax2+bx+c的图像和性质doc等2份课件配套教学资源,其中PPT共29页, 欢迎下载使用。













