2021-2022年11月 东直门中学 九年级期中试卷

北京市东直门中学2021-2022学年度第一学期期中考试

初三数学      2021.11

命题人：韩海丽       审稿人：彭忠

考试时间：120分钟     总分  100分

班级­­­­­___________      姓名____________       学号                     

第一部分（选择题）

一.选择题（每题2分，共16分）

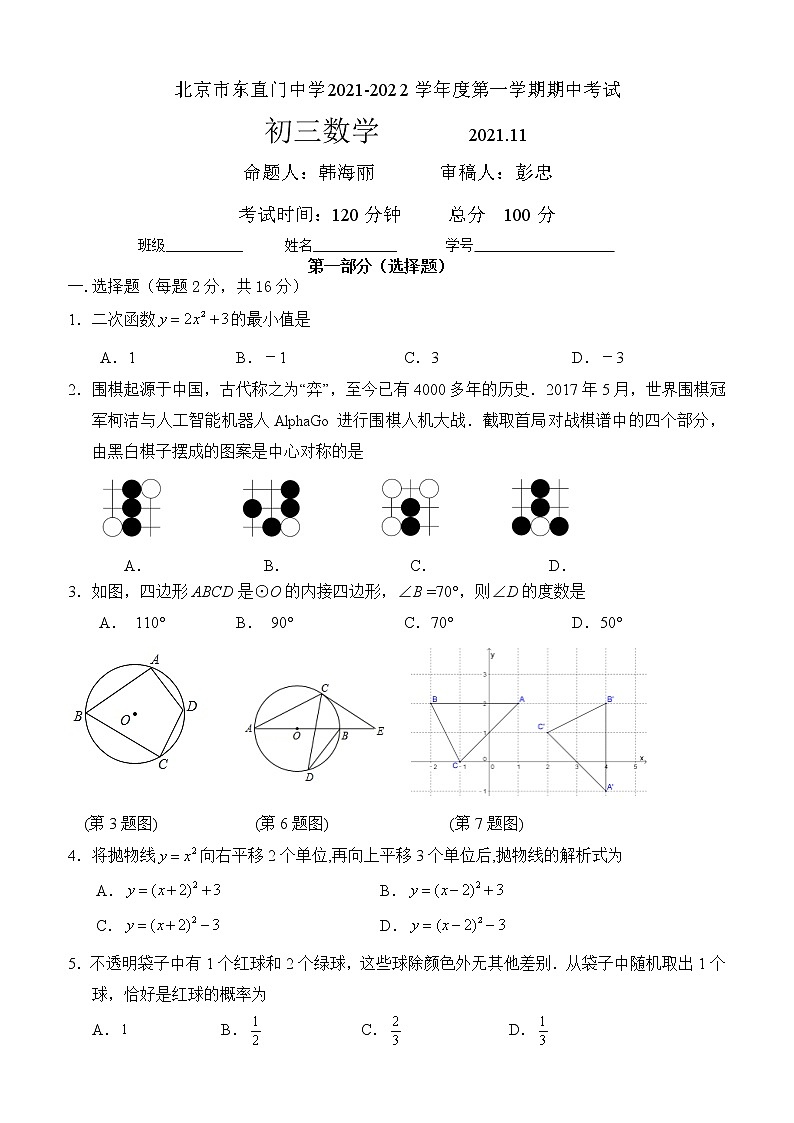
1．二次函数的最小值是                            

    A．1　 　        B．－1    　     C．3　         D．－3

2．围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是

       A．              B．               C．              D．

3．如图，四边形ABCD是⊙O的内接四边形，∠B =70°，则∠D的度数是　　

A． 110°         B． 90°         C．70°         D．50°

  (第3题图)            (第6题图)               (第7题图)                                                        

4．将抛物线向右平移2个单位,再向上平移3个单位后,抛物线的解析式为

  A．                B．   

C．        D．

5．不透明袋子中有1个红球和2个绿球，这些球除颜色外无其他差别．从袋子中随机取出1个球，恰好是红球的概率为

A． B． C．             D．

6．如图，AB是⊙O的直径，C．D是⊙O上的点，∠CDB=20°， 过点C作⊙O的切线交AB

的延长线于点E，则∠E等于

 A.40°                B． 50°                 C． 60°            D．70°

7．如图，在平面直角坐标系xOy中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，顺时针旋转90°得到△A’B’C’，则旋转中心的坐标是

     A．        B．        C．        D．

8．如图，点C是以点O为圆心，AB为直径的半圆上的动点（点C不与

点A，B重合），AB=4．设弦AC的长为x，△ABC的面积为y，则下列

图象中，能表示y与x的函数关系的图象大致是

        A.             B.                  C.                 D.

第二部分（非选择题）

二.填空题（每题2分，共16分）

9．点M（2，-4）、N关于原点对称，则点N的坐标是               .

10．请写出一个开口向下，且经过点（0，－1）的二次函数解析式：               .

11．如果一个圆锥的母线长为4，底面半径为1，那么这个圆锥的侧面积为     ．

12．已知正三角形ABC的边心距为cm，则正三角形的半径为　　　　　　cm．

13．关于x的一元二次方程有一个根是，则     ．

14．如图，抛物线与直线y＝bx＋c的两个交点坐标分别为，，则关于x的方程的解为__________．

     (第14题图)                             (第15题图)

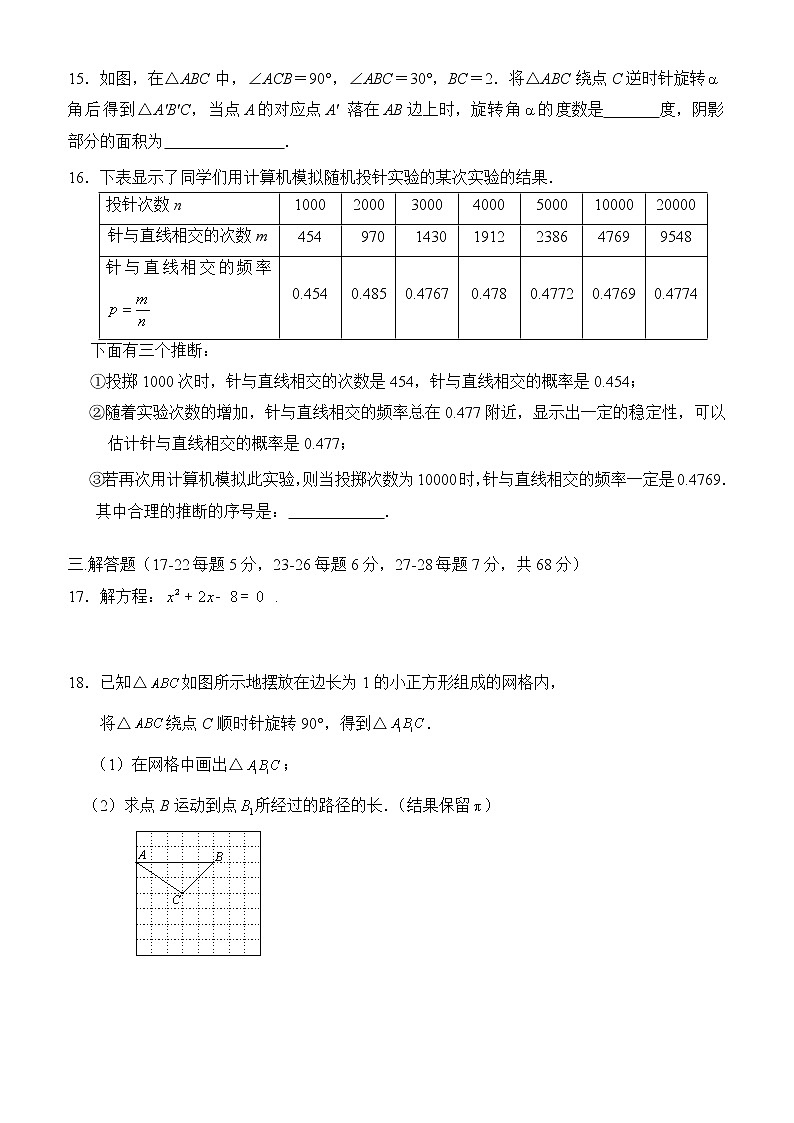
15．如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，BC＝2．将△ABC绕点C逆时针旋转角后得到△A′B′C，当点A的对应点A' 落在AB边上时，旋转角的度数是       度，阴影部分的面积为               ．

16．下表显示了同学们用计算机模拟随机投针实验的某次实验的结果．

下面有三个推断：

①投掷1000次时，针与直线相交的次数是454，针与直线相交的概率是0.454；

②随着实验次数的增加，针与直线相交的频率总在0.477附近，显示出一定的稳定性，可以估计针与直线相交的概率是0.477；

其中合理的推断的序号是：            ．

三.解答题（17-22每题5分，23-26每题6分，27-28每题7分，共68分）

17．解方程： .

18．已知△如图所示地摆放在边长为1的小正方形组成的网格内，

    将△绕点C顺时针旋转90°，得到△．

   （1）在网格中画出△；

（2）求点B运动到点所经过的路径的长．（结果保留）

19．如图1是博物馆展出的古代车轮实物，《周礼·考工记》记载：“……故兵车之轮六尺有六寸，田车之轮六尺有三寸……”据此， 我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．

     图1                图2

如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为r cm．

作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理的依据是：               ．

经测量，AB=90cm，CD=15cm，则AD=     cm；

用含r的代数式表示OD，OD=      cm．

在Rt△OAD中，由勾股定理可列出关于r的方程：

                 ，    

解得r=75．

通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．

20．四张大小、质地均相同的卡片上分别标有数字1，2，3，4，现将标有数字的一面朝下扣在桌子上，从中随机抽取一张，再从剩下的三张中随机抽取一张.

（1）用列表或画树状图的方法，列出前后两次抽得的卡片上所标数字的所有可能结果；

（2）求抽得的两张卡片上的数字之积为奇数的概率.

21．已知：关于x的方程有两个不相等的实数根. 

（1）求m的取值范围；     （2）写出一个满足条件的m的值，并求此时方程的根.

22．李明准备进行如下操作实验：把一根长40cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形．要使这两个正方形的面积和等于58cm2，则李明剪的这两个正方形的边长分别是多少？

    解决问题：设其中一个正方形的边长为x cm,则另一个正方形的边长可以表示为       

      请你帮助李明完成后面的解答过程.

23．抛物线上部分点的横坐标x，纵坐标y的对应值如下表：

     （1）根据上表填空： 

         ① 抛物线与x轴的交点坐标是          和          ；

         ② 抛物线经过点 (-3,      )；

         ③ 在对称轴右侧，y随x增大而        ；

      ( 2 )求该抛物线的解析式.

24．如图，Rt△ABC中，∠ACB=90°，点D在BC边上，以CD为直径的⊙O与

     直线AB相切于点E，且E是AB中点，连接OA．

（1）        求证：OA=OB；

（2）连接AD，若⊙O的半径为2，求AD．

25．某文具店销售一种进价为每本10元的笔记本，为获得高利润，以不低于进价进行销售，结果发现，每月销售量与销售单价之间的关系可以近似地看作一次函数：，物价部门规定这种笔记本每本的销售单价不得高于18元.

（1）当每月销售量为70本时，获得的利润为多少元？

（2）该文具店这种笔记本每月获得利润为元，求每月获得的利润元与销售单价之间的函数关系式，并写出自变量的取值范围；

（3）当销售单价定为多少元时，每月可获得最大利润，最大利润为多少元？

26．在平面直角坐标系xoy中，已知抛物线

（1）求抛物线的对称轴；

（2）当时，设抛物线与轴交于A，B两点（点A 在点B左侧），顶点为C，若△ABC 为等腰直角三角形，求a的值

（3）过T(0,t)（其中）且垂直轴的直线与抛物线交于M，N 两点. 若对于满足条件的任意t值，线段 MN 的长都不小于1，结合函数图象，求的取值范围

27．如图，已知是矩形的一条对角线，点在的延长线上，且.连接，与相交于点，与相交于点.

（1）依题意补全图形；

（2）若，解答下列问题：

① 判断与的位置关系，并说明理由；

② 连接,用等式表示线段，，之间的数量关系，并证明.

28．如图1，对于△PMN的顶点P及其对边MN上的一点Q，给出如下定义：以P为圆心，PQ为半径的圆与直线MN的公共点都在线段MN上，则称点Q为△PMN关于点P的内联点．

在平面直角坐标系xOy中：

（1）如图2，已知点，点B在直线上．  

① 若点，点，则在点O，C，A中，点_______是△AOB关于点B的内联点；

②若△AOB关于点B的内联点存在，求点B纵坐标n的取值范围；

（2）已知点，点，将点D绕原点O旋转得到点F，若△EOF关于点E的内联点存在，直接写出点F横坐标m的取值范围.

                    图1                         图2