初中数学北师大版七年级下册第五章 生活中的轴对称2 探索轴对称的性质教学设计

2　探索轴对称的性质

教学目标

一、基本目标

1．经历探索轴对称性质的过程，积累数学活动经验，发展空间观念．

2．理解轴对称的性质：在轴对称图形或两个成轴对称的图形中，对应点所连的线段被对称轴垂直平分，对应线段相等，对应角相等．

二、重难点目标

【教学重点】

探索并掌握轴对称的性质．

【教学难点】

运用轴对称的性质作图及利用轴对称的性质解决一些实际问题．

教学过程

环节1　自学提纲，生成问题

【5 min阅读】

阅读教材P118～P119的内容，完成下面练习．

【3 min反馈】

1．我们把沿对称轴折叠后能够重合的点叫做对应点，重合的线段叫做对应线段，重合的角叫做对应角.

2．轴对称的性质：在轴对称图形或两个成轴对称的图形中，对应点所连的线段被对称轴垂直平分，对应线段相等，对应角相等.

3．画轴对称图形，首先应确定对称轴，然后找出对称点.

4．如图，五边形ABCDE是轴对称图形，线段AF所在直线为对称轴，找出图中所有相等的线段和相等的角．

解：相等的线段：AB＝AE，CB＝DE，CF＝DF；相等的角：∠B＝∠E，∠C＝∠D，∠BAF＝∠EAF，∠AFD＝∠AFC．

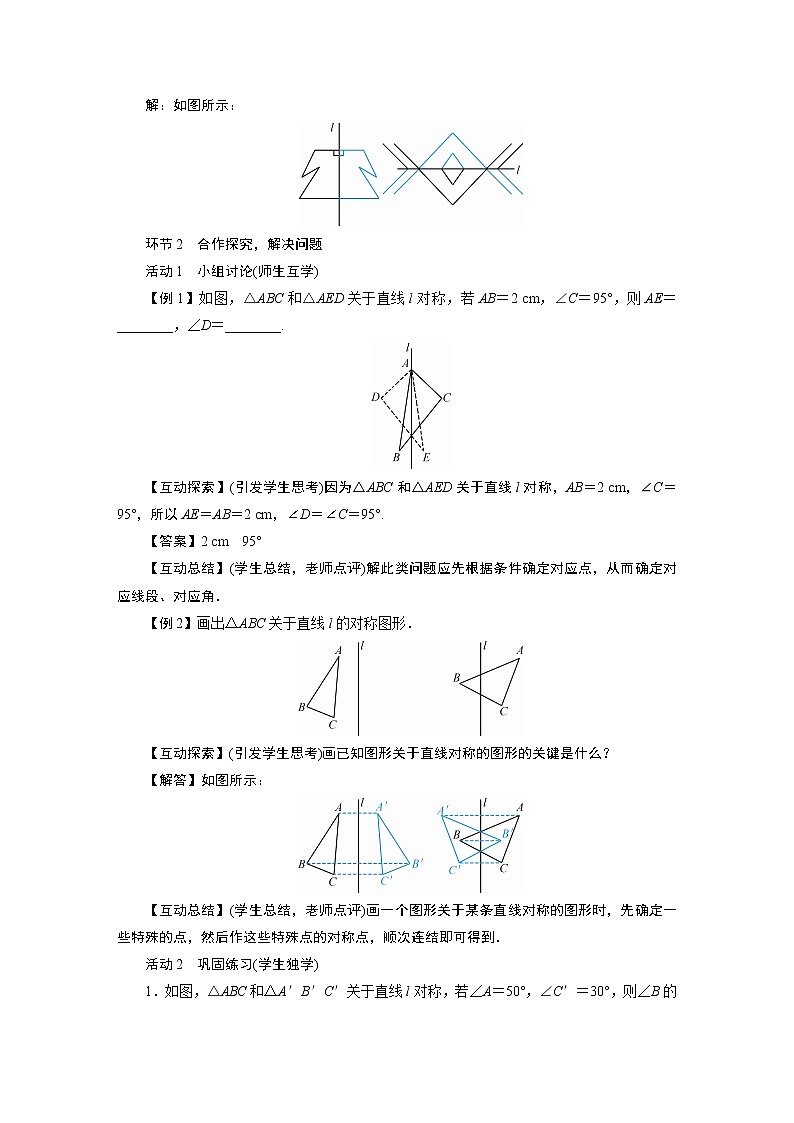
5．把如图所示的图形补成以直线l为对称轴的轴对称图形．

解：如图所示：

环节2　合作探究，解决问题

活动1　小组讨论(师生互学)

【例1】如图，△ABC和△AED关于直线l对称，若AB＝2 cm，∠C＝95°，则AE＝________，∠D＝________.

【互动探索】(引发学生思考)因为△ABC和△AED关于直线l对称，AB＝2 cm，∠C＝95°，所以AE＝AB＝2 cm，∠D＝∠C＝95°.

【答案】2 cm　95°

【互动总结】(学生总结，老师点评)解此类问题应先根据条件确定对应点，从而确定对应线段、对应角．

【例2】画出△ABC关于直线l的对称图形．

【互动探索】(引发学生思考)画已知图形关于直线对称的图形的关键是什么？

【解答】如图所示：

【互动总结】(学生总结，老师点评)画一个图形关于某条直线对称的图形时，先确定一些特殊的点，然后作这些特殊点的对称点，顺次连结即可得到．

活动2　巩固练习(学生独学)

1．如图，△ABC和△A′B′C′关于直线l对称，若∠A＝50°，∠C′＝30°，则∠B的度数为(　D　)

A．30°　 B．50°

C．90°　 D．100°

2．如图，直线MN是四边形AMBN的对称轴，与对角线交于点Q，点P是直线MN上面一点，下列判断错误的是(　D　)

A．AQ＝BQ　 B．AP＝BP

C．∠MAP＝∠MBP　 D．∠ANM＝∠NMB

3．如图，一种滑翔伞的形状是左右成轴对称的四边形ABCD，其中∠BAD＝150°，∠B＝40°，则∠BCD的度数是(　A　)

A．130°　 B．150°

C．40°　 D．65°

4．如图，将已知四边形分别在格点图中补成关于已知直线l、m、n、p为对称轴的轴对称的图形．

解：如图所示：

5．如图，在长方形的台球桌面上，选择适当的角度打击白球，可以使白球经过两次反弹后将黑球直接撞入袋中，此时∠1＝∠2，∠3＝∠4，并且∠2＋∠3＝90°，∠4＋∠5＝90°.如果黑球与洞口的连线和台球桌面边缘的夹角∠5＝30°，那么∠1应该等于多少度才能保证黑球准确入袋？请说明理由．

解：∠1＝30°才能保证黑球准确入袋．

理由如下：如图，因为∠5＝30°，

所以∠7＝∠5＝30°.

因为∠3＝∠4，

所以∠6＝∠7＝30°，

所以∠2＝∠6＝30°，

所以∠1＝∠2＝30°.

即∠1＝30°才能保证黑球准确入袋．

活动3　拓展延伸(学生对学)

【例3】如图，将长方形ABCD沿DE折叠，使点A落在BC上的点F处，若∠EFB＝60°，则∠CFD＝(　　)

A．20°　 B．30°

C．40°　 D．50°

【互动探索】根据图形翻折变换，得△ADE与△FDE关于直线DE成轴对称，所以△ADE≌△FDE，所以∠EFD＝∠EAD＝90°.因为∠EFB＝60°，所以∠CFD＝90°－∠EFB＝30°.

【答案】B

【互动总结】(学生总结，老师点评)折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，对应边和对应角相等．

环节3　课堂小结，当堂达标

(学生总结，老师点评)

练习设计

请完成本课时对应练习！