河南省信阳市罗山县2017-2018学年七年级（上）期末数学试卷（解析版）

这是一份河南省信阳市罗山县2017-2018学年七年级（上）期末数学试卷（解析版），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本题共8个小题，每小题3分，共24分，其中只有一个是正确的）
1．下列各数中，最大的数是（ ）
A．1B．﹣2C．|﹣3|D．0
2．如果□×，则“□”内应填的实数是（ ）
A．B．C．﹣D．﹣
3．实数a，b在数轴上的对应点如图所示，则下列不等式中错误的是（ ）
A．ab＞0B．a+b＜0C．＜1D．a﹣b＜0
4．如图，对于直线AB，线段CD，射线EF，其中能相交的图是（ ）
A．B．C．D．
5．方程2x=﹣4的解是（ ）
A．﹣1B．﹣2C．2D．﹣1
6．化简（x+1）﹣（1﹣x）+（x﹣1）的结果是（ ）
A．x﹣1B．3x+1C．3x﹣3D．3x﹣1
7．为减少雾霾天气，我们崇尚低碳生活，现有一个正方体的每个面都写有一个汉字，其平面展开图如图所示，则在该正方体中，和”崇“相对的面上写的汉字是（ ）
A．低B．碳C．生D．活
8．某时装标价为650元，某女士在”双十一“中以标价5折少30元的价钱购得，此时店主仍净赚50元，此时装进价为（ ）
A．275元B．295元C．245元D．325元

二、填空题（本大题共7小题，每小题3分，共18分）
9．如果水库的水位高于标准水位3米时，记作+3米，那么低于标准水位2米时，应记 米．
10．一个角的补角等于它的余角的6倍，则这个角的度数为 ．
11．据统计，国产动画片《大鱼海棠》票房收入约为566000000元，566000000用科学记数法表示为 ．
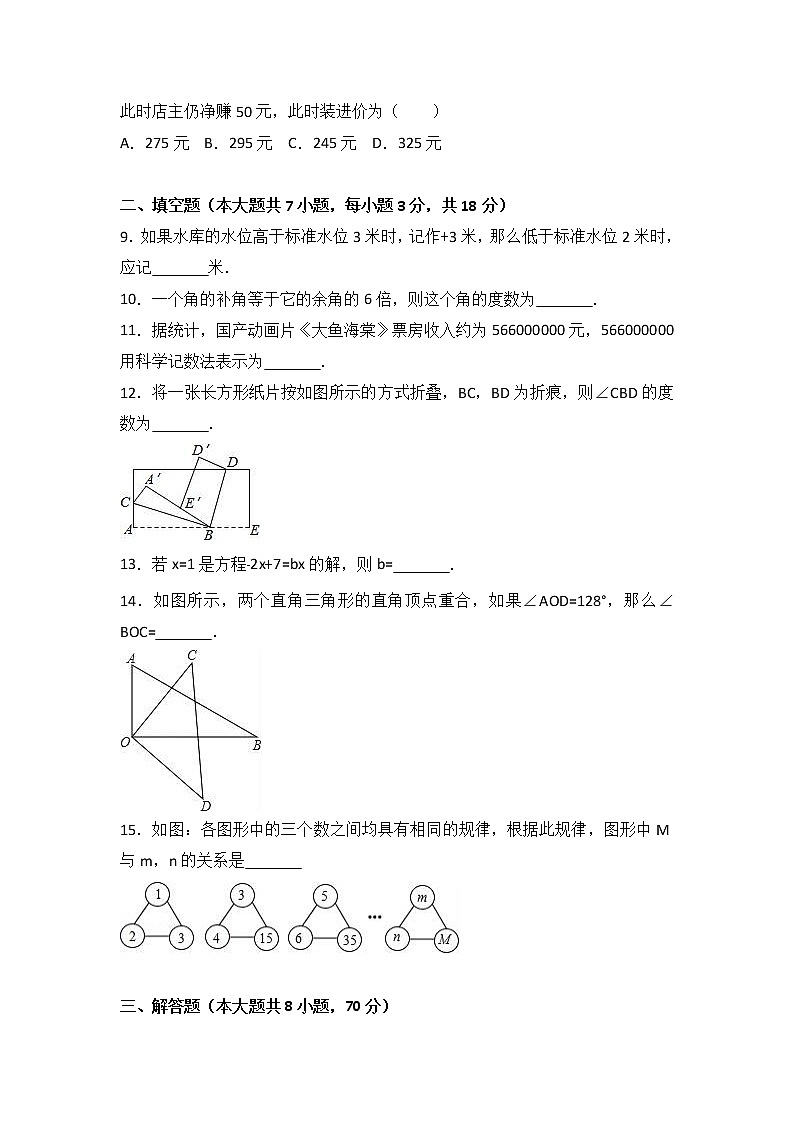
12．将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为 ．
13．若x=1是方程﹣2x+7=bx的解，则b= ．
14．如图所示，两个直角三角形的直角顶点重合，如果∠AOD=128°，那么∠BOC= ．
15．如图：各图形中的三个数之间均具有相同的规律，根据此规律，图形中M与m，n的关系是

三、解答题（本大题共8小题，70分）
16．计算：
（1）12﹣（﹣18）+（﹣7）﹣15
（2）13°53′×3﹣32°5′31″．
17．解方程：
（1）2x﹣（x+10）=6x；
（2）=3+．
18．先化简，再求值：x2+（2xy﹣3y2）﹣2（x2+yx﹣2y2），其中x=﹣1，y=2．
19．如图，已知直线AB和CD相交于O点，∠COE=90°，OF平分∠AOE，∠COF=28°，求∠BOD的度数．
20．如图，AD=，E是BC的中点，BE=，求线段AC和DE的长．
21．在”元旦“期间，罗山县尚文学校七一班的小明、小亮等同学随家长一同到信阳波尔登森林公园游玩，下面是购买门票时，小明与他爸爸的对话（如图），试根据图中的信息，解答下列问题：
（1）小明他们一共去了几个成人，几个学生？
（2）小明用所学的数字知识很快算出了哪种方式更省钱，你知道吗？请写出你的推算过程．
22．罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利=售价﹣进价）
（1）罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该购物中心第二次以第一次的进价又购进甲、乙两种商品．其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？
23．【背景知识】数轴上A点、B点表示的数为a、b，则A、B两点之间的距离AB=|a﹣b|；线段AB的中点M表示的数为．
【问题情境】已知数轴上有A、B两点，分别表示的数为﹣40和20，点A以每秒3个单位的速度沿数轴向右匀速运动，点B以每秒2个单位向左匀速运动．设运动时间为t秒（t＞0）．
（1）运动开始前，A、B两点的距离为 ；线段AB的中点M所表示的数为 ．
（2）它们按上述方式运动，A、B两点经过多少秒会相遇，相遇点所表示的数是什么？
（3）当t为多少时，线段AB的中点M表示的数为﹣5？并直接写出在这一运动过程中点M的运动方向和运动速度．

2017-2018学年河南省信阳市罗山县七年级（上）期末数学试卷
参考答案与试题解析

一、选择题（本题共8个小题，每小题3分，共24分，其中只有一个是正确的）
1．下列各数中，最大的数是（ ）
A．1B．﹣2C．|﹣3|D．0
【考点】18：有理数大小比较．
【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．
【解答】解：|﹣3|=3，
根据有理数比较大小的方法，可得
|﹣3|＞1＞0＞﹣2，
∴各数中，最大的数是|﹣3|．
故选：C．

2．如果□×，则“□”内应填的实数是（ ）
A．B．C．﹣D．﹣
【考点】1D：有理数的除法．
【分析】已知积与其中一个因数，求另一个因数，用除法．根据有理数的除法运算法则，得出结果．
【解答】解：1÷（﹣）=﹣．
故选D．

3．实数a，b在数轴上的对应点如图所示，则下列不等式中错误的是（ ）
A．ab＞0B．a+b＜0C．＜1D．a﹣b＜0
【考点】29：实数与数轴．
【分析】先根据数轴上点的特点确定a、b的符号和大小，再逐一进行判断即可求解．
【解答】解：由实数a，b在数轴上的对应点得：a＜b＜0，|a|＞|b|，
A、∵a＜b＜0，∴ab＞0，故选项正确；
B、∵a＜b＜0，∴a+b＜0，故选项正确；
C、∵a＜b＜0，∴＞1，故选项错误；
D、∵a＜b＜0，∴a﹣b＜0，故选项正确．
故选：C．

4．如图，对于直线AB，线段CD，射线EF，其中能相交的图是（ ）
A．B．C．D．
【考点】IA：直线、射线、线段．
【分析】根据直线、射线、线段的定义对各选项分析判断利用排除法求解．
【解答】解：A、直线AB与线段CD不能相交，故本选项错误；
B、直线AB与射线EF能够相交，故本选项正确；
C、射线EF与线段CD不能相交，故本选项错误；
D、直线AB与射线EF不能相交，故本选项错误．
故选B．

5．方程2x=﹣4的解是（ ）
A．﹣1B．﹣2C．2D．﹣1
【考点】86：解一元一次方程．
【分析】方程两边除以2将x系数化为1，即可求出解．
【解答】解：方程2x=﹣4，
解得：x=﹣2，
故选B

6．化简（x+1）﹣（1﹣x）+（x﹣1）的结果是（ ）
A．x﹣1B．3x+1C．3x﹣3D．3x﹣1
【考点】44：整式的加减．
【分析】原式去括号合并即可得到结果．
【解答】解：原式=x+1﹣1+x+x﹣1=3x﹣1，
故选D

7．为减少雾霾天气，我们崇尚低碳生活，现有一个正方体的每个面都写有一个汉字，其平面展开图如图所示，则在该正方体中，和”崇“相对的面上写的汉字是（ ）
A．低B．碳C．生D．活
【考点】I8：专题：正方体相对两个面上的文字．
【分析】利用正方体及其表面展开图的特点解题．
【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“崇”与面“低”相对，面“尚”与面“碳”相对，面“生”与面“活”相对．
故选A．

8．某时装标价为650元，某女士在”双十一“中以标价5折少30元的价钱购得，此时店主仍净赚50元，此时装进价为（ ）
A．275元B．295元C．245元D．325元
【考点】8A：一元一次方程的应用．
【分析】设此时装进价为x元，根据，现售价﹣进价=利润，即可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：设此时装进价为x元，
根据题意得：650×0.5﹣30﹣x=50，
解得：x=245．
故选C．

二、填空题（本大题共7小题，每小题3分，共18分）
9．如果水库的水位高于标准水位3米时，记作+3米，那么低于标准水位2米时，应记 ﹣2 米．
【考点】11：正数和负数．
【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
【解答】解：“高”和“低”相对，若水库的水位高于标准水位3米时，记作+3米，则低于标准水位2米时，应记﹣2米．

10．一个角的补角等于它的余角的6倍，则这个角的度数为 72° ．
【考点】IL：余角和补角．
【分析】利用题中的关系“一个角的补角等于这个角的余角的6倍”作为相等关系列方程求解即可．
【解答】解：设这个角为x，则它的补角为
余角为（90°﹣x），由题意得：
180°﹣x=6（90°﹣x），
180°﹣x=540°﹣6x，
6x﹣x=540°﹣180°，
5x=360°，
x=72°．
答：这个角的度数为72°．
故答案为：72°．

11．据统计，国产动画片《大鱼海棠》票房收入约为566000000元，566000000用科学记数法表示为 5.66×108 ．
【考点】1I：科学记数法—表示较大的数．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：566000000=5.66×108．
故答案为：5.66×108．

12．将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为 90° ．
【考点】IK：角的计算；PB：翻折变换（折叠问题）．
【分析】根据折叠的性质得到∠ABC=∠A′BC，∠EBD=∠E′BD，再根据平角的定义有∠ABC+∠A′BC+∠EBD+∠E′BD=180°，易得A′BC+∠E′BD=180°×=90°，则∠CBD=90°．
【解答】解：∵一张长方形纸片沿BC、BD折叠，
∴∠ABC=∠A′BC，∠EBD=∠E′BD，
而∠ABC+∠A′BC+∠EBD+∠E′BD=180°，
∴∠A′BC+∠E′BD=180°×=90°，
即∠CBD=90°．
故答案为：90°．

13．若x=1是方程﹣2x+7=bx的解，则b= 5 ．
【考点】85：一元一次方程的解．
【分析】根据方程的解满足方程，可得关于b的方程，根据解方程，可得答案．
【解答】解：由x=1是方程﹣2x+7=bx的解，得
﹣2+7=b，
∴b=5，
故答案为：5．

14．如图所示，两个直角三角形的直角顶点重合，如果∠AOD=128°，那么∠BOC= 52° ．
【考点】IL：余角和补角．
【分析】根据题意得到∠AOB=∠COD=90°，再计算∠BOD=∠AOD﹣90°=38°，然后根据∠BOC=∠COD﹣∠BOD进行计算即可．
【解答】解：∵∠AOB=∠COD=90°，
而∠AOD=128°，
∴∠BOD=∠AOD﹣90°=38°，
∴∠BOC=∠COD﹣∠BOD=90°﹣38°=52°．
故答案为52°．

15．如图：各图形中的三个数之间均具有相同的规律，根据此规律，图形中M与m，n的关系是 M=m×（n+1）
【考点】37：规律型：数字的变化类．
【分析】根据m、n所在位置，求出出两个数列，按照每个数列的序号找出一般式即可．
【解答】解：m、n所在位置表示的数如下：
第1个图形：m=1，n=2，M=3=1×（2+1），
第2个图形：m=3，n=4，M=15=3×（4+1），
第3个图形：m=5，n=6，M=35=5×（6+1），
…
在第m或n个图形中：
M=m×（n+1）．
故答案为：M=m×（n+1）．

三、解答题（本大题共8小题，70分）
16．计算：
（1）12﹣（﹣18）+（﹣7）﹣15
（2）13°53′×3﹣32°5′31″．
【考点】II：度分秒的换算；1B：有理数的加减混合运算．
【分析】（1）根据有理数的加减法，可得答案；
（2）根据度分秒的换算，可得答案．
【解答】（1）原式=12+18﹣7﹣15=30﹣7﹣15=8；
（2）13°53′×3﹣32°5′31″
=41°39′﹣32°5′31″
=9°33′29″．

17．解方程：
（1）2x﹣（x+10）=6x；
（2）=3+．
【考点】86：解一元一次方程．
【分析】（1）方程去括号，移项合并，把x系数化为1，即可求出解；
（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
【解答】解：（1）方程去括号得：2x﹣x﹣10=6x，
移项合并得：5x=﹣10，
解得：x=﹣2；
（2）方程去分母得：2（x+1）=12+2﹣x，
去括号得：2x+2=12+2﹣x，
移项合并得：3x=12，
解得：x=4．

18．先化简，再求值：x2+（2xy﹣3y2）﹣2（x2+yx﹣2y2），其中x=﹣1，y=2．
【考点】45：整式的加减—化简求值．
【分析】先根据去括号、合并同类项化简，然后再把x、y的值代入求解；
【解答】解：x2+（2xy﹣3y2）﹣2（x2+yx﹣2y2），
=x2+2xy﹣3y2﹣2x2﹣2yx+4y2，
=﹣x2+y2，
当x=﹣1，y=2时，
原式=﹣（﹣1）2+22=﹣1+4=3．

19．如图，已知直线AB和CD相交于O点，∠COE=90°，OF平分∠AOE，∠COF=28°，求∠BOD的度数．
【考点】J2：对顶角、邻补角；IJ：角平分线的定义．
【分析】根据角的和差，可得∠EOF的度数，根据角平分线的性质，可得∠AOC的度数，根据补角的性质，可得答案．
【解答】解：由角的和差，得∠EOF=∠COE﹣COF=90°﹣28°=62°．
由角平分线的性质，得∠AOF=∠EOF=62°．
由角的和差，得∠AOC=∠AOF﹣∠COF=62°﹣28°=34°．
由对顶角相等，得
∠BOD=∠AOC=34°．

20．如图，AD=，E是BC的中点，BE=，求线段AC和DE的长．
【考点】ID：两点间的距离．
【分析】根据线段中点的性质，可得BC的长，根据线段的和差，可得AC的长，可得关于DB的方程，根据解方程，可得DB的长，再根据线段的和差，可得答案．
【解答】解：由E是BC的中点，BE=，得
BC=2BE=2×2=4cm，
AB=3×2=6cm，
由线段的和差，得
AC=AB+BC=4+6=10cm；
AB=AD+DB，
即DB+DB=6，
解得DB=4cm．
由线段的和差，得
DE=DB+BE=4+2=6cm．

21．在”元旦“期间，罗山县尚文学校七一班的小明、小亮等同学随家长一同到信阳波尔登森林公园游玩，下面是购买门票时，小明与他爸爸的对话（如图），试根据图中的信息，解答下列问题：
（1）小明他们一共去了几个成人，几个学生？
（2）小明用所学的数字知识很快算出了哪种方式更省钱，你知道吗？请写出你的推算过程．
【考点】8A：一元一次方程的应用．
【分析】（1）设去了x个成人，则去了（15﹣x）个学生，根据爸爸说的话，可确定相等关系为：成人的票价+学生的票价=750元，据此列方程求解；
（2）计算团体票所需费用，和750元比较即可求解．
【解答】解：（1）设成人人数为x人，则学生人数为（15﹣x）人，
则 60x+60/2（15﹣x）=750，
解得：x=10，
答：学生人数为15﹣10=5人，成人人数为10人；
（2）如果买团体票，按16人计算，共需费用：
60×0.6×16=576（元），
因为576＜750，所以，购团体票更省钱．

22．罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利=售价﹣进价）
（1）罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该购物中心第二次以第一次的进价又购进甲、乙两种商品．其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？
【考点】8A：一元一次方程的应用．
【分析】（1）设第一次购进甲种商品x件，则乙的件数为（x+15）件，根据总进价=甲种商品单件进价×数量+乙种商品单件进价×数量即可得出关于x的一元一次方程，解之即可得出x的值，再根据总利润=甲种商品单件利润×数量+乙种商品单件利润×数量代入数据即可得出结论；
（2）设第二次乙种商品是按原价打y折销售，根据总利润=甲种商品单件利润×数量+乙种商品单件利润×数量即可得出关于y的一元一次方程，解之即可得出结论．
【解答】解：（1）设第一次购进甲种商品x件，则乙的件数为（x+15）件，
根据题意得：20x+30（x+15）=5000，
解得：x=130，
∴x+15=65+15=80，
（29﹣20）×130+（40﹣30）×80=1970（元）．
答：两种商品全部卖完后可获得1970元利润．
（2）设第二次乙种商品是按原价打y折销售，
根据题意得：（29﹣20）×130+（40×﹣30）×80×3=1970+160，
解得：y=8.5．
答：第二次乙种商品是按原价打8.5折销售．

23．【背景知识】数轴上A点、B点表示的数为a、b，则A、B两点之间的距离AB=|a﹣b|；线段AB的中点M表示的数为．
【问题情境】已知数轴上有A、B两点，分别表示的数为﹣40和20，点A以每秒3个单位的速度沿数轴向右匀速运动，点B以每秒2个单位向左匀速运动．设运动时间为t秒（t＞0）．
（1）运动开始前，A、B两点的距离为 60 ；线段AB的中点M所表示的数为 ﹣10 ．
（2）它们按上述方式运动，A、B两点经过多少秒会相遇，相遇点所表示的数是什么？
（3）当t为多少时，线段AB的中点M表示的数为﹣5？并直接写出在这一运动过程中点M的运动方向和运动速度．
【考点】8A：一元一次方程的应用；13：数轴．
【分析】（1）根据A、B两点之间的距离AB=|a﹣b|，线段AB的中点M表示的数为代入可得；
（2）根据相遇后，A、B两点所表示的数相同，列方程可求解，再代回可知相遇点表示的数；
（3）根据线段AB的中点表示的数为﹣5列出方程，解得，将中点M的两个时刻所表示的数比较可知运动方向和速度．
【解答】解：（1）根据题意可知，运动开始前，A、B两点的距离AB=|﹣40﹣20|=60；
线段AB的中点M所表示的数为：；
（2）设它们按上述方式运动，A、B两点经过x秒会相遇，则
点A运动x秒后所在位置的点表示的数为﹣40+3x；点B运动x秒后所在位置的点表示的数为20﹣2x；
根据题意，得：﹣40+3x=20﹣2x
解得 x=12，
∴它们按上述方式运动，A、B两点经过12秒会相遇，
相遇点所表示的数是：﹣40+3x=﹣40+3×12=﹣4；
答：A、B两点经过12秒会相遇，相遇点所表示的数是﹣4．
（3）根据题意，得：，
解得 t=10，
∵t=0时，中点M表示的数为﹣10；t=10时，中点M表示的数为﹣5；
∴中点M的运动方向向右，运动速度为．
答：经过10秒，线段AB的中点M表示的数是﹣5．M点的运动方向向右，运动速度为每秒个单位长度．
故答案为：（1）60，﹣10．

2017年6月15日
甲
乙
进价（元/件）
20
30
售价（元/件）
29
40

甲
乙
进价（元/件）
20
30
售价（元/件）
29
40