广东省九年级上册人教版数学期末考试同步冲刺本练习题

这是一份广东省九年级上册人教版数学期末考试同步冲刺本练习题，共17页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。


1. 如果关于x的方程x2−mx+6=0有一根是−3，那么这个方程的另一个根是（ ）
A.−5B.5C.−2D.2

2. 抛物线y=x2+2x+3的对称轴是( )
A.直线x=1B.直线x=−1C.直线x=−2D.直线x=2

3. 如图，把一个直角三角板△ACB绕着30∘角的顶点B顺时针旋转，使得点A与CB的延长线上的点E重合，连接CD，则∠BDC的度数为（ ）

A.15∘B.20∘C.25∘D.30∘

4. 为了解圭峰会城九年级女生身高情况，随机抽取了圭峰会城九年级100名女生，她们的身高x(cm)统计如下：
根据以上结果，随机抽查圭峰会城九年级1名女生，身高不低于155cm的概率是（ ）

5. 如图，A、D是⊙O上的两个点，BC是直径，若∠D=35∘，则∠OAC的度数是（）

A.35∘B.55∘C.65∘D.70∘

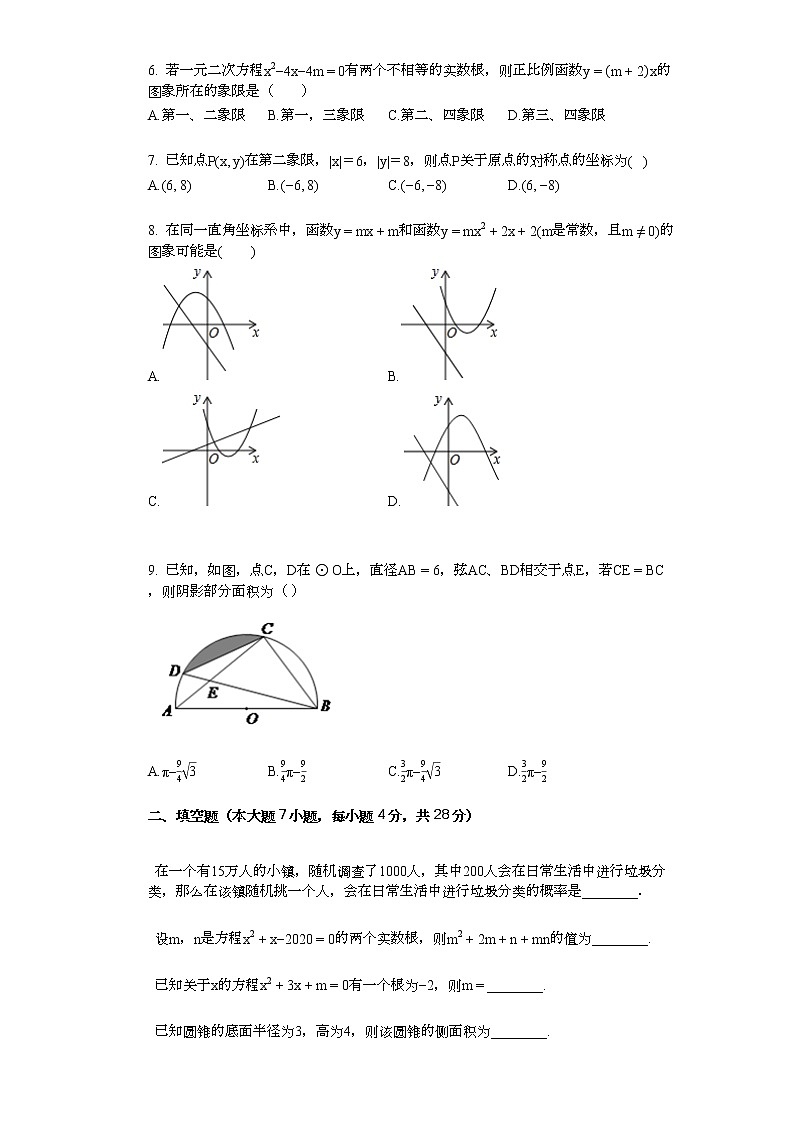
6. 若一元二次方程x2−4x−4m=0有两个不相等的实数根，则正比例函数y=m+2x的图象所在的象限是（ ）
A.第一、二象限B.第一，三象限C.第二、四象限D.第三、四象限

7. 已知点P(x, y)在第二象限，|x|＝6，|y|＝8，则点P关于原点的对称点的坐标为( )
A.(6, 8)B.(−6, 8)C.(−6, −8)D.(6, −8)

8. 在同一直角坐标系中，函数y=mx+m和函数y=mx2+2x+2(m是常数，且m≠0)的图象可能是( )
A.B.
C.D.

9. 已知，如图，点C，D在⊙O上，直径AB=6，弦AC、BD相交于点E，若CE=BC，则阴影部分面积为（ ）

A.π−943B.94π−92C.32π−943D.32π−92
二、填空题（本大题7小题，每小题4分，共28分）

在一个有15万人的小镇，随机调查了1000人，其中200人会在日常生活中进行垃圾分类，那么在该镇随机挑一个人，会在日常生活中进行垃圾分类的概率是________．

设m，n是方程x2+x−2020=0的两个实数根，则m2+2m+n+mn的值为________.

已知关于x的方程x2+3x+m=0有一个根为−2，则m=________.

已知圆锥的底面半径为3，高为4，则该圆锥的侧面积为________.

如图，抛物线y=−x2+2x+与x轴交于A，B两点，则点B的坐标是________


如图，把△ABC绕点C按顺时针方向旋转35∘，得到△A′B′C，A′B′交AC于点D．若∠A′DC=90∘，则 ∠A=________.


如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30∘，CD=23，则阴影部分的面积为________．

三、解答题（一）（本大题3小题，每小题6分，共18分）

解方程：5x(x+1)＝2(x+1)

如图，在正方形网格中，每个小正方形的边长均为1个单位．
（1）△ABC绕着点C顺时针旋转90∘，画出旋转后对应的△A1B1C1；

（2）求△ABC旋转到△A1B1C时，BB1的长．

如图，甲分为三等分数字转盘，乙为四等分数字转盘，自由转动转盘．
(1)转动甲转盘，指针指向的数字小于3的概率是________.

(2)同时自由转动两个转盘，用列表或画树状图的方法求两个转盘指针指向的数字均为奇数的概率．

某钢铁厂计划今年第一季度一月份的总产量为500t，三月份的总产量为720t，若平均每月的增长率相同．
(1)求第一季度平均每月的增长率；

(2)如果第二季度平均每月的增长率保持与第一季度平均每月的增长率相同，请你估计该厂今年5月份总产量能否突破1000t？

已知二次函数y=x2−2mx+2m2+1（m是常数）．
（1）求证：不论m为何值，该函数的图象与x轴没有公共点；

（2）如果把该函数图象沿y轴向下平移5个单位后，得到的函数图象与x轴只有一个公共点，求m的值？

如图，在Rt△ABC中，AB＝AC，D、E是斜边BC上的两点，∠EAD＝45∘，将△ADC绕点A顺时针旋转90∘，得到△AFB，连接EF．

（1）求证：EF＝ED；

（2）若AB＝22，CD＝1，求FE的长．

如图，已知AB是⊙O的直径，点C在⊙O上，点P是AB延长线上一点，∠BCP＝∠A．

（1）求证：直线PC是⊙O的切线；

（2）若CA＝CP，⊙O的半径为2，求CP的长．

如图，二次函数y＝x2+bx+c的图象与x轴相交于点A、B两点，与y轴相交于点C(0, −3)，抛物线的对称轴为直线x＝1．

（1）求此二次函数的解析式；

（2）若抛物线的顶点为D，点E在抛物线上，且与点C关于抛物线的对称轴对称，直线AE交对称轴于点F，试判断四边形CDEF的形状，并证明你的结论．
参考答案与试题解析
广东省九年级上册人教版数学期末考试同步冲刺本
一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的.
1.
【答案】
C
【考点】
根与系数的关系
解一元二次方程-因式分解法
一元二次方程的解
【解析】
此题暂无解析
【解答】
C
2.
【答案】
B
【考点】
二次函数的性质
【解析】
先把一般式化为顶点式，然后根据二次函数的性质确定抛物线的对称轴方程．
【解答】
解：∵ y=x2+2x+3=(x+1)2+2，
∴ 抛物线的对称轴为直线x=−1．
故选B.
3.
【答案】
A
【考点】
旋转的性质
【解析】
根据图形旋转的性质得出△ABC≅△EBD，可得出BC＝BD，根据图形旋转的性质求出∠EBD的度数，再由等腰三角形的性质即可得出∠BDC的度数．
【解答】
∵ △EBD由△ABC旋转而成，
∴ △ABC≅△EBD，
∴ BC＝BD，∠EBD＝∠ABC＝30∘，
∴ ∠BDC＝∠BCD，∠DBC＝180−30∘＝150∘，
∴ ∠BDC=12(180∘−150∘)＝15∘；
4.
【答案】
D
【考点】
频数（率）分布表
概率公式
【解析】
直接利用不低于155cm的频数除以总数得出答案．
【解答】
∵ 身高不低于155cm的有52+18+5＝75（人），
∴ 随机抽查圭峰会城九年级1名女生，身高不低于155cm的概率是：75100=0.75．
5.
【答案】
B
【考点】
圆周角定理
【解析】
解：D=35∘
∴AOC=2∠D=70∘
∠OAC=180∘−∠AOC+2=110∘+2=55∘故选B．
【解答】
B
6.
【答案】
B
【考点】
一次函数的性质
一次函数的图象
解一元二次方程-公式法
【解析】
此题暂无解析
【解答】
B
7.
【答案】
D
【考点】
关于原点对称的点的坐标
关于x轴、y轴对称的点的坐标
绝对值
【解析】
根据P在第二象限可以确定x，y的符号，再根据|x|=6,|y|=8就可以得到x，y的值，得出P点的坐标，进而求出点P关于原点的对称
点的坐标．
【解答】
∵|x|=6,|y|=8
x=±6,y=±8
点P在第二象限，
x<0,y>0
x=−6,y=8
即点P的坐标是−6,8，关于原点的对称点的坐标是6,−8
故选：D．
8.
【答案】
D
【考点】
二次函数的图象
【解析】
关键是m的正负的确定，对于二次函数y=ax2+bx+c，当a>0时，开口向上；当a<0时，开口向下．对称轴为x=−b2a，与y轴的交点坐标为(0, c)．
【解答】
解：A．由函数y=mx+m的图象可知m<0，
即函数y=mx2+2x+2开口方向朝下，
对称轴为x=−b2a=−22m=−1m>0，
则对称轴应在y轴右侧，与图象不符，
故A选项错误；
B．由函数y=mx+m的图象可知m<0，
即函数y=mx2+2x+2开口方向朝下，
开口方向朝下，与图象不符，故B选项错误；
C．由函数y=mx+m的图象可知m>0，
即函数y=mx2+2x+2开口方向朝上，
对称轴为x=−b2a=−22m=−1m<0，
则对称轴应在y轴左侧，与图象不符，故C选项错误；
D．由函数y=mx+m的图象可知m<0，
即函数y=mx2+2x+2开口方向朝下，
对称轴为x=−b2a=−22m=−1m>0，
则对称轴应在y轴右侧，与图象相符，故D选项正确．
故选D．
9.
【答案】
B
【考点】
扇形面积的计算
等边三角形的性质与判定
【解析】
连接OD、OC，由题意可得，阴影部分面积=扇形OCD的面积-三角形OCD的面积，结合题意易证得三角形OCD是等边三角形，于是阴影部分面积可求解．
【解答】
B
二、填空题（本大题7小题，每小题4分，共28分）
【答案】
15
【考点】
概率公式
【解析】
用所抽样本中会进行垃圾分类的人数除以抽取的总人数即可得．
【解答】
在该镇随机挑一个人，会在日常生活中进行垃圾分类的概率是2001000=15，
【答案】
−1
【考点】
根与系数的关系
【解析】
此题暂无解析
【解答】
−1
【答案】
2
【考点】
一元二次方程根的分布
【解析】
此题暂无解析
【解答】
2
【答案】
15π
【考点】
柱体、锥体、台体的侧面积和表面积
【解析】
此题暂无解析
【解答】
15π
【答案】
(−1, 0)
【考点】
抛物线与x轴的交点
【解析】
此题暂无解析
【解答】
(−1, 0)
【答案】
55∘
【考点】
三角形内角和定理
旋转的性质
【解析】
此题暂无解析
【解答】
解：∵ 把△ABC 绕点C顺时针旋转35∘后得到△A′B′C,
∴ ∠A′CA=35∘，
而∠A′DC=90∘，
∴ ∠A=∠A′=90∘−35∘=55∘.
故答案为：55∘.
【答案】
2π3
【考点】
垂径定理
扇形面积的计算
【解析】
根据垂径定理求出CE=DE的值，得到S△OCE=S△ODE ，根据圆周角定理得到∠COB=2∠CDB，根据扇形面积公式求出S加加OBD的值．
【解答】
2π3
三、解答题（一）（本大题3小题，每小题6分，共18分）
【答案】
解：5x(x+1)−2(x+1)=0
x+15x−2=0
则x+1=0或5x−2=0
解得x=−1或x=25
【考点】
解一元二次方程-因式分解法
【解析】
先移项，再利用因式分解法求解可得．
【解答】
解：5x(x+1)−2(x+1)=0
x+15x−2=0
则x+1=0或5x−2=0
解得x=−1或x=25
【答案】
（1）如图所示，ΔA1B1C1即为所求；
（2）BB1的长为：90×π×3180=32π
【考点】
作图-旋转变换
旋转的性质
弧长的计算
【解析】
（1）依据△ABC绕着点C顺时针旋转90∘，即可画出旋转后对应的ΔA1B1C1
（2）依据弧长计算公式，即可得到弧BB1的长．
【解答】
（1）如图所示，ΔA1B1C1即为所求；
（2）BB1的长为：90×π×3180=32π
【答案】
23
（2）根据题意，画树状图如下：
由树状图知，共有12种等可能情况，其中两个转盘指针指向的数字均为奇数的有4种情况，P（两个转盘指针指向的数字均为奇数）=412=13
【考点】
列表法与树状图法
【解析】
此题暂无解析
【解答】
解：（1）甲转盘共有1，2，3三个数字，其中小于3的有1，2，
∴ P（转动甲转盘，指针指向的数字小于3）=23
故答案为23
（2）根据题意，画树状图如下：
由树状图知，共有12种等可能情况，其中两个转盘指针指向的数字均为奇数的有4种情况，P（两个转盘指针指向的数字均为奇数）=412=13
【答案】
解：(1)设第一季度平均每月的增长率为x，
根据题意得：500(1+x)2=720，
解得：x1=0.2=20%，x2=−2.2(舍去)．
答：第一季度平均每月的增长率为20%．
(2)∵ 3月份的总产量为720t，且平均每月的增长率为20%，
∴ 5月份的总产量为720×(1+20%)2=1036.8(t)．
∵ 1036.8>1000，
∴ 该厂今年5月份总产量能突破1000t．
【考点】
一元二次方程的应用——增长率问题
【解析】


【解答】
解：(1)设第一季度平均每月的增长率为x，
根据题意得：500(1+x)2=720，
解得：x1=0.2=20%，x2=−2.2(舍去)．
答：第一季度平均每月的增长率为20%．
(2)∵ 3月份的总产量为720t，且平均每月的增长率为20%，
∴ 5月份的总产量为720×(1+20%)2=1036.8(t)．
∵ 1036.8>1000，
∴ 该厂今年5月份总产量能突破1000t．
【答案】
（1）∵Δ=4m2−42m2+1
=−4m2−4<0
∴ 不论m为何值，该函数的图象与x轴没有公共点；
（2）∵y=x2−2mx+2m2+1=x−m2+m2+1
∴ 抛物线的顶点坐标为m,m2+1
∵ 把该函数图象沿y轴向下平移5个单位后，得到的函数图象与x轴只有一个公共点，
∴ m2+1=5
解得m1=2,m2=−2
即m的值为±2
【考点】
根的判别式
二次函数图象的平移规律
【解析】
（1）根据题意证明Δ<0即可求解；
（2）先把函数化为顶点式，再根据平移后的图像特点进行求解．
【解答】
（1）∵Δ=4m2−42m2+1
=−4m2−4<0
∴ 不论m为何值，该函数的图象与x轴没有公共点；
（2）∵y=x2−2mx+2m2+1=x−m2+m2+1
∴ 抛物线的顶点坐标为m,m2+1
∵ 把该函数图象沿y轴向下平移5个单位后，得到的函数图象与x轴只有一个公共点，
∴ m2+1=5
解得m1=2,m2=−2
即m的值为±2
【答案】
证明：∵ ∠BAC＝90∘，∠EAD＝45∘，
∴ ∠BAE+∠DAC＝45∘，
∵ 将△ADC绕点A顺时针旋转90∘，得到△AFB，
∴ ∠BAF＝∠DAC，AF＝AD，CD＝BF，∠ABF＝∠ACD＝45∘，
∴ ∠BAF+∠BAE＝45∘＝∠FAE，
∴ ∠FAE＝∠DAE，AD＝AF，AE＝AE，
∴ △AEF≅△AED(SAS)，
∴ DE＝EF
（2）∵ AB＝AC＝22，∠BAC＝90∘，
∴ BC＝4，
∵ CD＝1，
∴ BF＝1，BD＝3，即BE+DE＝3，
∵ ∠ABF＝∠ABC＝45∘，
∴ ∠EBF＝90∘，
∴ BF2+BE2＝EF2，
∴ 12+(3−EF)2＝EF2，
∴ EF＝53
【考点】
旋转的性质
全等三角形的性质与判定
【解析】
（1）通过SAS证=AEFg=AED得4DE=L:F；
（2）先由2ABC是等腰直角三角形可得∠ABC=∠C=45∘ BC=4；通过旋转的性质可得△FBBACD，则得BF=CD=1∠ABF=∠C=45∘，继而得∠EBF=90∘ BE=(】}−EF）；在Rt△EBF中，根据勾股定理求得FE的长．
【解答】
证明：∵ ∠BAC＝90∘，∠EAD＝45∘，
∴ ∠BAE+∠DAC＝45∘，
∵ 将△ADC绕点A顺时针旋转90∘，得到△AFB，
∴ ∠BAF＝∠DAC，AF＝AD，CD＝BF，∠ABF＝∠ACD＝45∘，
∴ ∠BAF+∠BAE＝45∘＝∠FAE，
∴ ∠FAE＝∠DAE，AD＝AF，AE＝AE，
∴ △AEF≅△AED(SAS)，
∴ DE＝EF
（2）∵ AB＝AC＝22，∠BAC＝90∘，
∴ BC＝4，
∵ CD＝1，
∴ BF＝1，BD＝3，即BE+DE＝3，
∵ ∠ABF＝∠ABC＝45∘，
∴ ∠EBF＝90∘，
∴ BF2+BE2＝EF2，
∴ 12+(3−EF)2＝EF2，
∴ EF＝53
【答案】
证明：
∵ OA＝OC，
∴ ∠A＝∠ACO，
∵ ∠PCB＝∠A，
∴ ∠ACO＝∠PCB，
∵ AB是⊙O的直径，
∴ ∠ACO+∠OCB＝90∘，
∴ ∠PCB+∠OCB＝90∘，即OC⊥CP，
∵ OC是⊙O的半径，
∴ PC是⊙O的切线；
解∵ CP＝CA，
∴ ∠P＝∠A，
∴ ∠COB＝2∠A＝2∠P，
∵ ∠OCP＝90∘，
∴ ∠P＝30∘，
∵ OC＝OA＝2，
∴ OP＝2OC＝4，
∴ PC=42−22=23．
【考点】
圆周角定理
切线的判定与性质
【解析】
（1）欲证明PC是⊙O的切线，只要证明OC⊥PC即可；
（2）想办法证明∠P＝30∘即可解决问题．
【解答】
证明：
∵ OA＝OC，
∴ ∠A＝∠ACO，
∵ ∠PCB＝∠A，
∴ ∠ACO＝∠PCB，
∵ AB是⊙O的直径，
∴ ∠ACO+∠OCB＝90∘，
∴ ∠PCB+∠OCB＝90∘，即OC⊥CP，
∵ OC是⊙O的半径，
∴ PC是⊙O的切线；
解∵ CP＝CA，
∴ ∠P＝∠A，
∴ ∠COB＝2∠A＝2∠P，
∵ ∠OCP＝90∘，
∴ ∠P＝30∘，
∵ OC＝OA＝2，
∴ OP＝2OC＝4，
∴ PC=42−22=23．
【答案】
∵ 抛物线与y轴相交于点C(0, −3)，对称轴为直线x＝1
∴ c＝−3，−b2=1，即b＝−2，
∴ 二次函数解析式为y＝x2−2x−3；
结论四边形EFCD是正方形．
理由：如图，连接CE与DF交于点K．
∵ y＝(x−1)2−4，
∴ 顶点D(1, 4)，
∵ C、E关于对称轴对称，C(0, −3)，
∴ E(2, −3)，
∵ A(−1, 0)，
设直线AE的解析式为y＝kx+b，则−k+b=02k+b=−3 ，
解得k=−1b=−1 ，
∴ 直线AE的解析式为y＝−x−1．
∴ F(1, −2)，
∴ CK＝EK＝1，FK＝DK＝1，
∴ 四边形EFCD是平行四边形，
又∵ CE⊥DF，CE＝DF，
∴ 四边形EFCD是正方形．
【考点】
二次函数图象上点的坐标特征
抛物线与x轴的交点
二次函数的性质
待定系数法求二次函数解析式
【解析】
（1）抛物线与y轴相交于点C(0, −3)，对称轴为直线x＝1知c＝−3，−b2=1，据此可得答案；
（2）结论四边形EFCD是正方形．如图1中，连接CE与DF交于点K．求出E、F、D、C四点坐标，只要证明DF⊥CE，DF＝CE，KC＝KE，KF＝KD即可证明．
【解答】
∵ 抛物线与y轴相交于点C(0, −3)，对称轴为直线x＝1
∴ c＝−3，−b2=1，即b＝−2，
∴ 二次函数解析式为y＝x2−2x−3；
结论四边形EFCD是正方形．
理由：如图，连接CE与DF交于点K．
∵ y＝(x−1)2−4，
∴ 顶点D(1, 4)，
∵ C、E关于对称轴对称，C(0, −3)，
∴ E(2, −3)，
∵ A(−1, 0)，
设直线AE的解析式为y＝kx+b，则−k+b=02k+b=−3 ，
解得k=−1b=−1 ，
∴ 直线AE的解析式为y＝−x−1．
∴ F(1, −2)，
∴ CK＝EK＝1，FK＝DK＝1，
∴ 四边形EFCD是平行四边形，
又∵ CE⊥DF，CE＝DF，
∴ 四边形EFCD是正方形．组别(cm)
x<150
150≤x<155
155≤x<160
160≤x<165
x≥165
频数
2
23
52
18
5