初中数学人教版八年级下册18.2.1 矩形评课ppt课件

这是一份初中数学人教版八年级下册18.2.1 矩形评课ppt课件，共23页。PPT课件主要包含了课堂讲解，课时流程，矩形的四个角都是直角，对角线，矩形的性质，知识点，有直角的个数判定矩形，知识小结，矩形的判定方法等内容，欢迎下载使用。
由对角线的关系判定矩形由直角的个数判定矩形
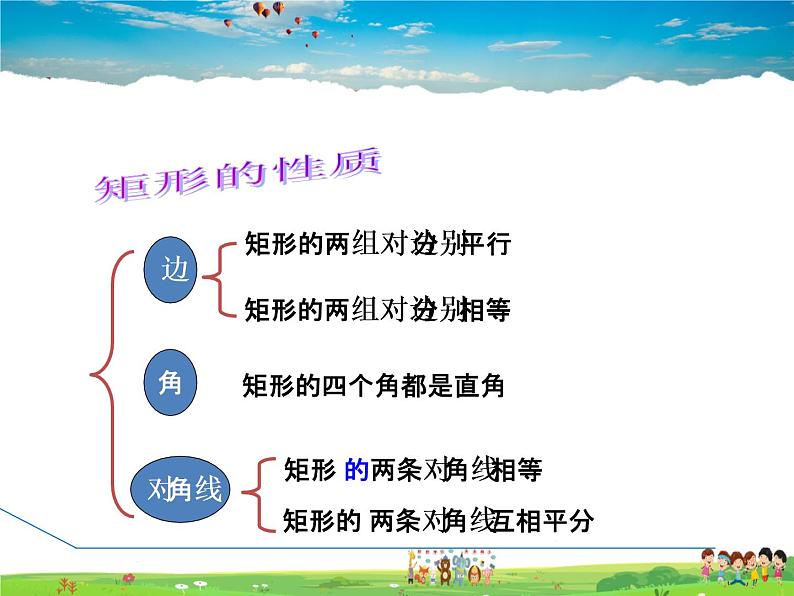
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形 的两条对角线相等
由对角线的关系判定矩形
我们知道，矩形的对角线相等. 反过来，对角线相等的平行四边形是矩形吗？ 工人师傅在做门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形.你知道其中的道理吗？
可以发现并证明矩形的一个判定定理： 对角线相等的平行四边形是矩形.警示：两条对角线相等的四边形不一定是矩形，这个 四边形必须是平行四边形才可以.
例1 如图，在▱ABCD中，对角线AC，BD相交于点O， 且OA=OD，∠OAD=50°.求∠OAB的度数.
∵四边形ABCD是平行四边形，∴OA=OC= AC，OB=OD= BD.又 OA=OD，∴ AC=BD.∴四边形ABCD是矩形.∴ ∠DAB=90°. 又∠OAD=50°，∴∠OAB=40°.
用对角线相等的平行四边形是矩形判定一个四边形是矩形必须满足两个条件：一是对角线相等，二是四边形是平行四边形．
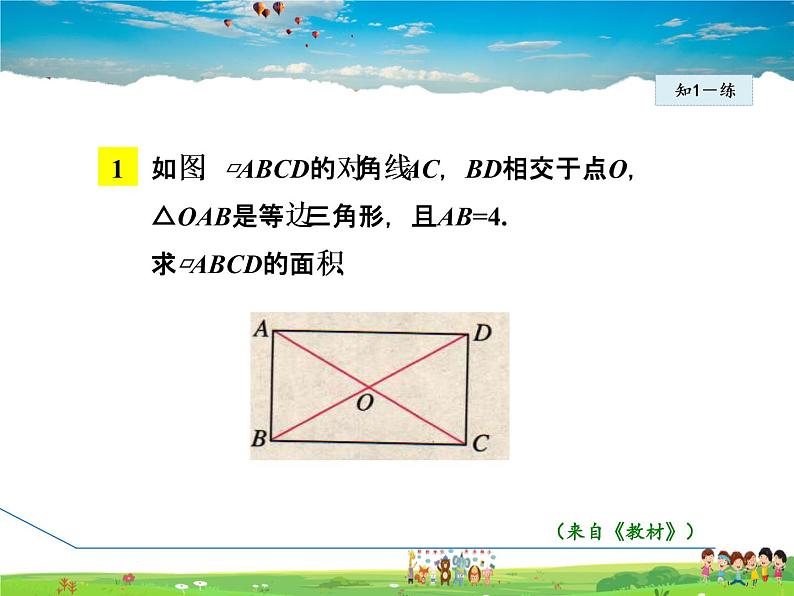
1 如图，▱ABCD的对角线AC，BD相交于点O， △OAB是等边三角形，且AB=4. 求▱ABCD的面积.
因为四边形ABCD是平行四边形，所以OA＝OC，OB＝OD.又因为△OAB是等边三角形，所以OA＝OB＝AB.所以OA＝OB＝OC＝OD.所以AC＝BD，所以▱ABCD是矩形．又因为AB＝4，所以AC＝8，所以BC＝所以S矩形ABCD＝AB·BC＝4×
如图，要使▱ABCD成为矩形，需添加的条件是(　　)A．AB＝BC B．AO＝BOC．∠1＝∠2 D．AC⊥BD
【中考·黑龙江】如图，在▱ABCD中，延长AD到点E，使DE＝AD，连接EB，EC，DB，请你添加一个条件______________________，使四边形DBCE是矩形．
EB＝DC(答案不唯一)
前面我们研究了矩形的四个角，知道它们都是直角. 它的逆命题成立吗？即四个角都是直角的四边形是矩形吗？进一步，至少有几个角是直角的四边形是矩形？
(1)根据矩形的定义，有一个角是直角的平行四边形 是矩形．如果不通过平行四边形，能根据四边形 中直角的个数，直接由四边形来判定它是矩形吗? 有几个角是直角的四边形是矩形呢? 矩形的四个角都是直角.反过来，四个角都是直角 的四边形是矩形.
已知：如图所示，在四边形ABCD中， ∠A=∠B=∠C=90°． 求证：四边形ABCD是矩形．
∵∠A=∠B=∠C=90°， ∠A+∠B=180°， ∠B+∠C=180°，∴AD∥BC， AB∥CD.∴四边形ABCD是平行四边形.∵∠A=90°.∴ ▱ABCD是矩形.
有三个角是直角的四边形是矩形.
例2 如图，▱ABCD的四个内角的平分线分别相交于 点E，F，G，H.求证：四边形EFGH是矩形.
要证明四边形EFGH是矩形，由于已知ABCD的四个内角的平分线分别相交于点E，F，G，H，因此可选用“有三个角是直角的四边形是矩形”来证明．
∵AB∥CD，∴∠ABC＋∠BCD＝180°.∵BG平分∠ABC，CG平分∠BCD，∴∠GBC＋∠GCB＝ ∠ABC＋ ∠BCD ＝ ×180°＝90°，∴∠BGC＝90°. 同理可得∠AFB＝∠AED＝90°.∴∠GFE＝∠FEH＝∠FGH＝90°.∴四边形EFGH是矩形．
本题目中的图形是建立在四边形基础上，而条件中又涉及角的关系，一般采用“角的方法”来判定矩形．
下列命题中，真命题有(　　)(1)对角线互相平分的四边形是矩形(2)三个角的度数之比为1：3 ：4的三角形是直角三角形(3)对角互补的平行四边形是矩形(4)三边之比为1： ：2的三角形是直角三角形A．1个 B．2个 C．3个 D．4个
如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是(　　)A．AB∥DC B．AC＝BD C．AC⊥BD D．AB＝DC
【中考·上海】已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是(　　)A．∠BAC＝∠DCA B．∠BAC＝∠DACC．∠BAC＝∠ABD D．∠BAC＝∠ADB
1. 有一个角是直角的平行四边形2. 对角线相等的平行四边形3. 有三个角是直角的四边形