人教版八年级上册13.3.1 等腰三角形评课课件ppt

这是一份人教版八年级上册13.3.1 等腰三角形评课课件ppt，共22页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点等内容，欢迎下载使用。

等腰三角形边角性质：等边对等角等腰三角形的轴对称性：“三线合一”
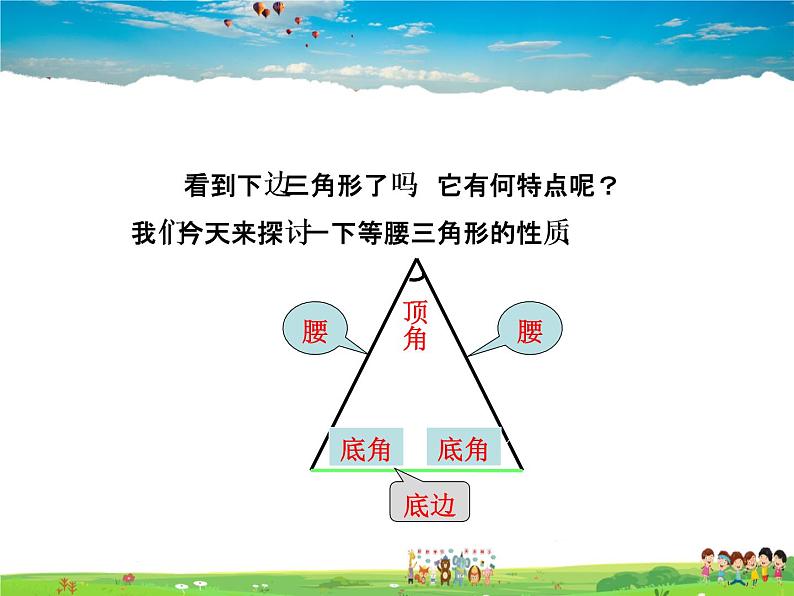
看到下边三角形了吗，它有何特点呢？我们今天来探讨一下等腰三角形的性质.
等腰三角形边角性质：等边对等角
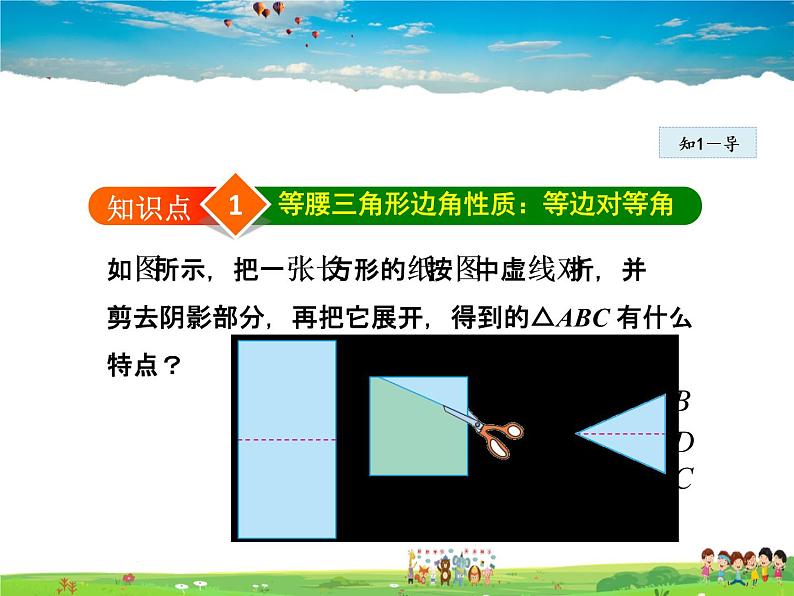
如图所示，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC 有什么特点？
仔细观察自己剪出的等腰三角形纸片，你能发现这 个等腰三角形有什么特征吗？
等腰三角形的特征:(1)等腰三角形的两个底角相等；(2)等腰三角形的顶角平分线、底边上的中线、底 　　 边上的高互相重合．
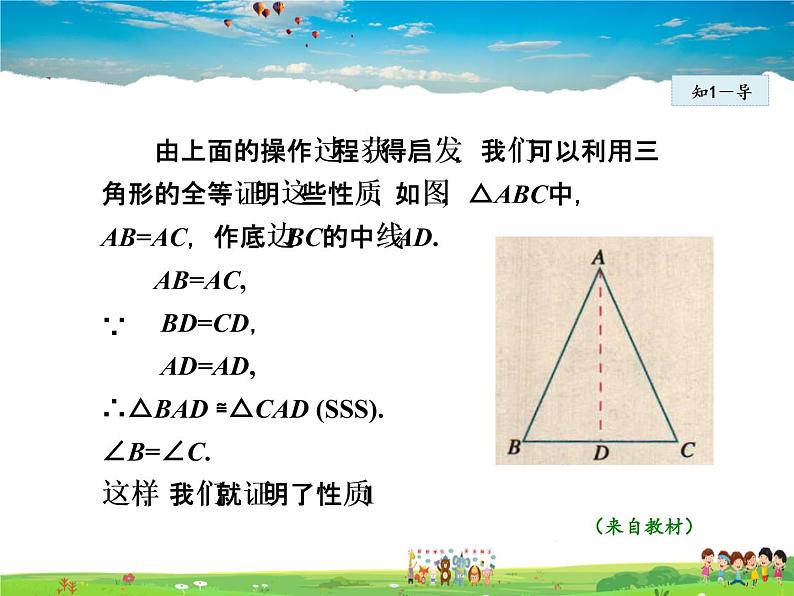
由上面的操作过程获得启发，我们可以利用三角形的全等证明这些性质. 如图, △ABC中，AB=AC，作底边BC的中线AD. AB=AC, BD=CD， AD=AD,∴△BAD ≌△CAD (SSS).∠B=∠C.这样，我们就证明了性质1
我们可以发现等腰三角形的性质：性质1 等腰三角形的两个底角相等（简写成“等边对顶角”.
例1 如图，在△ABC中，AB=AC，点D在AC上，且 BD=BC=AD,求△ABC各角的度数. 解：∵ AB=AC, BD=BC=AD, ∴ ∠ABC=∠C=∠BDC, ∠A=∠ABD(等边对等角）. 设∠A=x，则 ∠BDC=∠A+∠ABD=2x， 从而∠ABC=∠C=∠BDC=2x. 于是在△ABC中，有 ∠A+ ∠ABC=∠C=x+2x=2x=180°. 解得x=36°. 所以，在△ABC 中，∠A=36°, ∠ABC=∠C=72°.
如图，在下列等腰三角形中，分别求出它们的底 角的度数.
解：(1)72°; (2)30°.
(中考•盐城)若等腰三角形的顶角为40°，则它的底角度数为(　　) A．40° B．50° C．60° D．70°
(中考•湘西州)如图，等腰三角形ABC中，AB＝AC，BD平分∠ABC，∠A＝36°，则∠1的度数为(　　) A．36° B．60° C．72° D．108°
(中考•广西)如图，在△ABC中，AB＝AC，∠BAC＝100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE＝(　　) A．80° B．60° C．50° D．40°
等腰三角形的轴对称性：“三线合一”
探究 把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角. 由这些重合的线段和角，你能发现等腰三角形的性质吗？说一说你的 猜想. 在一张白纸上任意画一个等腰三角形，把它剪下来，请你试着折一 折.你的猜想仍然成立吗？
性质2 等腰三角形的顶角平分线、底边上的中线、 底边上的高相互重合（简写成“三线合一”）
例2 如图，在△ABC中，AB＝AC，AD是BC边上 的中线，∠ABC的平分线BG交AC于点G，交 AD于点E，EF⊥AB，垂足为F. (1)若∠BAD＝25°，求∠C的度数； (2)求证：EF＝ED.
(1)解：∵AB＝AC，AD是BC边上的中线， ∴∠BAD＝∠CAD，∴∠BAC＝2∠BAD＝50°. ∵AB＝AC， ∴ ∠C＝∠ABC ＝ (180°－ ∠A) ＝ (180°－50°)＝65°.(2)证明：∵AB＝AC，AD是BC边上的中线， ∴ED⊥BC， 又∵BG平分∠ABC，EF⊥AB， ∴EF＝ED.
(1)等腰三角形的“三线合一”的性质是证明角相等、 线段相等和垂直关系的既重要又简便的方法；因 为题目的证明或计算所求结果大多都是单一的， 所以“三线合一”的性质的应用也是单一的，一 般得出一个结论，因此应用要灵活．(2)在等腰三角形中，作“三线”中“一线”，利用 “三线合一”是等腰三角形中常用的方法．
1 (中考•苏州)如图，在△ABC中，AB＝AC，D为 BC的中点，∠BAD＝35°，则∠C的度数 为(　　) A．35° B．45° C．55° D．60°
2 如图，在△ABC中，AB＝AC，点D是BC边的中 点，点E在AD上，那么下列结论不一定正确的 是 (　　) A．AD⊥BC B．∠EBC＝∠ECB C．∠ABE＝∠ACE D．AE＝BE
3 如图，在△ABC中，AB＝AC，点D、E在 BC上，连接AD、AE，如果只添加一个条件使 ∠DAB＝∠EAC，则添加的条件不能为(　　) A．BD＝CE B．AD＝AE C．DA＝DE D．BE＝CD
这节课我们主要探讨了等腰三角形的性质，并对性质作了简单的应用．等腰三角形是轴对称图形，它的两个底角相等（等边对等角），等腰三角形的对称轴是它顶角的平分线，并且它的顶角平分线既是底边上的中线，又是底边上的高．