2022届浙江省杭州地区（含周边）重点中学高三上学期期中考试 数学（word版含答案）练习题

绝密★考试结束前

2021学年第一学期期中杭州地区(含周边)重点中学

高三年级数学学科试题

考生须知：

1.本卷满分150分，考试时间120分钟；

2.答题前，在答题卷密封区内填写班级、学号和姓名：座位号写在指定位置；

3.所有答案必须写在答题卷上，写在试卷上无效；

4.考试结束后，只需上交答题卷。

选择题部分

一、选择题：本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合A＝{x|1≤x≤3}，B＝{x|0<x<2}，则A∩B＝

A.{x|1≤x<2}     B.{x|0<x≤3}     C.{x|1≤x≤2}     D.{x|0≤x≤2}

2.设(1＋2i)·z＝3＋i(i为虚数单位)，则|z|＝

A.     B.     C.3     D.2

3.若实数x，y满足约束条件，则z＝x－2y的取值范围是

A.[1，5]     B.[－1，5]     C.[－5，－1]     D.[－5，5]

4.(1－2x)6展开式中，x3的系数为

A.20     B.－20     C.160     D.－160

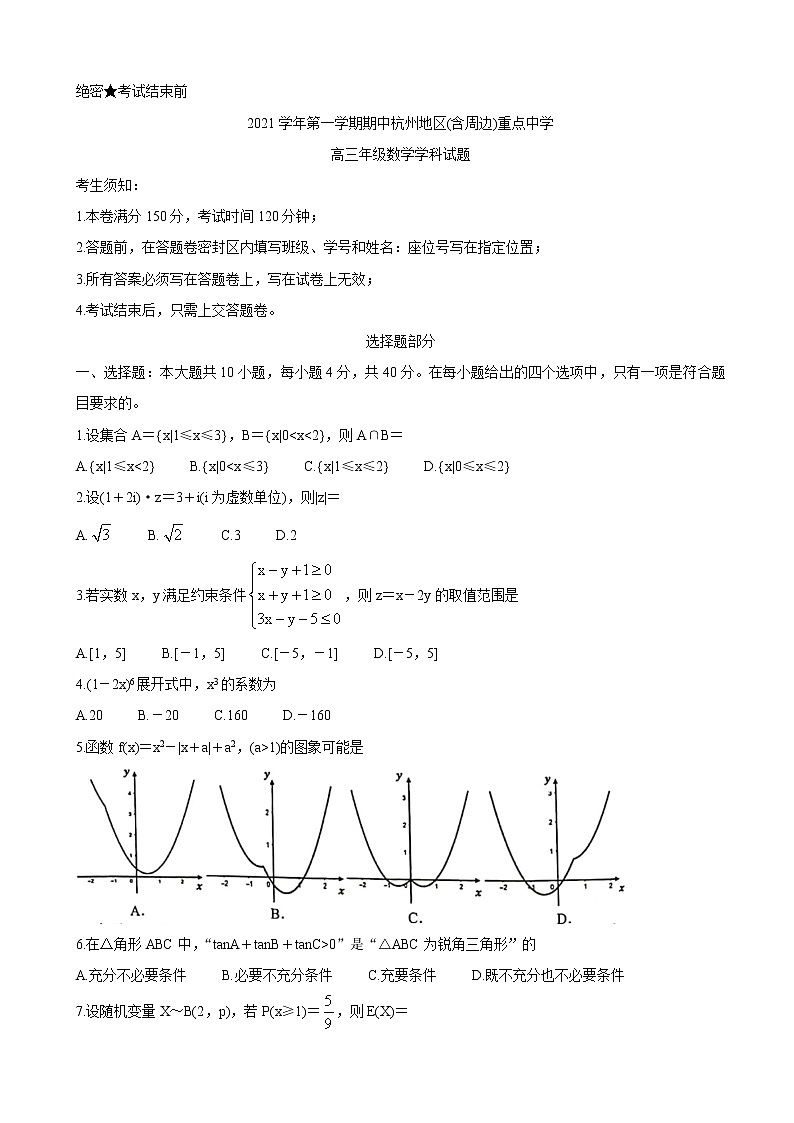
5.函数f(x)＝x2－|x＋a|＋a2，(a>1)的图象可能是

6.在△角形ABC中，“tanA＋tanB＋tanC>0”是“△ABC为锐角三角形”的

A.充分不必要条件     B.必要不充分条件     C.充要条件     D.既不充分也不必要条件

7.设随机变量X～B(2，p)，若P(x≥1)＝，则E(X)＝

A.     B.     C.     D.1

8.对于平面内不共线的四点O、A、B、C，若存在一组正实数λ1、λ2、λ3，使得，则三个角∠AOB、∠BOC、∠COA

A.都是钝角     B.至少有两个钝角     C.恰有两个钝角     D.至多有两个钝角

9.若对任意的x1，x2∈[1，＋∞)，当x2>x1时，恒有aln<2(x2－x1)成立，则实数a的取值范围是

A.(－∞，0]     B.(－∞，1]     C.(－∞，2]     D.(－∞，3]

10.已知数列{an}，{bn}，数列{cn}满足cn＝，n∈N*。若an＝4n－1，且对任意n∈N*，cn＋1>cn恒成立，则{bn}可能为

A.bn＝4n     B.bn＝2n     C.bn＝3n     D.bn＝3n＋1

非选择题部分

二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。

11.《九章算术》是我国古代内容极为丰富的数学名著，其中有这样一个问题：“今有宛田，下周三十步，径十六步。问为田几何？”其意思为：“有一块扇形的田，弧长为30步，其所在圆的直径为16步，问这块田的面积是多少平方步？”该问题的答案为          平方步。

12.若a＝log23，3b＝2，则2a＋2－a＝          ，ab＝          。

13.在平面直角坐标系中，A(0，2)，B(0，4)，在x轴正半轴有点C(t，0)，则tan∠ACB的最大值为          ，此时t＝          。

14.己知正整数a，b满足2<a<b<10，则的最大值为          ，最小值为          。

15.已知a，b为单位向量，且，设向量2＋与向量的夹角为θ，则cosθ＝       。

16.男生甲和女生乙及另外2男2女共6位同学排成一排拍照，要求男女生相间且甲和乙相邻，共有          种不同排法。

17.函数f(x)＝2x－x2的零点个数为         ，若函数f(x)＝ax－x2(a>1)恰有两个零点，则a＝          。

三、解答题：本大题共5小题，共74分。解答应写出文字说明、证明过程或演算步骤。

18.(本题满分14分)

设函数f(x)＝sinx－cosx，(x∈R)

(I)求y＝[f(x)]2的最大值和对称中心；

(II)f'(x)为f(x)的导函数，若f'(x0)＝2f(x0)，求sin2x0＋cos2x0＋tan(＋x0)的值。

19.(本题满分15分)

如图，在三棱锥P－ABC中，AB＝BC＝2，AP＝PC，∠ABC＝60°，AP⊥PC。

(I)求证：AC⊥BP；

(II)若直线BP与平面ABC成30°角，求BP。

20.(本题满分15分)

已知数列{an}，a1＝1，且满足an＋1－2an－1＝0。数列{bn}满足b1＝1，数列的前n项和为n2＋n。

(I)证明：数列{an＋1}为等比数列并求{an}的通项公式；

(II)求数列{bn}的通项公式。

21.(本题满分1s5分)

已知点A1(－，0)，A2(，0)，直线PA1，PA2的斜率之积为－，设点P的轨迹为曲线C。

(I)求曲线C的轨迹方程；

(II)若抛物线y2＝2px(p>0)与曲线C交于点A，B，设M(－1，0)，求△ABM面积最大时p的值。

22.(本题满分15分)

已知f(x)＝，直线l为曲线y＝f(x)在(t，f(t))处的切线，直线l与曲线y＝f(x)相交于点(s，f(s))且s<1。

(I)求t的取值范围；

(II)①证明：lnx≤1＋·(x－e)－·(x－e)2＋·(x－e)3；

②证明：s>t－3tlnt。