初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数复习ppt课件

这是一份初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数复习ppt课件，共19页。PPT课件主要包含了导入课题，复习目标，yx2+2x-3，转化成，向左平移4，向下平移3，基础巩固，综合应用，y-x2+4x+5，拓展延伸等内容，欢迎下载使用。

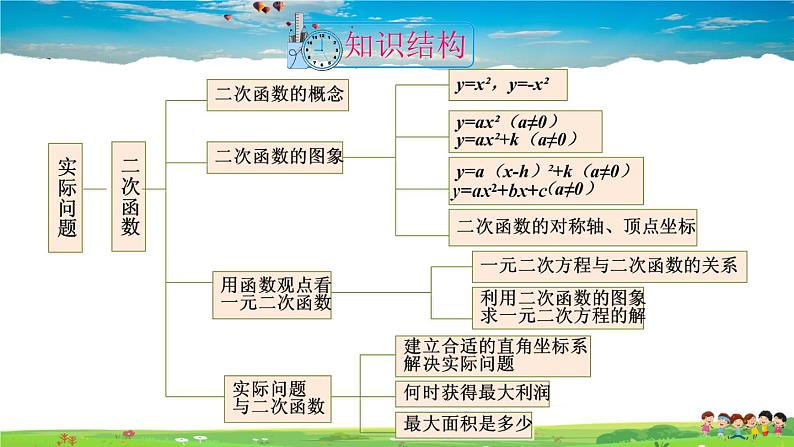
　　本章我们学习了什么内容？
　　那么大家掌握得如何呢？这节课我们一起来作一个回顾总结，检阅学习成果.
(1)进一步加深对二次函数的概念、图象及其性质的理解.(2)能感受函数思想、建模思想和转化思想.
专题训练一 二次函数的图象与性质
已知：抛物线y=2x2-4x-6.(1)直接写出抛物线的开口方向、对称轴、顶点坐标；(2)求抛物线与坐标轴的交点坐标；(3)当x为何值时，y随x的增大而增大？
将抛物线解析式转化成顶点式：y=2x2-4x-6=2(x-1)2-8
解:(1)开口向上，对称轴为直线x=1,顶点坐标为(1，-8).(2)令y=0,得2x2-4x-6=0,解得x1=-1,x2=3.令x=0,得y=-6.所以抛物线与x轴的交点坐标为(-1,0)，(3,0)，与y轴的交点坐标为(0，-6).(3)当x≥1时，y随x的增大而增大.
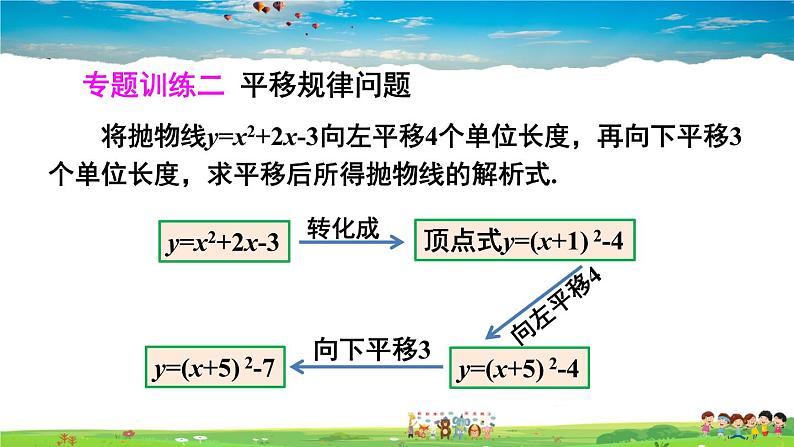
将抛物线y=x2+2x-3向左平移4个单位长度，再向下平移3个单位长度，求平移后所得抛物线的解析式.
专题训练二 平移规律问题
顶点式y=(x+1) 2-4
y=(x+5) 2-4
y=(x+5) 2-7
（辽宁盘锦）如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴是直线x=-2.关于下列结论：①ab<0；②b2-4ac>0；③9a-3b+c<0；④b-4a=0；⑤方程ax2+bx=0的两个根为x1=0, x2=-4. 其中正确的结论有（ ）A.①③④ B.②④⑤C.①②⑤ D.②③⑤
专题训练三 字母系数及相关代数式正负的判断
（黑龙江牡丹江中考）已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1,x2(x1专题训练四 二次函数与一元二次方程的关系
1.已知二次函数y=-x2+4x+5，则当x= 时，其最大值为 .2.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(-1，-3.2)及部分图象(如图),由图象可知关于x的方程ax2+bx+c=0的两个根分别是x1=1.3和x2= .
3.设A(-2,y1)，B(1,y2)，C(2,y3)是抛物线y=-(x+1)2+a上的三点，则y1，y2，y3的大小关系为( )A．y1＞y2＞y3B．y1＞y3＞y2C．y3＞y2＞y1D．y3＞y1＞y2
(1)求抛物线的开口方向、对称轴及顶点坐标；(2)求抛物线与x轴、y轴的交点坐标；
(2) 与x轴的交点： 与y轴的交点：
开口:向上，对称轴:x=3,顶点坐标:(3，-7).
(3)画出函数图象(草图)；
(4)根据图象说出：x为何值时，y随x的增大而增大？x为何值时,y随x的增大而减小？
当x>3时，y随x的增大而增大.当x<3时，y随x的增大而减小.
5.如图,已知抛物线y=ax2+bx+c过点C(3,8),与x轴交于A(-1,0)，B两点,与y轴交于点D(0,5)．(1)求该二次函数的关系式；(2)求该抛物线的顶点M的坐标,并求四边形ABMD的面积．
解:(1)∵抛物线过点(3,8)，(-1,0)，(0,5)， ∴该二次函数关系式为y=-x2+4x+5
(2)顶点M的坐标为(2，9)，对称轴为直线x=2,则B点坐标为(5，0)，过M作MN⊥AB于N，则S四边形ABMD =S△AOD+S梯形DONM +S△MNB
故四边形ABMD的面积为30.
6.某商场将进货价为30元的书包以40元售出，平均每月能售出600个，调查表明：这种书包的售价每上涨1元，其销售量就减少10个.(1)请写出每月售出书包的利润y(元)与每个书包涨价x(元)间的函数关系式；
y=(40+x-30)(600-10x)
=-10x2+500x+6000.
(2)设某月的利润为10000元，10000元的利润是否为该月最大利润？如果是，请说明理由；如果不是，请求出最大利润，并指出此时书包的售价应定为多少元. 
(2)10000元不是最大利润，y =-10x2+500x+6000 =-10(x-25)2+12250.当x=25时有最大利润，即售价为65元时，有最大利润12250元.