



初中数学人教版八年级下册18.1.2 平行四边形的判定课堂教学课件ppt
展开1.知道平行四边形的四种判定方法及推理格式.2.能用这些判定方法证明一个四边形是平行四边形.
平行四边形有哪些性质?
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
问题 如何寻找平行四边形的判定方法?
勾股定理的逆定理
我们来回顾一下直角三角形的判定定理是怎么来的.
逆向思考 提出猜想
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
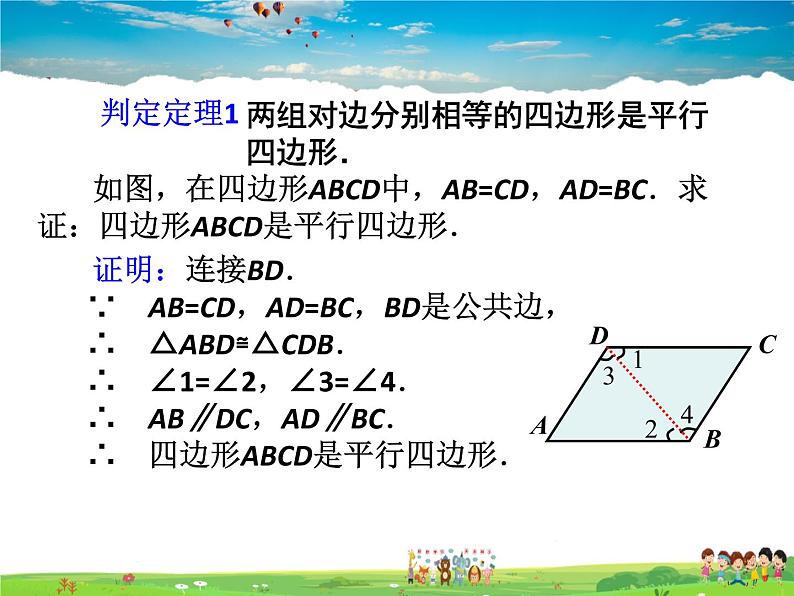
证明:连接BD. ∵ AB=CD,AD=BC,BD是公共边, ∴ △ABD≌△CDB. ∴ ∠1=∠2,∠3=∠4. ∴ AB∥DC,AD∥BC. ∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
证明:∵ 多边形ABCD是四边形, ∴∠A+∠B+∠C+∠D=360°. 又∵∠A=∠C,∠B=∠D, ∴∠A+∠B=180°, ∠B+∠C=180°. ∴AD∥BC,AB∥DC. ∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
证明:∵ OA=OC,OB=OD,∠AOD=∠COB, ∴ △AOD≌△COB. ∴ ∠OAD=∠OCB. ∴ AD∥BC. 同理 AB∥DC. ∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中, AC,BD相交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
现在,我们一共有哪些判定平行四边形的方法呢? 定义:两组对边分别平行的四边形叫做平行四边形. 判定定理: (1)两组对边分别相等的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形.
如图,AB=DC=EF,AD=BC,DE=CF. 图中有哪些互相平行的线段?
解:AB∥CD∥EF,AD∥BC,DE∥CF.
例3 如图, ABCD的对角线AC,BD相交于点O,E,F是AC 上的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形, ∴AO=CO,BO=DO. ∵AE=CF, ∴AO-AE=CO-CF,即EO=FO. 又BO=DO,∴四边形BFDE是平行四边形.
平行四边形判定定理的应用
1.如图,AB=DC=EF,AD=BC,DE=CF.求证:AB∥EF.
证明:∵ AB=DC,AD=BC, ∴ 四边形ABCD是平行四边形. ∴ AB∥DC. 又∵ DC=EF,DE=CF, ∴ 四边形DCFE也是平行四边形. ∴ DC∥EF.∴ AB∥EF.
2.如图, ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点. 求证:BE=DF.
证明:∵四边形ABCD是平行四边形,∴DO=OB,AO=OC,又E,F分别是OA,OC的中点,∴EO=FO,在△DOF与△BOE中,DO=BO,∠DOF=∠BOE,FO=EO,∴△DOF≌△BOE,∴BE=DF.
1.如图,△ABC平移后得到△DEF,则图中的平行四边形分别有____________________________.
2.如图,DB∥AC,DB= AC,E是AC的中点,求证:BC=DE.
证明:∵E为AC的中点,DB= AC∴DB=CE. 又∵DB∥AC,即DB∥CE,∴四边形BCED为平行四边形,∴BC=DE.
人教版八年级下册18.1.2 平行四边形的判定课前预习ppt课件: 这是一份人教版八年级下册18.1.2 平行四边形的判定课前预习ppt课件,共19页。PPT课件主要包含了知识回顾,学习目标,对边相等,对角线互相平分,对角相等,课堂导入,新知探究,证明连接AC,∴ADBC,∴ABCD等内容,欢迎下载使用。
初中数学人教版八年级下册18.1.2 平行四边形的判定课文内容ppt课件: 这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定课文内容ppt课件,共26页。PPT课件主要包含了平行四边形的性质,1从边看,2从角看,3从对角线看,对角线互相平分,平行四边形的判定方法,一直是,命题1,连接AC,命题2等内容,欢迎下载使用。
初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定备课ppt课件: 这是一份初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定备课ppt课件,共20页。PPT课件主要包含了学习目标,知识讲解,三角形的中位线,知识点1,所以EF=DG,你还想到了什么,即学即练,随堂练习,解OB2OD,拓展练习等内容,欢迎下载使用。













