冀教版九年级下册30.5 二次函数与一元二次方程的关系评课ppt课件

这是一份冀教版九年级下册30.5 二次函数与一元二次方程的关系评课ppt课件，共15页。PPT课件主要包含了知识回顾，巩固练习，新课探究，延伸拓展，b2-4ac，复习提问，自主学习一，想一想填一填，得a-1，课堂小结等内容，欢迎下载使用。

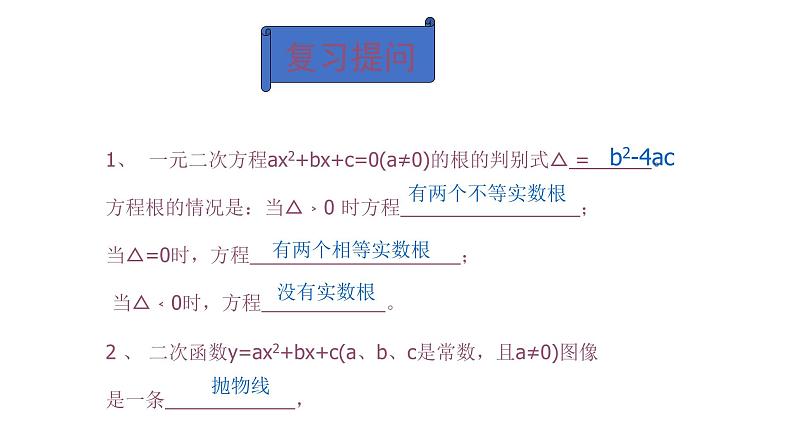
1、 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。方程根的情况是：当△﹥0 时方程 ；当△=0时，方程 ； 当△﹤0时，方程 。
2 、 二次函数y=ax2+bx+c(a、b、c是常数，且a≠0)图像是一条 ，
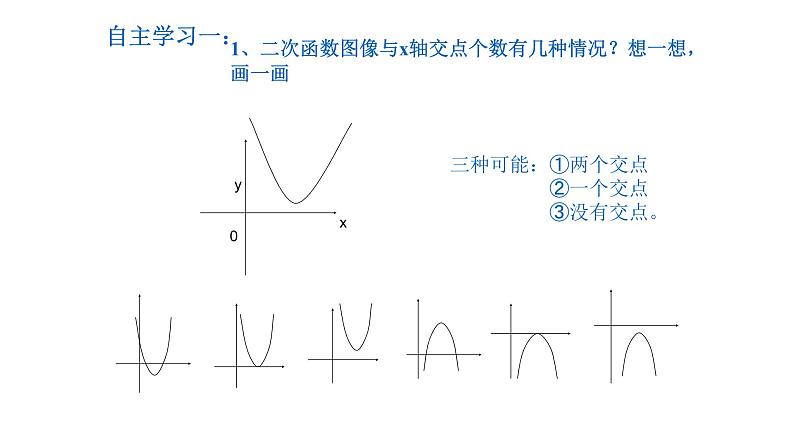
1、二次函数图像与x轴交点个数有几种情况？想一想，画一画
三种可能：①两个交点 ②一个交点 ③没有交点。
与x轴交点的横坐标是当y=0时自变量x的值 即方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点坐标与一元二次方ax2+bx+c=0的根有什么关系?
. 二次函数y=ax2+bx+c的图象和x轴交点的个数 与一元二次方程ax2+bx+c=0的根有什么关系?
自主学习二： 二次函数图象和x轴交点坐标与 一元二次方程的根有什么关系?
y=x2+2x与 x轴交点
X1 =-2 X2 =0
(-2,0) (0,0）
x2+2x=0方程的根是
交点的横坐标是一元二次方程的根
（2, 0）（4,0 ）
X1 =2 X2 =4
y=x2-6x+8与x轴交点是
x2-6x+8=0方程的根是
2.抛物线y=x2-4x+4与轴有 个交点，坐标是 。3.抛物线y=0.5x2-x+3与x轴的交点情况是（ ） A 两个交点 B 一个交点 C 没有交点 D 画出图象后才能说明
1 . 若方程ax2+bx+c=0的根为x1=-2和x2=3，则二次函数 y=ax2+bx+c的图象与x轴交点坐标是 。
（-2，0）、（3，0）
4 不画图象，求抛物线y=x2-3x-4与x轴的交点坐标。
解：∵解方程x2-3x-4=0得： x1=-1，x2=4 ∴抛物线y=x2-3x-4与x轴的交点坐标是： (-1，0)和(4，0)
5.若函数 图象与x 轴是只有一个公共点,求m的值.
解：∵ 图象与x 轴是只有一个公共点 则△=0 即 36-4m=0 ∴ m=9
设所求的二次函数为　y=a(x＋1)(x－2）
点M( 0,2 )在抛物线上
所以：a(0+1)(0-2)=2
故所求的抛物线为 y=- (x＋1)(x-2)
即：y=－x2+x+2
思考： 你能用什么方法做呢? 哪个方法更好?
用交点式求二次函数的解析式
2. 二次函数与一元二次方程的关系
1.二次函数y=ax2+bx+c与X轴交点个数的确定
3.用交点式求二次函数表达式