2020-2021学年第一章 全等三角形1.3 探索三角形全等的条件集体备课ppt课件

这是一份2020-2021学年第一章 全等三角形1.3 探索三角形全等的条件集体备课ppt课件，共12页。PPT课件主要包含了合作探究，归纳总结，∠B∠E，或∠A∠D，或ACDF，ASA，AAS，SAS，ABDE可以吗，AB∥DE等内容，欢迎下载使用。

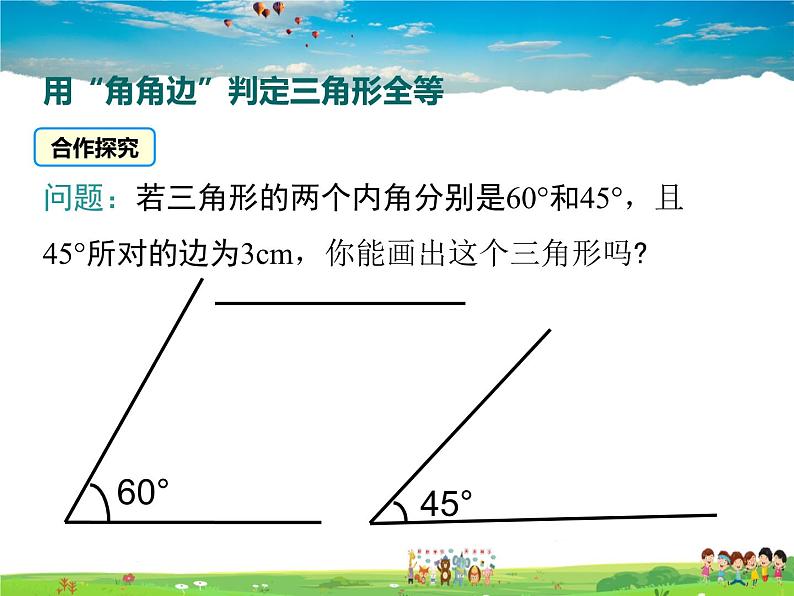
问题：若三角形的两个内角分别是60°和45°，且45°所对的边为3cm，你能画出这个三角形吗?
用“角角边”判定三角形全等
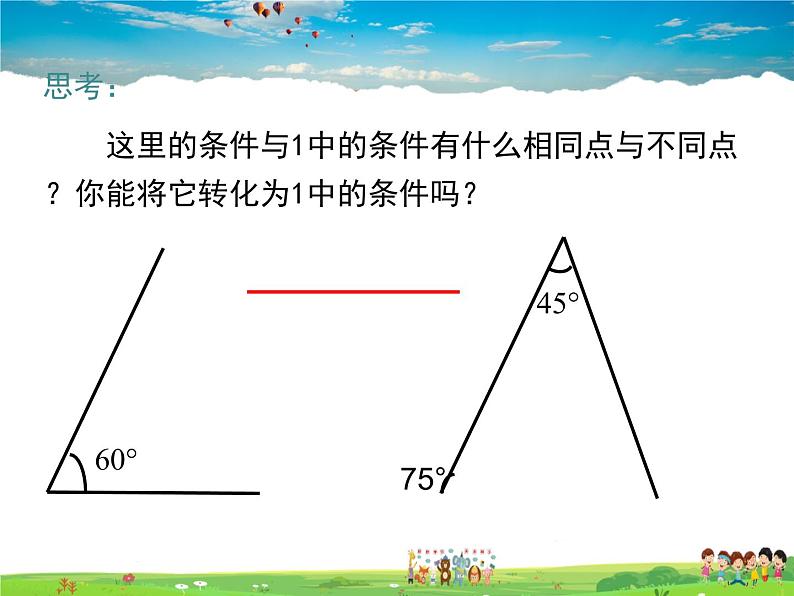
这里的条件与1中的条件有什么相同点与不同点？你能将它转化为1中的条件吗？
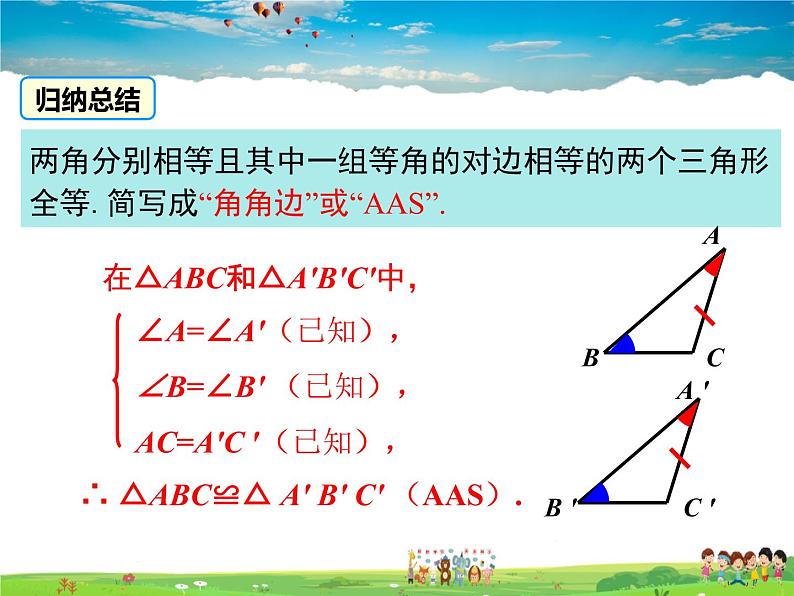
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
例1 如图，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E.试说明：(1)△BDA≌△AEC；
解：(1)∵BD⊥m，CE⊥m，∴∠ADB＝∠CEA＝90°，∴∠ABD＋∠BAD＝90°.∵AB⊥AC，∴∠BAD＋∠CAE＝90°，∠ABD＝∠CAE.在△BDA和△AEC中，
∠ADB=∠CEA=90°， ∠ABD＝∠CAE,AB＝AC，
∴△BDA≌△AEC(AAS).
(2)DE＝BD＋CE.
∴BD＝AE，AD＝CE，∴DE＝DA＋AE＝BD＋CE.
解：∵△BDA≌△AEC,
方法总结：利用全等三角形可以解决线段之间的关系，比如线段的相等关系、和差关系等，解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化．
例2.如图,已知AB=AC,AD=AE.求证:△BOD≌△COE.
1.如图∠ACB=∠DFE，BC=EF，那么应补充一个条件 ，才能使△ABC≌△DEF （写出一个即可）.
2.已知：如图， AB⊥BC，AD⊥DC，∠1=∠2, 试说明：AB=AD.
解： ∵ AB⊥BC，AD⊥DC，
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中，
∴ △ABC≌△ADC（AAS)，
3.如图①,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B、C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:BD=CE+DE.(2)若直线AE绕点A旋转到如图②的位置(BDCE)时,其余条件不变,则BD与DE、CE的关系如何?请直接写出结果,不需证明.(4)归纳上述(1)(2)(3)问,请用简洁的语言表达BD、DE、CE的关系.
(3)解:BD=DE-CE.(4)解:归纳(1)(2)(3)可知,结论表述为:当点B、C在AE异侧时,BD=DE+CE;当点B、C在AE同侧时,BD=DE-CE.