苏科版八年级上册2.5 等腰三角形的轴对称性背景图课件ppt

这是一份苏科版八年级上册2.5 等腰三角形的轴对称性背景图课件ppt，共20页。PPT课件主要包含了温故知新，探索活动一，说一说，例题讲解，∴ABAC，探索活动二，轴对称图形3条，三边相等，三个角都等于60度，三线合一3条等内容，欢迎下载使用。

1.等腰三角形有哪些性质？
2.在一个三角形中，如果有两个角相等，那么这两个角所对的边的大小有什么关系？
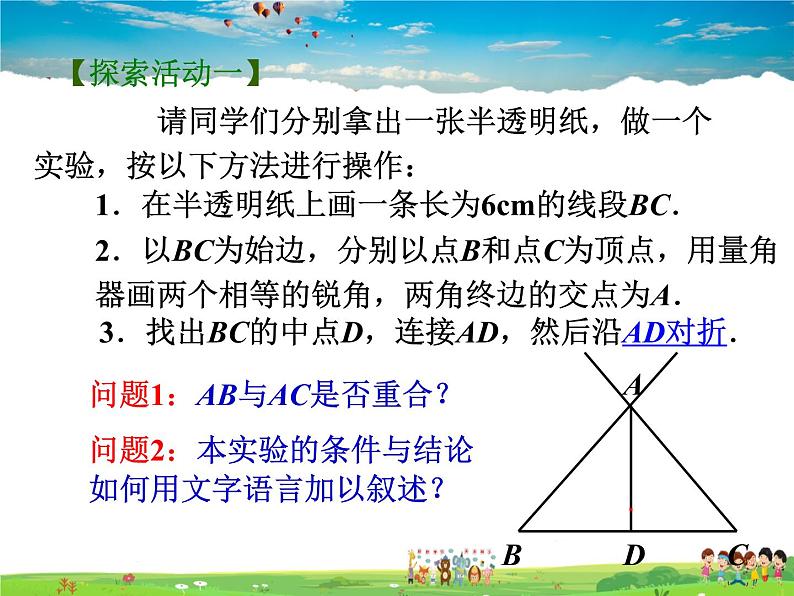
　　 请同学们分别拿出一张半透明纸，做一个实验，按以下方法进行操作：
1．在半透明纸上画一条长为6cm的线段BC．
2．以BC为始边，分别以点B和点C为顶点，用量角器画两个相等的锐角，两角终边的交点为A．
3．找出BC的中点D，连接AD，然后沿AD对折．
问题1：AB与AC是否重合？
问题2：本实验的条件与结论如何用文字语言加以叙述？
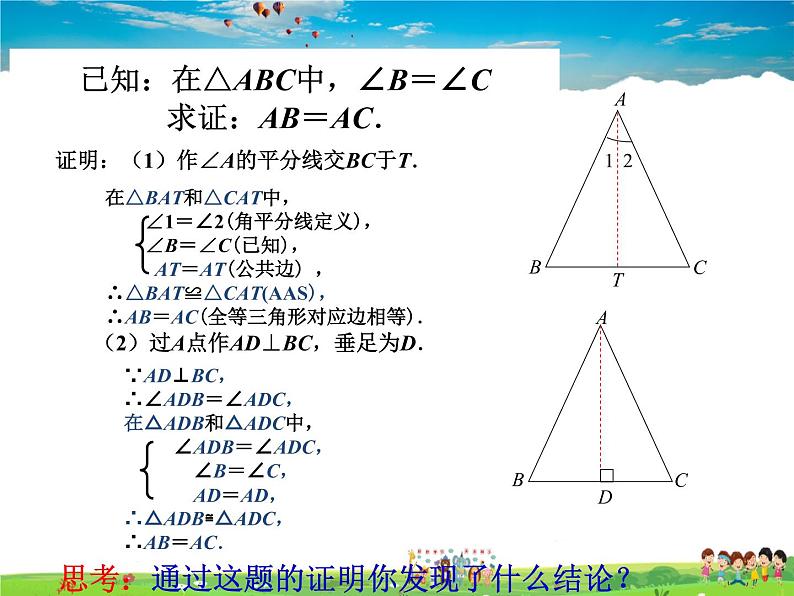
在△BAT和△CAT中，　 ∠1＝∠2(角平分线定义)， ∠B＝∠C(已知)， AT＝AT(公共边) ， ∴△BAT≌△CAT(AAS)，∴AB＝AC(全等三角形对应边相等)．
已知：在△ABC中，∠B＝∠C 求证：AB＝AC．
证明：（1）作∠A的平分线交BC于T．
（2）过A点作AD⊥BC，垂足为D．
∵AD⊥BC，∴∠ADB＝∠ADC，在△ADB和△ADC中，　 ∠ADB＝∠ADC， ∠B＝∠C， AD＝AD，∴△ADB≌△ADC，∴AB＝AC．
思考：通过这题的证明你发现了什么结论？
定理 有两个角相等的三角形是等腰三角形.(简称“等角对等边”)．
符号语言∵∠B＝∠C∴AB＝AC (等角对等边)
思考： “等边对等角”与“等角对等边” 是否一样？它们的主要区别在哪里？
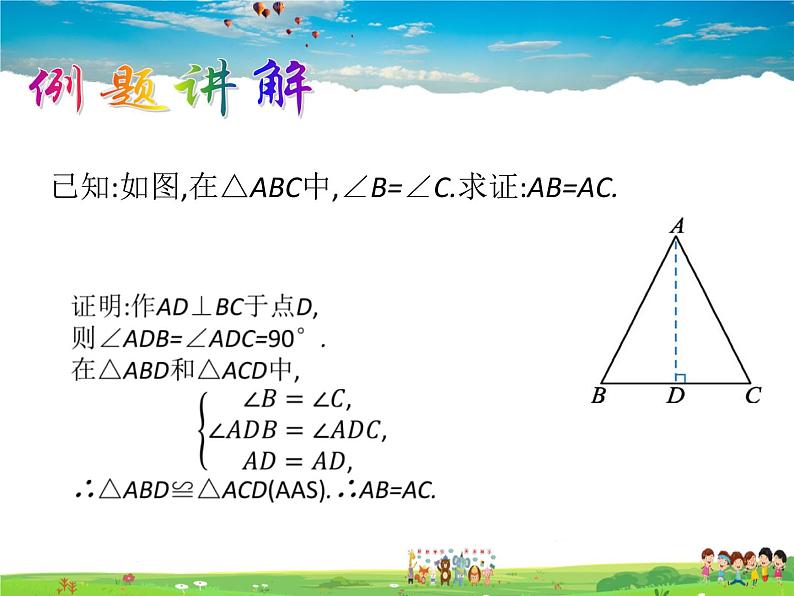
已知:如图,在△ABC中,∠B=∠C.求证:AB=AC.
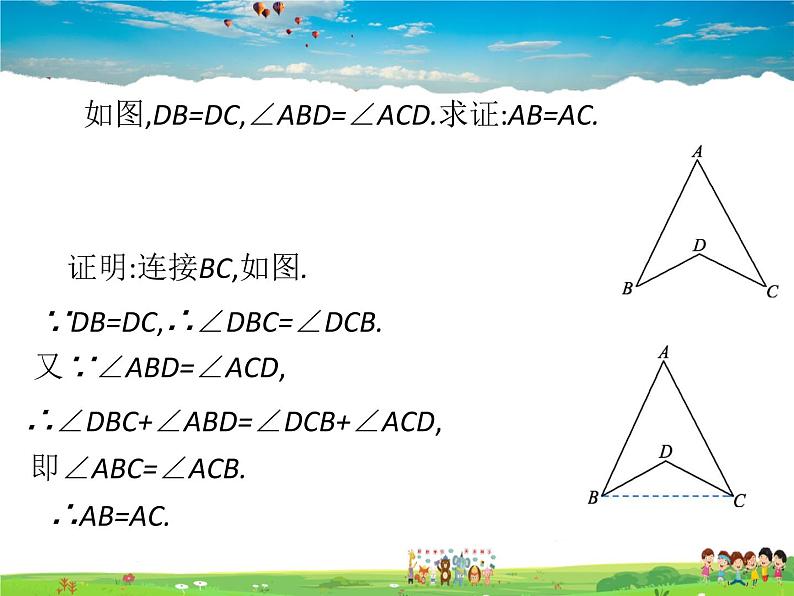
如图,DB=DC,∠ABD=∠ACD.求证:AB=AC.
证明:连接BC,如图.
∵DB=DC,∴∠DBC=∠DCB.
又∵∠ABD=∠ACD,
∴∠DBC+∠ABD=∠DCB+∠ACD,
即∠ABC=∠ACB.
思考1：什么是等边三角形？它与等腰三角形有什么区别与联系？
思考2：等边三角形的性质有哪些？
等边三角形的概念及性质（1）三边相等的三角形叫作等边三角形或正三角形．（2）等边三角形是轴对称图形，并且有3条对称轴．（3）等边三角形的各角都等于60°．
如图所示,在等边△ABC中,D是AC边的中点,延长BC到点E,使CE=CD,连接DE,试判断△BDE的形状,并说明理由.
思考3：一个三角形满足什么条件就是等边三角形？为什么？
等边三角形的判定（1）三个角都相等的三角形是等边三角形．（2）有一个角是60°的等腰三角形是等边三角形 ．
如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,AN交CM于点E,BM交CN于点F.求证:(1)CE=CF;(2)EF∥AB.
(2)由(1)知,CE=CF.∴△ECF为等腰三角形.又∵∠MCN=60°,∴△ECF为等边三角形.∴∠EFC=∠FCB=60°.∴EF∥AB.
图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE.求证:BD=2CE.
如图,在△AB中,AB=AC,∠A=60°,BD⊥AC于D,E为BC的中点,DF⊥DE交BC的延长线于点F.求证:E、C两点是线段BF的三等分点.
如图所示,在△ABC中,AB=AC,AD平分∠BAC,E是AC延长线上的一点,且CE=CD,AD=DE.(1)求证:△ABC是等边三角形;(2)如果把AD 改成△ABC的中线或高线,其余条件不变,请判断(1)中的结论是否依然成立?(只要求写出结论,不要求证明)
解:(1)证明:∵CD=CE,∴∠E=∠CDE,∴∠ACB=2∠E.∵AD=DE,∴∠E=∠DAC.∵AD平分∠BAC,∴∠BAC=2∠DAC=2∠E,∴∠ACB=∠BAC,∴BA=BC.∵AB=AC,∴AB=BC=AC,∴△ABC是等边三角形.(2)解:当AD为△ABC的中线或高线时,结论依然成立.