初中数学北师大版九年级下册5 二次函数与一元二次方程一等奖课件ppt

这是一份初中数学北师大版九年级下册5 二次函数与一元二次方程一等奖课件ppt，共23页。PPT课件主要包含了跟踪练习，1＜x＜12，课堂练习，综合拓展，①③④等内容，欢迎下载使用。
1.经历探索二次函数图象与一元二次方程近似根的过程, 体会数形结合 思想研究问题的重要意义2.会利用二次函数的图象求一元二次方程的近似根.(重点)3. 通过对综合问题的学习和训练提升学生综合分析、解决问题的能力（难点）
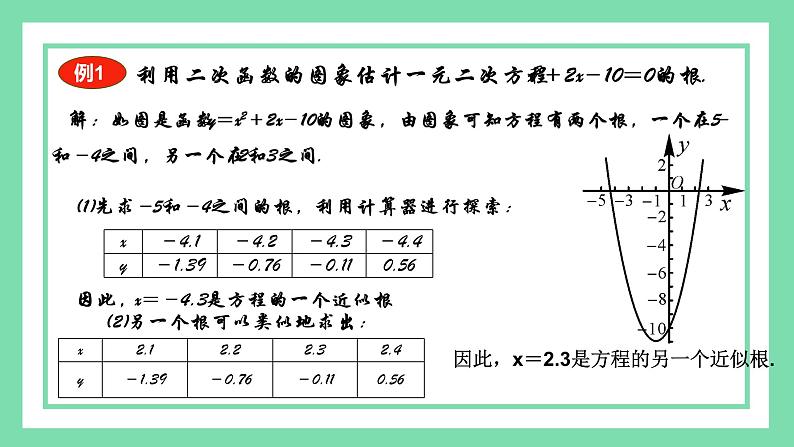
　利用二次函数的图象估计一元二次方程x2＋2x－10＝0的根.
解：如图是函数y＝x2＋2x－10的图象，由图象可知方程有两个根，一个在－5和－4之间，另一个在2和3之间.
(1)先求－5和－4之间的根，利用计算器进行探索：
因此，x＝－4.3是方程的一个近似根.
(2)另一个根可以类似地求出：
　　因此，x＝2.3是方程的另一个近似根.
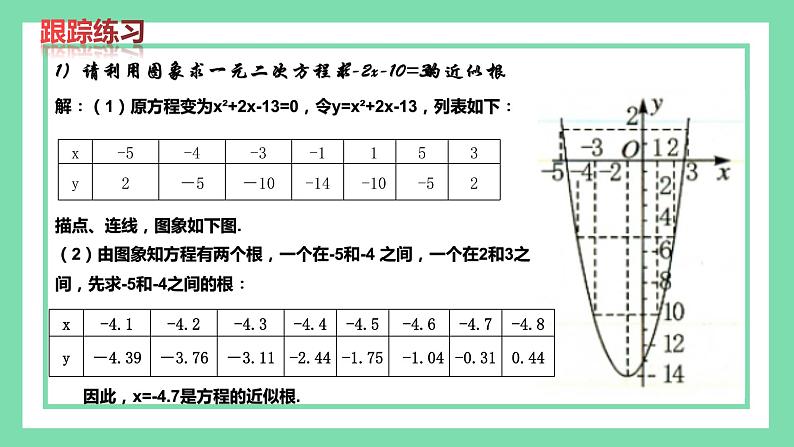
1）请利用图象求一元二次方程求x2-2x-10=3的近似根.
解∶（1）原方程变为x²+2x-13=0，令y=x²+2x-13，列表如下∶描点、连线，图象如下图.（2）由图象知方程有两个根，一个在-5和-4 之间，一个在2和3之间，先求-5和-4之间的根∶
因此，x=-4.7是方程的近似根.
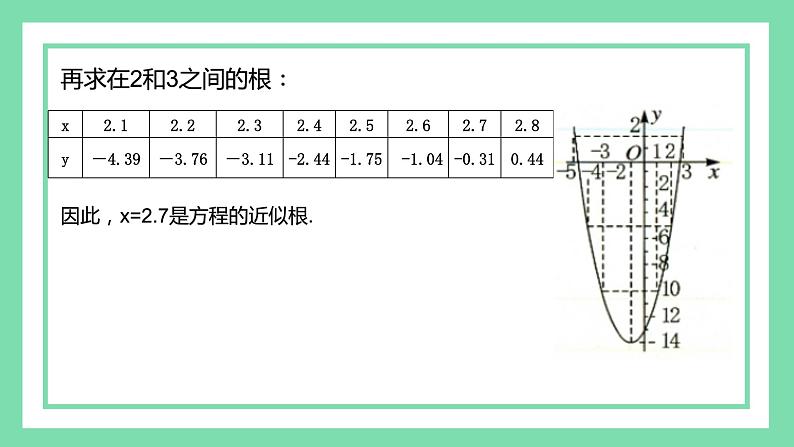
再求在2和3之间的根∶
因此，x=2.7是方程的近似根.
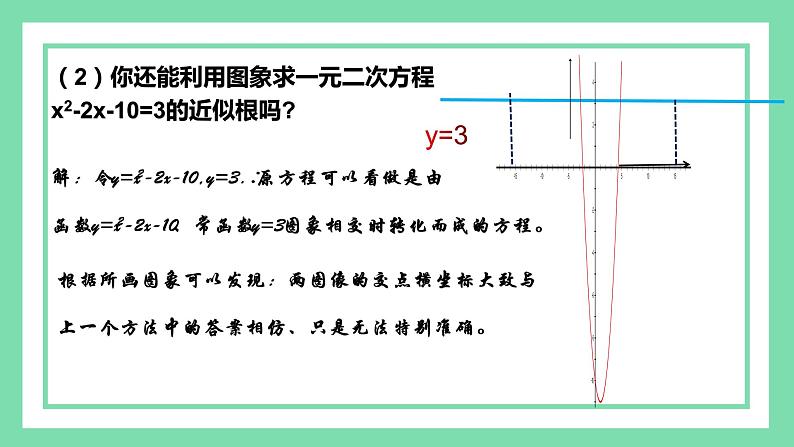
（2）你还能利用图象求一元二次方程x2-2x-10=3的近似根吗?
解：令y=x2-2x-10,y=3.∴原方程可以看做是由函数y=x2-2x-10、常函数y=3图象相交时转化而成的方程。
根据所画图象可以发现：两图像的交点横坐标大致与上一个方法中的答案相仿、只是无法特别准确。
(1)将方程化为一般形式ax2＋bx＋c＝0；(2)画出二次函数y＝ax2＋bx＋c的图象；(3)根据抛物线y＝ax2＋bx＋c与x轴的交点的横坐标确定方程的根的大致范围；(4)列表格，在第(3)步中确定的两个数之间取值，进行估算，通常只精确到十分位即可；(5)确定近似值时，取y的绝对值最小时，对应x的值为根.
用图象法估计一元二次方程ax2＋bx＋c(a≠0)根的近似值的一般步骤：
1、下表是满足二次函数y＝ax2＋bx＋c的五组数据，x1是方程ax2＋bx＋c＝0的一个解，则下列选项中正确的是( )
A.1.6＜x1＜1.8 　　 B.1.8＜x1＜＜x1＜2.2 　　 D.2.2＜x1＜2.4
2.二次函数 y＝x2＋px＋q 部分对应值可列表如下：
则一元二次方程x2＋px＋q＝0正根的范围是 .
1.根据抛物线y=x²＋3x-1与x轴的交点的坐标，可以求出下列方程中哪个方程的近似解（ ）A.x2+3x-1=0 B.x2+3x+1=0 C.3x2+x-1=0 D.x2-3x+1=0
2.小明利用二次函数的图象估计方程 x²-2x-2=0 的近似解，如表是小明探究过程中的一些计算数据.根据表中数据可知，方程 x²-2x-2=0必有一个实数根在（ ）A．1.5和2之间 B.2和2.5之间 C.2.5和3之间 D.3和3.5之间
3.下表是一组二次函数 y=x²＋3x一5的自变量x与函数值y的对应值∶那么方程 x²+3x一5=0的一个近似根是（ ）A.1 B.1.1 C.1.2 D.13
利用二次函数y=2x2.与一次函数y=x+2的图象，求一元二次方程2x²=x+2的近似根.
解：如图 两个函数图象的交点横坐标大约是x1≈0.8 x2≈1.3
∴由两个函数组成的新方程的公共解就是 x1≈0.8 x2≈1.3
1、如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（-1，0）；⑤当1＜x＜4时，有y2＜y1，其中正确的是（　　）A①②③ B①③④ C①③⑤ D②④⑤
解析：本题依据“对称轴为x=1，开口方向，对称轴的位置，与y轴的交点位置”四条信息可以判断出①√②×；③中的方程是由函数y=ax2+bx+c与y=3组成。其方程根取决于对应函数的图象交点，由图可以发现，③√又∵对称轴为x=1,并且图象与x轴的一个交点横坐标为4，∴可以推断出④×;最后⑤当1＜x＜4时，有y2＜y1√
2、（湖北.孝感）如图是抛物线y=ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：①a﹣b+c＞0；②3a+b=0；③b2=4a（c﹣n）；④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根．其中正确结论的是 。
解：抛物线与x轴的一个交点在点（3，0）和（4，0）之间，而抛物线的对称轴为直线x=1，∴抛物线与 x轴的另一个交点在点（-2，0）和（-1，0）之间. ..当x= -1时，y>0，即a-b+c>0，所以①正确;∵ 抛物线的对称轴为直线 x= -1，即b=-2a，3a+b=3a-2a=a，所以②错误;由顶点纵坐标公式可得b²=4ac-4an =4a（c-n），所以③正确;∵ 抛物线与直线y=n 有一个公共点，.抛物线与直线y=n-1有2个公共点，.一元二次方程 ax²+bx +c=n-1有两个不相等的实数根，所以④正确.故选;C.
3、如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a(x+m)2+n的顶点在线段AB上，与x轴交于C，D两点（C在D的左侧），点C的横坐标最小值为﹣3，则点D的横坐标的最大值为 ．
解析∶当点C的横坐标为—3时，抛物线顶点为A（1，4），对称轴为直线 x=1，此时D点的横坐标为5，则 CD=8.当抛物线顶点为 B（4，4）时，抛物线的对称轴为直线x=4，且CD=8，故C（0，0），D（8，0）.由于此时D点横坐标最大，所以点 D的横坐标的最大值为8.
4、 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＞m（am+b）（m≠1的实数）．其中正确的结论有（　　）A．2个B．3个C．4个D．5个
5、二次函数y = ax²+ bx +c(a≠0）的图象如图所示，若lax²+ bx+cl= k有两个不相等的实数根，则 k的取值范围是( )A.k-3 C.k3
D 【解析】 当ax²+bx+c≥0时，y=lax²+bx+cl=ax²+bx+c，此时y=lax²+bx +cl的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象（包括与x轴的交点）;当αx²+bx+c3.故选 D.
6、如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b＜0；②﹣1≤a≤- ；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根．其中结论正确的个数为（　　）
A．1个B．2个C．3个D．4个