2021学年12.3 互逆命题课堂教学ppt课件

这是一份2021学年12.3 互逆命题课堂教学ppt课件，共16页。PPT课件主要包含了问题情境1，试一试，命题的证明等内容，欢迎下载使用。
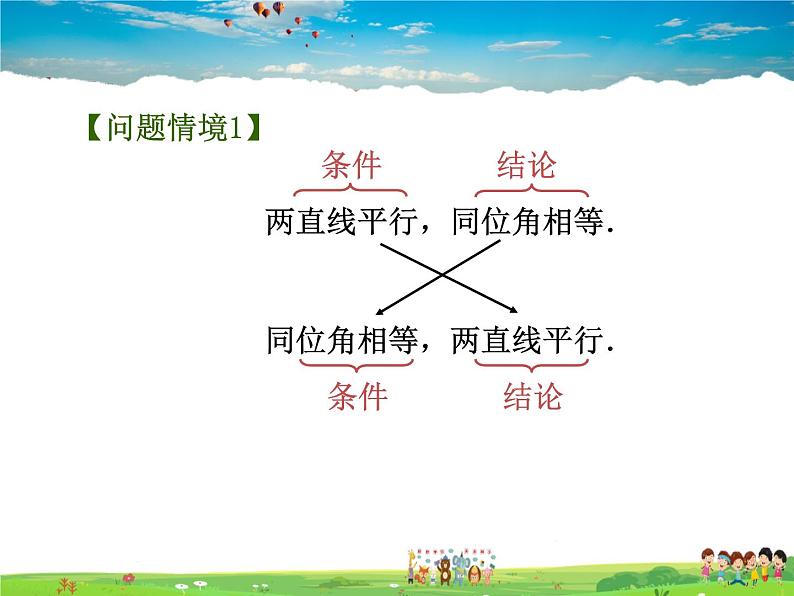
两直线平行，同位角相等．
同位角相等，两直线平行．
如果 a＋b＞0 ，那么 a＞0，b＞0
如果 a ＞0，b ＞0 ，那么 a＋b＞0
两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题. 其中一个命题是另一个命题的逆命题.
　　1．下列各组命题是否是互逆命题：　　（1）“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”；　　（2）“等于同一个角的两个角相等”与“如果两个角都等于同一个角，那么这两个角相等”；　　（3）“对顶角相等”与“如果两个角相等，那么这两个角是对顶角”；　　（4）“同位角相等，两直线平行”与“同位角不相等，两直线不平行” ．
2 ．说出下列命题的逆命题，并与同学交流．（1）如果a2＝b2，那么a＝b；（2）如果两个角是对顶角，那么它们的平分线组成一个平角；（3）末位数字是5的数，能被5整除；（4）锐角与钝角互为补角.
逆命题：如果a＝b，那么a2＝b2 .
逆命题：如果两个角的平分线组成一个平角，那么这两个角是对顶角.
逆命题：能被5整除的数的末位数字是5．
逆命题：互为补角的两个角一个是锐角一个是钝角．
在你已经学习过的命题中，举出两个命题，它们不仅是逆命题，而且都是真命题．
如图：　（1）如果AD∥EF，那么可以得到什么结论？　（2）如果∠EFC＋∠C＝180°，那么可以得到什么结论呢？　（3）证明AD∥EF，需要什么条件？证明EF∥BC 呢？　（4）证明AD∥EF∥BC，需要什么条件？
图形特殊的“位置关系”常常决定了图形具有特殊的“数量关系”； 反过来，图形特殊的“数量关系”常常决定了图形具有特殊的“位置关系”．
例1　证明：平行于同一条直线的两条直线平行．
已知：如图，直线a、b、c 中，b∥a， c∥a．求证：b∥c ．
证明：作直线a、b、c的截线d．　　　∵b∥a (已知)，　　　∴∠2＝∠1 (两直线平行，同位角相等)，　　　　　　　　∵c∥a (已知)，　　　∴∠3＝∠1 (两直线平行，同位角相等)，　　　　　　　∴∠2＝∠3 (等量代换)，　　　∴b∥c (同位角相等，两直线平行)．
例2　证明：直角三角形的两个锐角互余．
已知：如图，在△ABC 中，∠C＝90°，求证：∠A＋∠B＝90°．
证明：在△ABC 中， ∠A＋∠B＋∠C ＝180° （三角形三个内角的和等于180°）， ∴∠A ＋∠B ＝ 180°－ ∠C（等式性质)， 　　 ∵ ∠C ＝ 90°(已知)， ∴∠A ＋∠B ＝ 180°－ 90°（等量代换)， ∴ ∠A ＋∠B ＝ 90°．
说出命题“直角三角形的两个锐角互余”的逆命题．这个命题是真命题吗？为什么？
构造一个命题的逆命题，并证明这个命题是真命题，我们就能探索并获得一些新的数学结论．
这是一种逆向思考研究问题的方法．
【练习】1． (1)如图，AB∥CD，AB、DE 相交于点G，∠B＝∠D． 在下列括号内填写推理的依据：∵AB∥CD (已知)，∴∠EGA ＝∠D ( )．又∵∠B ＝∠D (已知)，∴∠EGA ＝∠B( )，∴DE∥BF ( )． (2)上述推理中，应用了哪两个互逆的真命题？
　　2.（1）已知：如图，在直角三角形ABC 中∠ACB ＝ 90°，D 是AB 上一点，且∠ACD ＝∠B ．求证：CD⊥AB．（2）你在（1）的证明过程中应用了哪两个互逆的真命题？
【小结】 通过今天的学习，你有哪些收获与体会，说出来和同学们分享．