初中数学湘教版七年级上册4.2 线段、射线、直线课前预习ppt课件

这是一份初中数学湘教版七年级上册4.2 线段、射线、直线课前预习ppt课件，共30页。PPT课件主要包含了学习目标，导入新课，情境引入，议一议，讲授新课，比较两条线段的长短，1度量法，2叠合法，叠合法结论，解作图步骤如下等内容，欢迎下载使用。
1. 会用尺规画一条线段等于已知线段，会比较两 条线段的长短. (重点)2. 理解线段等分点的意义.3. 能够运用线段的和、差、倍、分关系求线段的 长度. (重点、难点)4. 体会文字语言、符号语言和图形语言的相互转化.5. 了解两点间距离的意义，理解“两点之间，线段 最短”的线段性质，并学会运用. (难点)
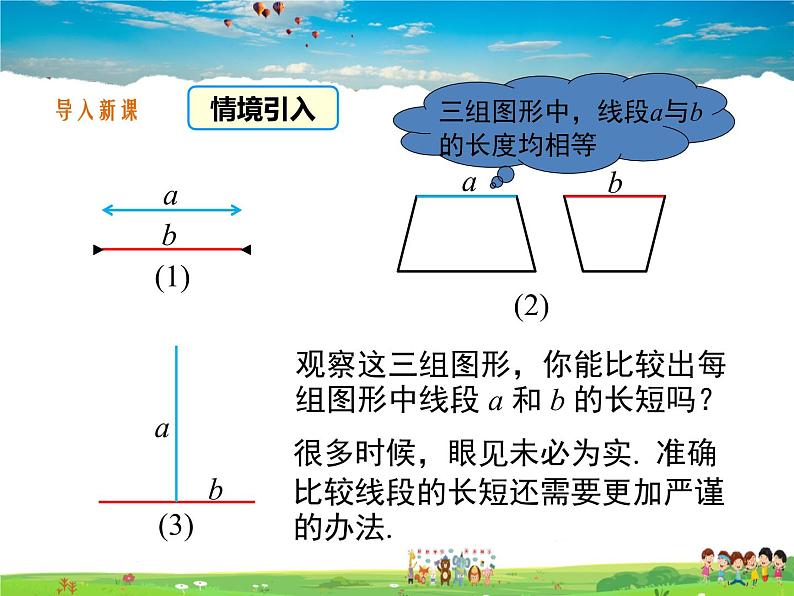
观察这三组图形，你能比较出每组图形中线段 a 和 b 的长短吗？
很多时候，眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
下图中哪棵树高？哪支铅笔长？窗框相邻的两条边哪条边长？你是怎么比较的？与同伴进行交流.
思考：怎样比较两条线段的长短?？
将其中一条线段“移动”，使其一端点与另一线段的一端点重合，两线段的另一端点均在同一射线上.
用刻度尺量出它们的长度，再进行比较.
1. 若点 A 与点 C 重合，点 B 落 在C，D之间，那么 AB CD.
2. 若点 A 与点 C 重合，点 B 与 点 D ，那么 AB = CD.
3. 若点 A 与点 C 重合，点 B 落 在 CD 的延长线上，那么 AB CD.
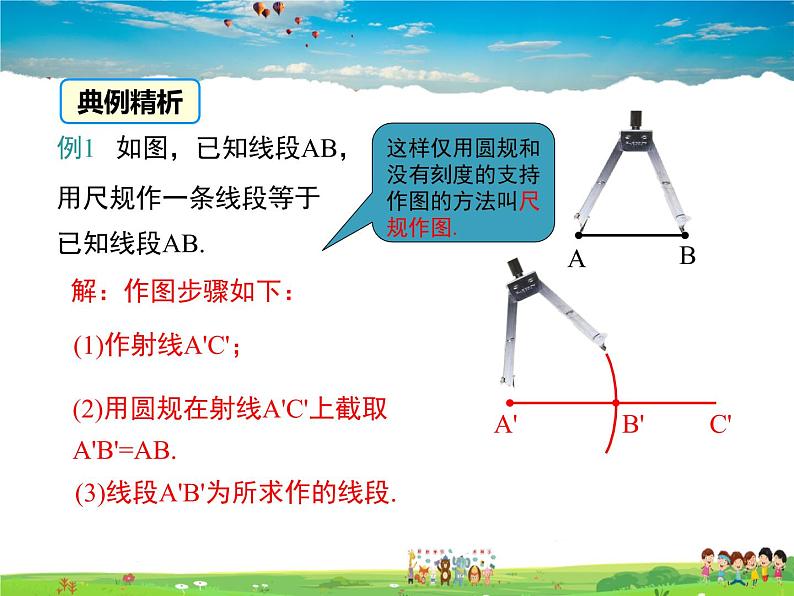
例1 如图，已知线段AB，用尺规作一条线段等于已知线段AB.
(1)作射线A'C'；
(2)用圆规在射线A'C'上截取A'B'=AB.
(3)线段A'B'为所求作的线段.
A' C'
这样仅用圆规和没有刻度的支持作图的方法叫尺规作图.
在直线上画出线段 AB=a ，再在 AB 的延长线上画线段 BC=b，线段 AC 就是 与 的和，记作 AC= . 如果在 AB 上画线段 BD=b，那么线段 AD 就是 与 的差，记作AD= .
如图，点B，C在线段 AD 上则AB+BC=____； AD－CD=___；BC＝ ___ －___= ___ － ___.
在一张纸上画一条线段，折叠纸片，使线段的端点重合，折痕与线段的交点处于线段的什么位置？
如图，点 M 把线段 AB 分成相等的两条线段AM 与 BM，点 M 叫做线段 AB 的中点. 类似地，还有线段的三等分点、四等分点等.
M 是线段 AB 的中点
点 M , N 是线段 AB 的三等分点：
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
例2　如图，在直线上有A，B，C三点，AB＝4 cm，BC＝3 cm，如果O是线段AC的中点，求线段OB的长度.
解：因为AB＝4 cm，BC＝3 cm， 所以AC＝AB＋ BC＝7 cm.
因为点O是线段AC的中点， 所以OC＝ AC＝3.5 cm.
所以OB＝OC－BC＝3.5－3＝0.5(cm).
(1)逐段计算：求线段的长度，主要围绕线段的和、差、倍、分关系展开．若每一条线段的长度均已确定，所求问题可迎刃而解．
计算线段长度的一般方法：
(2)整体转化：巧妙转化是解题关键．首先将线段转化为两条线段的和，然后再通过线段的中点的等量关系进行替换，将未知线段转化为已知线段．
变式：如果线段AB＝6，点C在直线AB上，BC＝4，D是AC的中点，那么A、D两点间的距离是（　　）A.5 B.2.5 C.5或2.5 D.5或1
方法总结：解答本题关键是正确画图，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解.
例3 如图，B、C两点把线段AD分成2∶3∶4的三部分，点E是线段AD的中点，EC＝2cm，求：（1）AD的长；（2）AB∶BE.
解：（1）设AB＝2x，则BC＝3x，CD＝4x， 由线段的和差，得AD＝AB＋BC＋CD＝9x.由E为AD的中点，得ED＝ AD＝ x.由线段的和差得，CE＝DE－CD＝ x－4x＝ ＝2.解得x＝4.∴AD＝9x＝36（cm）.
解：AB＝2x＝8，BC＝3x＝12.由线段的和差，得BE＝BC－CE＝12－2＝10（cm）.∴ AB∶BE＝8∶10＝4∶5.
方法总结：在遇到线段之间比的问题时，往往设出未知数，列方程解答.
如图,从A地到B地有四条道路，除它们外能否再修一条从A地到B地的最短道路？如果能，请你在图上画出最短路线.
发现：两点之间的所有连线中，线段最短
2.我们把两点之间线段的长度，叫做这两点之间的距离.
1.上述发现可以总结为：
1. 如图，这是 A，B 两地之间的公路，在公路工程 改造计划时，为使 A，B 两地行程最短，应如何 设计线路？请在图中画出，并说明理由.
2. 把原来弯曲的河道改直，A，B 两地间的河道长 度有什么变化？
A，B 两地间的河道长度变短.
[解析] 在MN上任选一点P，它到A，B的距离即线段PA与PB的长，结合两点之间线段最短可求．
解：连接AB，交MN于点P，则这个货站应建在点P处.
(1)两点之间的距离的概念描述的是数量，而不是图形，指的是连接两点的线段的长度，而不是线段本身． (2)在解决选择位置、求最短距离等问题时，通常转化为“两点之间线段最短”．
1.用圆规截取的方法比较图中下列两组线段的大小：
（1） AC 和AB； （2） BC 和AB.
（1） AC < AB
（2） BC < AB
2.如图，AB+BC AC，AC+BC AB， AB+AC BC（填“>”“b)作一条线段使它等于a-b.
解：作图步骤如下：
(1) 作射线AF；
(2) 在射线AF上截取AC=a;
(3) 在线段AC截取AB=b.
则线段BC就是所要求作的线段.
6.已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6，求CM和AD的长．
AD=10x=20 ．
解：设AB=2x，BC=5x，CD=3x,
所以AD=AB+BC+CD=10x.
所以AM=MD=5x，
所以BM=AM-AB=3x.
即3x=6，所以x=2.
故CM=MD-CD=2x=4，