江苏省扬州市2021-2022学年高三上学期期中调研考试数学试题(解析版)

这是一份江苏省扬州市2021-2022学年高三上学期期中调研考试数学试题(解析版)，共14页。

一、单项选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合要求)
1．若集合eq A＝{x|x\s\up6(2)－3＞0}，B＝{0，1，2，3，4}，则A∩B中元素的个数为( )．
A．2 B．3 C．4 D．5
2．已知幂函数eq f(x)＝x\s\up6(α)的图象经过点(4，2)，则f(9)的值为( )．
A． －3 B． 3 C．－9 D．9
3．已知a＝2022EQ \S\UP8(\F(1,2021))，b＝lg20222021，c＝lg2022eq \f(1,2021)，则a，b，c的大小关系为( )．
A．a＞b＞c B．b＞a＞c C．c＞a＞b D．a＞c＞b
4．已知a，b∈R，且a＞b，则下列选项中正确的是角的( )．
A．eq \f(1,a)＜eq \f(1,b) B．eq a\s\up6(2)＞b\s\up6(2) C．|a|＞|b| D．eq 2\s\up6(a)＞2\s\up6(b)
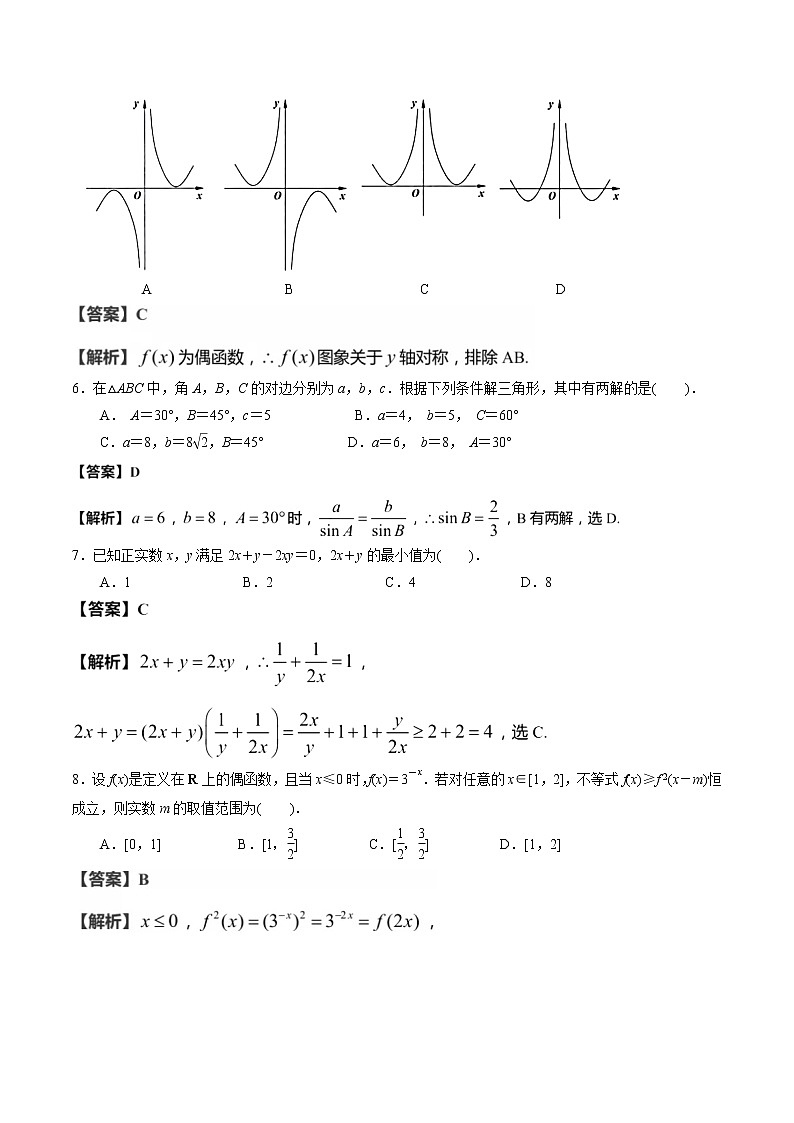
5．函数eq y＝\f(1,x\s\up6(2))＋csx＋1的部分图大致为( )．
A B C D
6．在△ABC中，角A，B，C的对边分别为a，b，c．根据下列条件解三角形，其中有两解的是( )．
A． A＝30°，B＝45°，c＝5 B．a＝4， b＝5， C＝60°
C．a＝8，b＝eq 8\r(,2)，B＝45° D．a＝6， b＝8， A＝30°
7．已知正实数x，y满足2x＋y－2xy＝0，2x＋y的最小值为( )．
A．1 B．2 C．4 D．8
8．设f(x)是定义在R上的偶函数，且当x≤0时，eq f(x)＝3\s\up6(－x)．若对任意的x∈[1，2]，不等式f(x)≥f 2(x－m)恒成立，则实数m的取值范围为( )．
A．[0，1] B．eq [1，\f(3,2)] C．eq [\f(1,2)，\f(3,2)] D．[1，2]
二、多项选择题(本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分)
9．已知α、β表示不同的平面，m、n表示不同的直线，则下列命题中正确的有( )．
A．若m//n，nα，则m//α B．若m//α，mβ，α∩β＝n，则m//n
C．若m⊥β，mα，则α⊥β D．若m⊥α，n⊥α，则m//n
10．已知函数eq f(x)＝sin(2x－\f(π,3))，则下列结论中正确的有( )．
A．f(x)的图象的对称中心为eq (\f(kπ,2)＋\f(π,6)，0)(k∈Z
B．f(x)的图象可由y＝sin2x的图象向右平移eq \f(π,3)个单位得到
C．f(x)在eq x∈[－\f(π,6)，\f(π,3)]上的值域为eq [－\f(\r(,3),2)，\f(\r(,3),2)]
D．方程f(x)＝1在x∈[0，π]上的根为eq x＝\f(5π,12)
11．中国传统文化中很多内容体现了数学的“对称美”．如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分体现了相互转化、对称统一的形式美、和谐美．在平面直角坐标系中，如果一个函数的图象能够将某个圆的周长和面积同时平分，那么称这个函数为这个圆的“优美函数”．则下列说法中正确的有( )．
A．对于一个半径为1的圆，其“优美函数”仅有1个
B．函数eq f(x)＝x\s\up6(3)－3x可以是某个圆的“优美函数”
C．若函数y＝f(x)是“优美函数”，则函数y＝f(x)的图象一定是中心对称图形
D．函数eq y＝2cs(\f(3π,2)－x)可以同时是无数个圆的“优美函数”
12．已知函数eq f(x)＝\f(x,1＋x\s\up6(2))，则下列说法中正确的有( )．
A．函数f(x)的值域为eq [－\f(1,2)，\f(1,2)]
B．当eq x∈(0，\f(π,2))时，y＝f(x)与y＝tanx的图象有交点
C．函数eq g(x)＝\f(x\s\up6(3)－3x,x\s\up6(4)－5x\s\up6(2)＋9)的最大值为eq \f(1,2)
D．当x≥0时，eq f(x)≤e\s\up6(x)－1恒成立
三、填空题(本大题共4小题，每小题5分，共20分)
13．若函数f(x)＝x＋lnx在x＝1处的切线与直线y＝kx平行，则实数k＝ ．
14．用几种不同的乐器同时弹奏某一首乐曲时，我们有时能听到比用单一乐器弹奏时更美妙的声音，这实际上是几种声波合成后改变了单一声波的波形．假设某美妙声波的传播曲线可用函数eq v＝\r(,2)sin(2x＋\f(π,4))－2sin2x来描述，则该声波函数的最小正周期为 ．
15．在三棱锥O－ABC中，AB＝2，eq AC＝2\r(,3)，BC＝4，且侧棱长均为eq 2\r(,5)，则该三棱锥外接球的表面积为 ．
16．若函数eq f(x)＝ae\s\up6(x)－\f(1,2)x\s\up6(2)＋3(a∈R)有两个不同的极值点eq x\s\d(1)和eq x\s\d(2)，则a的取值范围为 ；若eq x\s\d(1)＜eq x\s\d(2)≤2eq x\s\d(1)，则a的最小值为 ．
四、解答题(本大题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤)
17．(本小题满分10分)
已知集合eq A＝{x|x\s\up6(2)－x≤0}，记函数eq f(x)＝\r(,1－ax\s\up6(2))(a＞0)的定义域为集合B．
(1)当a＝1时，求A∪B；
(2)若“x∈A”是“x∈B”的充分不必要条件，求实数a的取值范围．
【解析】
18．(本小题满分12分)
已知函数f(x)＝Asin(ωx＋φ)(eq A＞0，ω＞0，|φ|＜\f(π,2))的部分图象如图所示．
(1)求函数f(x)的解析式，并求出该函数的单调递增区间；
(2)若eq α∈(0，\f(π,2))，且eq f(\f(α,2)＋\f(π,6))＝\f(6,5)，求eq f(\f(α,2)－\f(π,6))的值．
【解析】
19．(本小题满分12分)
如图，已知梯形ABCD与正方形ABEF所在平面垂直，AD∥BC，AD＝AB＝eq \f(1,2)BC＝1，BD＝EQ \R(,2)，且eq \\ac(\S\UP7(→),EM)＝2\\ac(\S\UP7(→),MC)．
(1)证明：BE⊥CD；
(2)求二面角M－BD－C的余弦值．
【解析】
z
y
x
20．(本小题满分12分)
在①(2b－c)csA＝acsC，②(sinA＋sinB)(a－b)＝c(sinC－sinB)，
③eq tanA＋tanB＋tanC＝\r(,3)tanBtanC这三个条件中任选一个，补充在下面的横线上，并加以解答．
已知△ABC的内角A，B，C所对的边分别是a，b，c，若 ．
(1)求A；
(2)若点M在线段AC上，∠ABM＝∠CBM，eq BM＝\f(5,3)\r(,7)，且eq csB＝\f(1,7)，求c．
【解析】
21．(本小题满分12分)
某种疾病可分为Ⅰ、II两种类型．为了解该疾病类型与性别是否有关，在某地区随机抽取了男女患者各200名，每位患者患Ⅰ型或II型病中的一种，得到下面的列联表：
(1)根据列联表，判断是否有99%的把握认为所患疾病类型与性别有关．
(2)某药品公司欲研发此疾病的治疗药物，现有两种试验方案，每种方案至多安排2个接种周期，且该药物每次接种后出现抗体的概率为p(0＜p＜1)，每人每次接种的费用为m元(m为大于零的常数)．
方案一：每个周期必须接种3次，若在第一个周期内3次出现抗体，则终止试验；否则进入第二个接种周期．
方案二：每个周期至多接种3次，若第一个周期前两次接种后均出现抗体，则终止本周期的接种，进入第二个接种周期，否则需依次接种完3次，再进入第二个接种周期；若第二个接种周期第1次接种后出现抗体，且连同第一个接种周期共3次出现抗体，则终止试验，否则需依次接种完3次．
假设每次接种后出现抗体与否相互独立．用随机变量X和Y分别表示按方案－－和方案二进行一次试验的费用．
①求E(X)和E(Y)；
②从平均费用的角度考虑，哪种方案较好?
参考公式：χ2＝eq \f(n(ad－bc)\s\up6(2),(a＋b)(c＋d)(a＋c)(b＋d))，其中n＝a＋b＋c＋d．
参考数据：
【解析】
22．(本小题满分12分)
已知函数eq f(x)＝e\s\up6(x)－ax－a，g(x)＝\f(alnx－ax\s\up6(2)＋a－e,x)(a≥0)，其中e是自然对数的底数．
(1)当a＝e时，求f(x)的最小值；
(2)讨论g(x)的零点个数；
(3)若存在x∈(0，＋∞)，使得f(x)≤g(x)成立，求a的取值范围．
【解析】
Ⅰ型病
II型病
男
150
50
女
125
75
P(χ2≥x0)
0.10
0.05
0.025
0.010
0.005
0.001
x0
2.706
3.841
5.024
6.635
7.879
10.828