小学数学北京版四年级下册五 解决问题授课ppt课件

这是一份小学数学北京版四年级下册五 解决问题授课ppt课件，共23页。PPT课件主要包含了学习目标，复习导入，情景导入1，探究新知，画线段图，解决问题，情景导入2，典题精讲，解题思路，易错提醒等内容，欢迎下载使用。

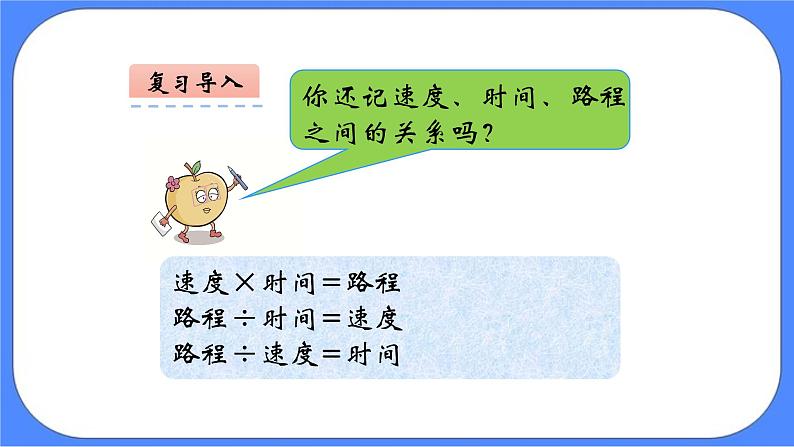
1. 掌握“相遇问题”的特征和解题方法。
2.会利用坐标纸通过画图解答相遇问题。
速度×时间=路程路程÷时间=速度路程÷速度=时间
一列火车从甲地开往乙地， 以每时120千米的速度行驶了20小时，甲、乙两地相多远？
根据路程=速度×时间。
120×20=2400（千米）
答：甲乙两地相距2400千米。
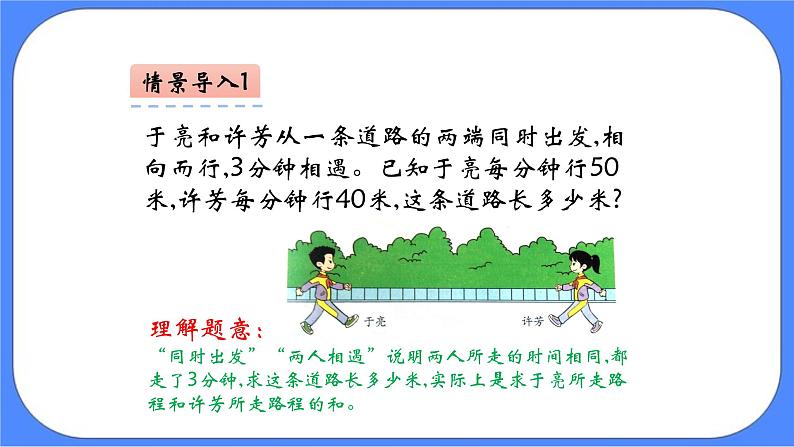
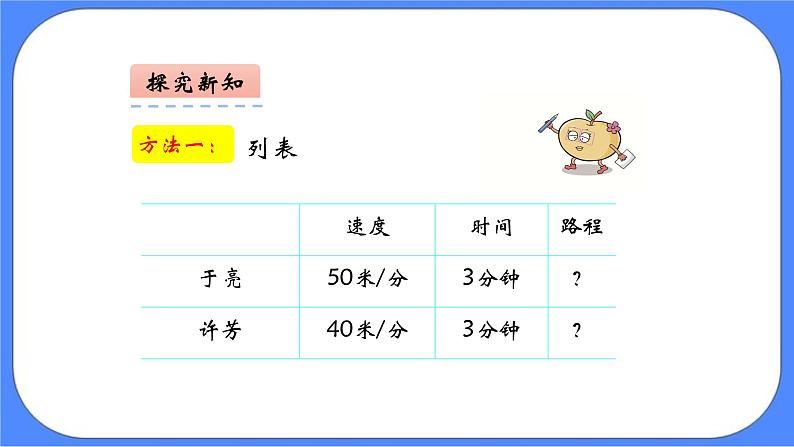
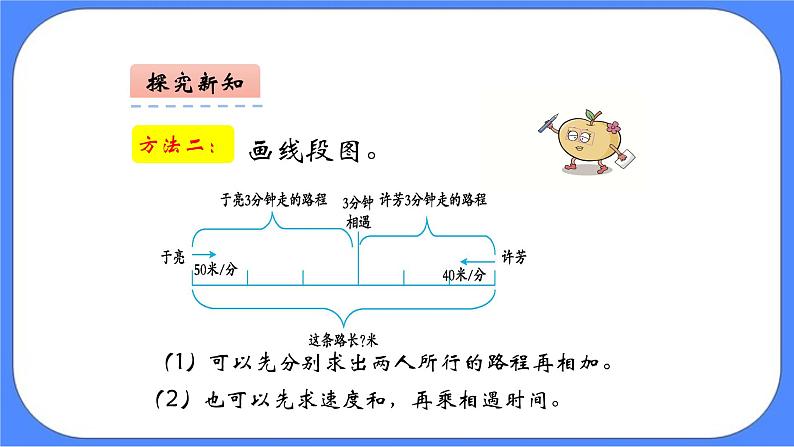
于亮和许芳从一条道路的两端同时出发,相向而行,3分钟相遇。已知于亮每分钟行50米,许芳每分钟行40米,这条道路长多少米?
理解题意：“同时出发”“两人相遇”说明两人所走的时间相同,都走了3分钟,求这条道路长多少米,实际上是求于亮所走路程和许芳所走路程的和。
（1）可以先分别求出两人所行的路程再相加。
（2）也可以先求速度和，再乘相遇时间。
方法一:于亮3分钟走的路程+许芳3分钟走的路程=这条路的长度　50×3+40×3　　=150+120　　=270(米)
方法二:两人1分钟共走的路程×走的时间=这条路的长度　(50+40)×3　　=90×3　　=270(米)
答：这条道路长270米。
方法二较为简单,求总路程可以利用关系式:速度和×相遇时间=总路程。
于亮和许芳从一条长270米的道路两端同时出发,相向而行。已知于亮每分钟行50米,许芳每分钟行40米,经过几分钟两个人相遇?
理解题意：已知于亮和许芳两人所走的总路程和各自的速度,求他们的相遇时间,根据相遇时间=总路程÷速度和。
(1)于亮和许芳同时行了1分钟。画出的线段图如下:
(2)于亮和许芳同时行了2分钟。画出的线段图如下:
(3)于亮和许芳同时行了3分钟。画出的线段图如下:
也就是看270里面有几个（50+40）。
270÷(50+40)=270÷90=3(分)
答:经过3分钟两个人相遇。
总路程÷速度和=相遇时间。
总任务÷速度和=完成时间。
1.甲、乙两组工人要铺设11200米光缆,他们同时从两端铺设,甲组每天铺设840米,乙组每天铺设760米。多少天可以完成任务?
11200÷（840+760）=11200÷1600=7（天）
答：7天可以完成任务。
2.甲、乙两组工人要7天能完成铺设光缆任务,他们同时从两端铺设,甲组每天铺设840米,乙组每天铺设760米。光缆一共有多长?
答：光缆一共有11200米。
总任务=速度和×完成时间。
（840+760）×7=1600×7=11200（米）
错误原因：错误地把两车同时同向而行理解成了相遇问题。
一辆客车和一辆货车同时从甲城开往乙城。已知客车平均每小时行驶89千米,货车平均每小时行驶71千米,4小时后两车相距多少千米?　　错误解答: (89+71)×4 =160×4 =640(千米)答：:4小时后两车相距640千米。
已知两车的速度,可以求出速度差,再乘时间,也可以分别求出两车的行驶路程,再用减法计算。
正确解答:　 (89-71)×4=18×4=72(千米)答：4小时后两车相距72千米。
甲、乙两车同时从A、B两地相向而行，甲车每小时行75千米，乙车每小时行66千米，经过4小时两车在途中相遇。A、B两地公路全长多少千米？
（75+66）×4=141×4=564（千米）
答： A、B两地公路全长564千米。
先求出时间，总路程=速度和×时间
两艘客轮分别从两港同时相对驶出,甲客轮每小时行40千米,乙客轮每小时行36千米,早上8时开出,晚上11时相遇,两港口相距多少千米?
11时-8时=3（小时） （40+36）×3 =76×3 =228（千米）
答： 两港口相距228千米。
根据行程距离=时间×速度和
3.甲车从南京站开往上海站，每小时行80千米，乙车同时从上海站开往南京站，每小时行60千米，2个小时后相遇。甲比乙多行了（ ）千米；甲、乙相遇，甲行了（ ）千米，乙行了（ ）千米；甲乙两站的距离是（ ）千米。
40 160 120 280
甲比乙多走了两个3千米。
3×2÷（20-18）=6÷2=3（小时）
答：全程长114千米。
4.甲、乙两人同时分别从两地骑车相向而行，甲每小时行20千米，乙每小时行18千米。两人相遇时距离中点3千米。问全程长多少米？
（20+18）×3=38×3=114（千米）
行程距离=时间×速度和
答：这条隧道长216千米。
5.两个工程队开凿一条隧道,各从一端同时向中间开凿。第一队每天开凿12米,第二队每天开凿15米,经过8天正好凿通。这条隧道长多少米?
（12+15）×8=27×8=216（千米）
1.含有“同时出发”“相向而行”“同一地点”等特征的行程问题叫相遇问题。
2.在相遇问题中,求总路程有两种方法:一种是先求各自走的路程,再相加;另一种是用速度和×相遇时间=总路程。