2020-2021学年山东省滨州市高一上学期期末数学试题（解析版）

这是一份2020-2021学年山东省滨州市高一上学期期末数学试题（解析版），共18页。试卷主要包含了单选题，多选题，填空题，双空题，解答题等内容，欢迎下载使用。
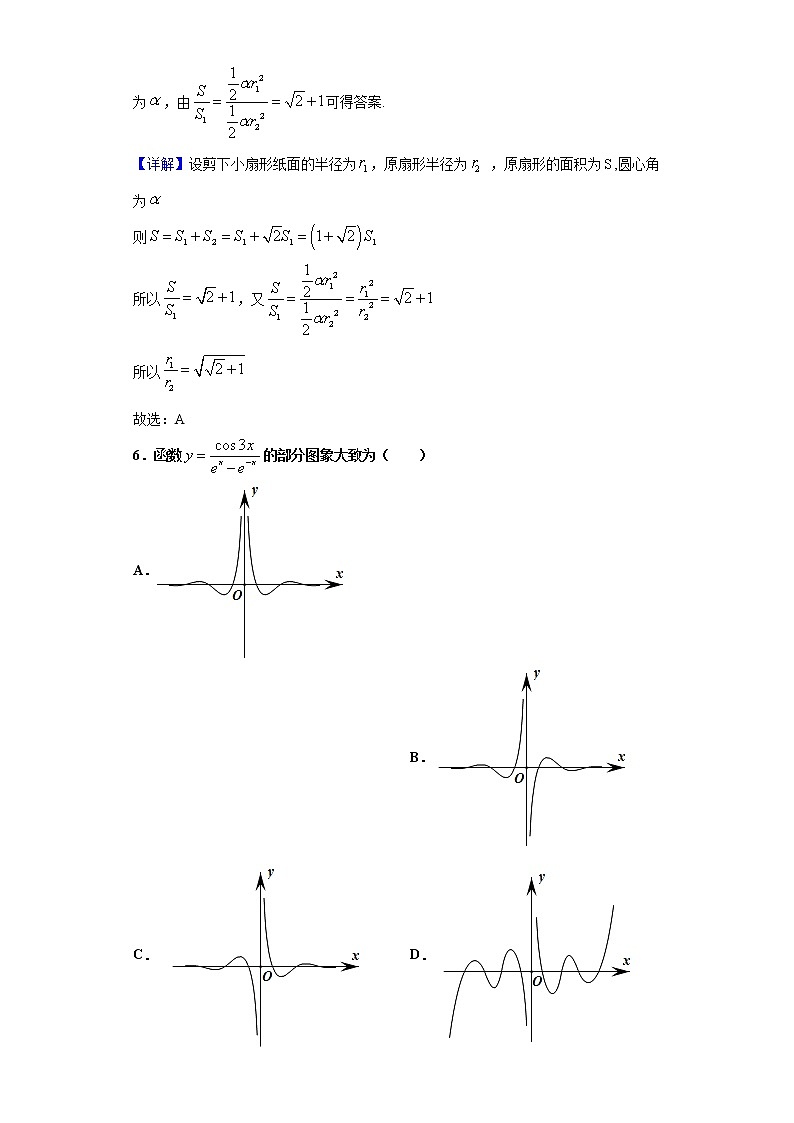
2020-2021学年山东省滨州市高一上学期期末数学试题  一、单选题1．已知命题，则命题的否定是（    ）A． B．C． D．【答案】D【分析】根据命题的否定的定义写出命题的否定，再判断．【详解】命题的否定是．故选：D．2．函数的定义域为（    ）A． B． C． D．【答案】C【分析】根据题意求出使对数和根式有意义的的范围.【详解】由题意可得： 即，解得：，所以原函数的定义域为，故选：C.3．已知，则 （    ）A． B． C． D．【答案】A【分析】分别与0和1比较后可得．【详解】，，，∴，即．故选：A．【点睛】方法点睛：本题考查幂、对数、三角函数值的大小比较．对于具体实数的比较大小，如果能应用函数单调性的应用单调性比较大小，如果不能应用单调性，不同类型的数可以借助中间值如0或1等比较大小后得出结论．4．已知幂函数 在第一象限的图象如图所示，则（    ）A． B． C． D．【答案】B【分析】取，结合图象得出，最后由指数函数的性质得出大小关系.【详解】由图象可知，当时，，则故选：B5．在东方设计中，存在着一个名为“白银比例”的理念，这个比例为，它在东方文化中的重要程度不亚于西方文化中的“黄金分割比例”，传达出一种独特的东方审美观.折扇纸面可看作是从一个扇形纸面中剪下小扇形纸面制作而成（如图）.设制作折扇时剪下小扇形纸面面积为，折扇纸面面积为，当时，扇面较为美观.那么按“白银比例”制作折扇时，原扇形半径与剪下小扇形半径之比为（    ）A． B． C． D．【答案】A【分析】设剪下小扇形纸面的半径为，原扇形半径为 ，原扇形的面积为,圆心角为，由可得答案.【详解】设剪下小扇形纸面的半径为，原扇形半径为 ，原扇形的面积为,圆心角为 则所以，又所以故选：A6．函数的部分图象大致为（    ）A．
 B．C． D．【答案】C【分析】判断函数的奇偶性，函数值的正负，函数值的变化趋势，利用排除法可得结论．【详解】函数定义域是．记，则，是奇函数，排除A；当时，，排除B；当为正数且越来越大时，，越来越大，因此越来越小，排除D．故选：C．【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势；(3)从函数的奇偶性，判断图象的对称性；(4)从函数的特征点，排除不合要求的图象.7．已知函数f（x）＝3x+x，g（x）＝log3x+x，h（x）＝x3+x的零点分别为a，b，c，则a，b，c的大小顺序为（    ）A．a＞b＞c B．b＞c＞a C．c＞a＞b D．b＞a＞c【答案】B【分析】分别求解三个函数的零点满足的关系式,再数形结合利用函数图像的交点比较大小即可.【详解】f（x）＝3x+x＝0,则x＝﹣3x,g（x）＝log3x+x,则x＝﹣log3x,h（x）＝x3+x,则x＝﹣x3,∵函数f（x）,g（x）,h（x）的零点分别为a,b,c,作出函数y＝﹣3x,y＝﹣log3x,y＝﹣x3,y＝x的图象如图,由图可知：b＞c＞a,故选：B.【点睛】本题主要考查了函数零点的运用以及数形结合求解函数值大小的问题,属于中档题.8．已知函数是定义在上的偶函数，当时，，则下列说法正确的是（    ）A．在上为增函数B．的最大值为C．方程有四个不相等的实数根D．当时，【答案】D【分析】求出的解析式，然后判断各选项．其中C选项可能通过函数的交点个数来研究，由与都是偶函数，只要确定在时的交点个数，即可得时的交点个数，结合单调性、函数值易得结论．【详解】时，，D正确；时，，在上，函数递减，A错；同样时，，由于是偶函数，，因此在上，B错；时，，，时，，两函数图象不可能相交，在上，递减，递增，有一个交点，方程有一个解，时，也有一个解，所以方程只有两个解，C错．故选：D．【点睛】思路点睛：本题考查函数的奇偶性，函数的最值，函数的零点等问题．对于偶函数，可以利用对称性，只研究函数在这一部分的性质与结论，利用对称性得出的结论．方程解的个数可以转化为函数图象交点个数，然后利用函数的单调性，函数值的正负等等得出结论，当然也可以作出函数图象，由图象判断． 二、多选题9．在平面直角坐标系中，若角的终边与单位圆交于点 ，将角的终边按逆时针方向旋转后得到角的终边，记角的终边与单位圆的交点为，则下列结论正确的为（    ）A． B． C． D．【答案】ABD【分析】根据三角函数定义求得，由同角间的三角函数关系得、，再由诱导公式得，可判断各选项．【详解】由题意，在第一象限，则，，，，可得ABD正确，C错误．故选：ABD．10．已知，且，则下列不等式恒成立的有（    ）A． B． C． D．【答案】BC【分析】根据不等式的性质判断．错误的可举反例．【详解】，且，则，，，A错误；，则，B正确；，则，C正确；与不能比较大小．如，此时，，D错误．故选：BC．11．下列说法正确的是（    ）A．与角终边相同的角的集合可以表示为B．若为第一象限角，则为第一或第三象限角C．函数是偶函数，则的一个可能值为D．“”是函数的一条对称轴【答案】BD【分析】由判断A，由确定的象限判断B，取得出为奇函数判断C，由判断D.【详解】对于A项，由可知，A错误；对于B项，因为为第一象限角，所以，则，即为第一或第三象限角，B正确；对于C项，当时，为奇函数，C错误；对于D项，由可知，是函数的一条对称轴，D正确；故选：BD【点睛】关键点睛：在判断D选项时，关键是利用对称轴一定过余弦函数的最低点或最高点，从而判断是一条对称轴.12．已知函数若方程有三个实数根，且，则下列结论正确的为（    ）A． B．的取值范围为C．的取值范围为 D．不等式的解集为【答案】ACD【分析】作出函数的图象与直线，它们的交点的横坐标即为，由图可得它们的性质，同时可得出的范围，判断B．由根的性质判断AC，解不等式判断D．【详解】方程的争即为函数的图象与直线的交点的横坐标，作出函数的图象和直线，如图，由图可知：，，，A正确；由于，∴，B错误；由得，∴，∴，C正确；由，时，，，时，，，综上，D正确．故选：ACD． 【点睛】关键点点睛上：本题考查方程根的分布问题，方程的根可以转化函数图象与直线的交点的横坐标，作出函数图象与直线可以直观形象地得出根的性质，同时也得出了函数的性质，由此求解判断各选项．  三、填空题13．已知函数且，且的图象恒过定点，则点的坐标为_________.【答案】【分析】根据对数函数的性质求解．【详解】令，则，，即图象过定点．故答案为：14．已知集合，，若，则实数__________.【答案】【分析】由已知及可得，则或，分别解出得值，再检验集合、满足互异性即可.【详解】由已知及可得，所以或，当即时，此时不满足元素互异性，不符合题意，当即或，若则不满足元素互异性，不符合题意，若则，，满足，符合题意.所以实数，故答案为：.15．函数在区间上的最大值为____________.【答案】【分析】先利用二倍角公式和辅助角公式将的解析式化简，再利用正弦函数的性质即可求最值.【详解】，因为，所以，所以，所以，可得，所以函数在区间上的最大值为，故答案为：. 四、双空题16．已知定义在上的周期函数（在长度不小于它的一个最小正周期的闭区间上）的图象如图所示，则函数的最小正周期为_______，函数的解析式_______. 【答案】2        【分析】根据图象得最小正周期，求出上的函数解析式后可得的解析式．【详解】由图象知最小正周期为2，时，设，由时，，时，设，则，，，所以时，，又它的周期是2，当时，，∴．故答案为：2；【点睛】思路点睛：本题考查函数的周期性，在求周期函数的解析式时，我们只要求得函数在一个周期内的表达式，然后利用周期性扩展到整个实数集上，得出函数的解析式． 五、解答题17．已知集合；（1）若，求实数的取值范围；（2）若，求的值，并从下列所给的三个条件中任选一个，说明它是（1）中的什么条件.（请用“充要条件”“充分不必要条件”“必要不充分条件”“既不充分也不必要条件”回答）①；②；③.【答案】（1）；（2）答案见解析.【分析】（1）解一元二次不等式确定集合，同样解不等式确定集合，根据包含关系得出不等关系，从而求得参数范围；（2）应用对数运算法则计算出，然后不管选哪一个都根据集合包含充分必要条件的关系判断．【详解】解：（1）由，解得.由，解得.因为，所以解得，所以实数的取值范围.（2），.若选①，“”是“”的既不充分也不必要条件.若选②，“”是“”的必要不充分条件:若选③，“”是“”的充分不必要条件.【点睛】结论点睛：本题考查集合的包含关系，本题考查充分不必要条件的判断，一般可根据如下规则判断：命题对应集合，命题对应的集合，则（1）是的充分条件；（2）是的必要条件；（3）是的充分必要条件；（4）是的既不充分又不必要条件集合之间没有包含关系．18．已知函数.（1）若函数在区间上的最大值与最小值之和为，求实数的值；（2）若，求的值.【答案】（1）1；（2）.【分析】（1）在上为增函数，可得， 即可求出实数的值；（2）由，可得，利用对数的运算性质即可求解.【详解】（1）因为在上为增函数，所以，即，解得： (舍去)，或，所以（2）因为，所以，所以，即，所以.19．已知.（1）求的值；（2）求的值.【答案】（1）；（2）.【分析】（1）)先求出，再由两角和的正弦公式计算；（2）根据同角关系求得，二倍角公式得，再由两角和的余弦公式求值．【详解】解：（1）因为，所以，所以，所以（2）因为，由（1）知，所以，所以，所以【点睛】思路点睛：本题考查三角函数的求值．解题关键是选用恰当的公式进行计算．解题时先观察“已知角”和“未知角”的关系，然后确定选用的公式及顺序进行计算求值．在应用平方关系求值时还要注意角的范围，以便确定函数值的正负．20．已知函数为奇函数．（1）求的值；（2）判断函数在上的单调性，并证明．【答案】(1) (2)见解析【分析】（1）根据题意，由奇函数的性质可得，即，解可得的值，即可得答案；（2）根据题意，任取，，且，由作差法分析的符号，由函数单调性的定义分析可得答案．【详解】解：（1）根据题意，为奇函数，则，即，解可得；（2）由（1）的结论，，在上为增函数；证明：任取，，且，则 ，又由，，且，则，，，则有，所以函数在上单调递增．【点睛】本题考查函数奇偶性与单调性的性质以及应用，关键是求出的值，属于基础题．21．已知函数的部分图象如图所示.（1）求函数的解析式；（2）若将函数的图象上所有点的横坐标变为原来的倍，纵坐标不变；再把所得函数图象向左平移个单位长度，得到函数的图象.求函数在上的单调递增区间.【答案】（1）；（2）.【分析】（1）由图可得，，从而再利用周期公式可求出，然后将点的坐标代入可求出，进而可求出函数的解析式；（2）先利用三角函数的图像变化规律求出的解析式，然后令，则，求出的单调递增区间是，然后由，可求出函数的增区间，或先由，得，再结合可求得结果【详解】解：（1）由图可知，，所以，所以.所以.由，所以，所以因为，所以，所以（2）由题设可得，.方法一：令，则.因为的单调递增区间是.且由，得所以函数的单调递增区间是方法二：令解得，因为，所以函数的单调递增区间是22．近来，国内多个城市纷纷加码布局“夜经济”，以满足不同层次的多元消费，并拉动就业、带动创业，进而提升区域经济发展活力.某夜市的一位工艺品售卖者，通过对每天销售情况的调查发现：该工艺品在过去的一个月内（按天计），每件的销售价格 (单位：元)与时间（单位：天）（）的函数关系满足（为常数，且），日销售量（单位：件）与时间的部分数据如下表所示：设该工艺品的日销售收入为（单位：元），且第天的日销售收入为元.（1）求的值；（2）给出以下四种函数模型：①；②；③；④.请你根据上表中的数据，从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系，并求出该函数的解析式；（3）利用问题（2）中的函数，求的最小值.【答案】（1）1；（2）；（3）441.【分析】（1）由可求得；（2）由数据知先增后减，选择②，由对称性求得，再利用其他函数值求出；（3）根据（2）求得的表达式，然后一段利用基本不等式求得最小值，一段利用函数的单调性刘最小值，比较可得结论．【详解】解:（1）因为第天的日销售收入为元，所以，解得.（2）由表中的数据知，当时间变化时，先增后减.函数模型①;③④都是单调函数，所以选择函数模型②.由，得，所以，由解得所以日销售量与时间的变化关系为（3）由（2）知所以即当时，由基本不等式得，当且仅当，即时，等号成立.所以.当时，为减函数，所以，综上所述：当时，的最小值为【点睛】关键点点睛：本题考查函数模型的应用，在已知函数模型时，直接利用所给数据求出模型听参数得函数解析式．然后可根据函数解析式确定函数性质求得最值等．分段函数在求最值时需要分段求解，然后比较才能得出结论．