2020-2021学年北京市首都师大附中教育集团七年级（上）期末数学试卷

2020-2021学年北京市首都师大附中教育集团七年级（上）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分．在每小题所列出的四个选项中，只有一项是最符合题目要求的）

1．（3分）下列温度比低的是　　

A． B． C． D．

2．（3分）2020年6月23日，我国的北斗卫星导航系统星座部署完成，其中一颗中高轨道卫星高度大约是21500000米．将数字21500000用科学记数法表示为　　

A． B． C． D．

3．（3分）实数，在数轴上的位置如图所示，以下说法正确的是　　

A． B． C． D．

4．（3分）如图，经过刨平的木板上的，两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是　　

A．两点之间，线段最短 

B．两点确定一条直线 

C．垂线段最短 

D．在同一平面内，过一点有且只有一条直线与已知直线垂直

5．（3分）如图，已知射线射线，射线表示北偏西的方向，则射线表示的方向为　　

A．北偏东 B．北偏东 C．北偏东 D．东偏北

6．（3分）已知直线，将一块含角的直角三角板按如图方式放置，其中，两点分别落在直线，上，若，则的度数为　　

A． B． C． D．

7．（3分）下列等式变形中正确的是　　

A．若，则 

B．若，则 

C．若，则 

D．若，则

8．（3分）下列选项中，左边的平面图形能够折成右边封闭的立体图形的是　　

A． B． 

C． D．

9．（3分）若，则代数式的值为　　

A． B．1 C．2 D．3

10．（3分）已知：线段，点是直线上一点，直线上共有3条线段：，和．若其中有一条线段的长度是另一条线段长度的两倍，则称点是线段的“巧分点”，线段的“巧分点”的个数是　　

A．3 B．6 C．8 D．9

二、填空题（本大题共8小题，每小题2分，共16分）

11．（2分）如果，那么的余角等于　　．

12．（2分）若，则　　．

13．（2分）若单项式与的和仍是单项式，则的值是　　．

14．（2分）已知关于的方程的解是，则的值为　　．

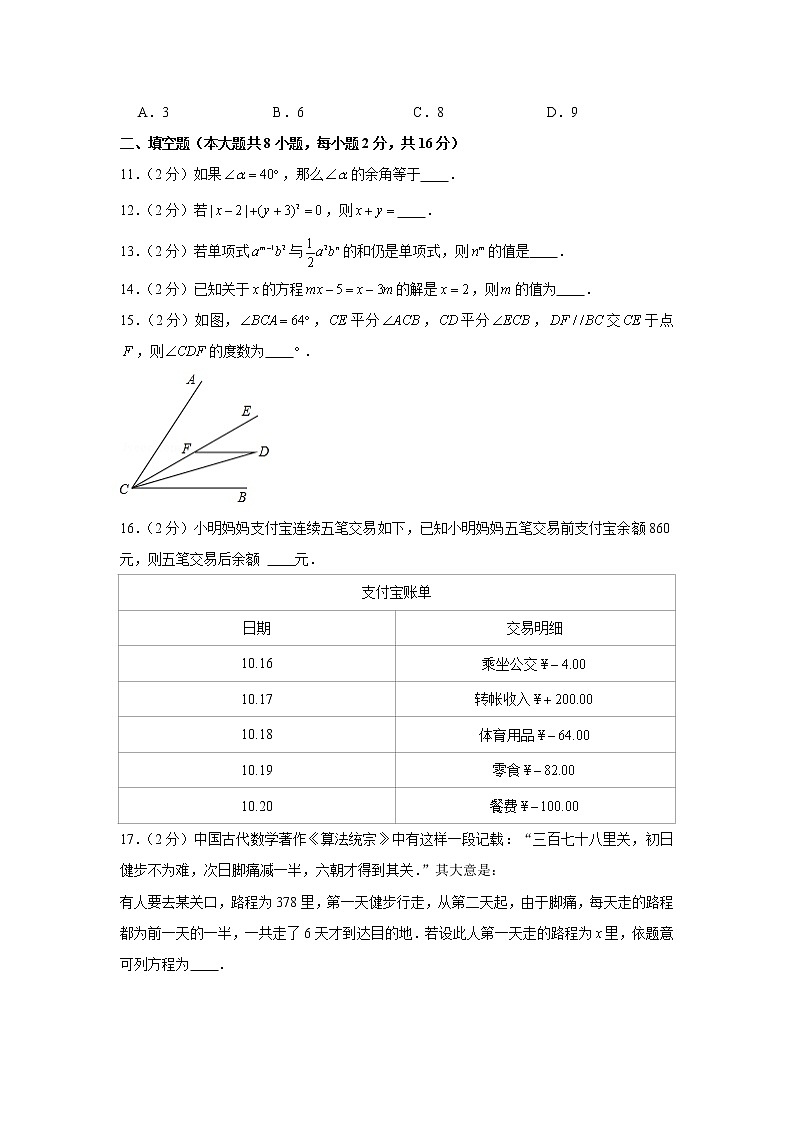
15．（2分）如图，，平分，平分，交于点，则的度数为　　．

16．（2分）小明妈妈支付宝连续五笔交易如下，已知小明妈妈五笔交易前支付宝余额860元，则五笔交易后余额 　　元．

17．（2分）中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是：

有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了6天才到达目的地．若设此人第一天走的路程为里，依题意可列方程为　　．

18．（2分），，过点作直线的垂线，点为垂足，若，则为　　度．

三、解答题（共10小题，第19，20题各8分，第21题4分，第22题5分，第23题4分，第24，25，26题各5分，第27题6分，第28题4分，共54分）

19．（8分）计算：

（1）；

（2）．

20．（8分）解方程：

（1）；

（2）．

21．（4分）如图是一个长方体纸盒的表面展开图，已知纸盒中相对两个面上的数互为相反数．

（1）填空：　　，　　；

（2）先化简，再求值：．

22．（5分）如图，点是的边上的一点．

（1）过点画的垂线，交于点；

（2）过点画的垂线，垂足为；

（3）过点画的平行线；

（4）若每个小正方形的边长是1，则点到的距离是　　；

（5）线段，，的大小关系是　　（用“”连接）．

23．（4分）在下面的括号内，填上推理的根据，

如图，，，点，分别在，上，且．

求证：．

证明：，，

，　　．

，

　　．

又．

　　．

　　．

24．（4分）已知：如图，，平分，．求证：．

25．（5分）某小组6名同学参加一次知识竞赛，共答20道题，每题分值相同，答对得分，答错或不答扣分，下面是前5名同学的得分情况（如表）

（1）表中的　　，　　；

（2）该小组第6名同学说：“这次知识竞赛我得了0分”，请问他的说法是否正确？如果正确，请求出这位同学答对了多少题；如果不正确，请说明理由．

26．（5分）“幸福是奋斗出来的”，在数轴上，若到的距离刚好是3，则点叫做的“幸福点”，若到、的距离之和为6，则叫做、的“幸福中心”

（1）如图1，点表示的数为，则的幸福点所表示的数应该是 　　；

（2）如图2，、为数轴上两点，点所表示的数为4，点所表示的数为，点就是、的幸福中心，则所表示的数可以是 　　（填一个即可）；

（3）如图3，、、为数轴上三点，点所表示的数为，点所表示的数为4，点所表示的数为8，现有一只电子蚂蚁从点出发，以2个单位每秒的速度向左运动，当经过多少秒时，电子蚂蚁是和的幸福中心？

27．（5分）已知：点在直线上，点、都在上（点在点的左侧），连接，，平分，且．

（1）如图1，求证：；

（2）如图2，点为上一点，连接，若，求的度数；

（3）在（2）的条件下，点在直线上，连接，且，若，求的度数．（要求：在备用图中画出图形后，再计算）

28．（6分）对于同一平面内以为端点的射线与，其中，给出如下定义：，，，，是内或与射线，重合的条不同的射线，这些射线与射线形成的小于平角的角的大小分别为，，，，若这条射线满足，则称这条射线为关于射线的一个基准射线族，其中为该基准射线族的基准角度．

（1）如图1，当射线与射线恰为的两条三等分线时，判断射线，，是否为关于射线的一个基准射线族？如果是，求出它的基准角度；如果不是，请说明理由；

（2）如图2，的边与射线重合，固定射线的位置不动，将以每秒的速度绕着点逆时针转动一周．当转动时间为秒时，，，，，是关于射线的一个基准射线族．

①若，求该基准射线族的基准角度的最大值；

②若的最大值等于6，直接写出的取值范围．

2020-2021学年北京市首都师大附中教育集团七年级（上）期末数学试卷

参考答案与试题解析

一、选择题（本大题共10小题，每小题3分，共30分．在每小题所列出的四个选项中，只有一项是最符合题目要求的）

1．【解答】解：根据两个负数，绝对值大的反而小可知，

所以比低的温度是．

故选：．

2．【解答】解：将21500000用科学记数法表示为，

故选：．

3．【解答】解：根据图形可知：

，

，

则；

故选：．

4．【解答】解：经过两点有且只有一条直线，

经过木板上的、两个点，只能弹出一条笔直的墨线．

故选：．

5．【解答】解：如图，，

，

，

，

射线的方向是北偏东，

故选：．

6．【解答】解：直线，

，

故选：．

7．【解答】解：、若，则，故这个选项错误；

、若，则，故这个选项正确；

、若，则，故这个选项错误；

、若，则，故这个选项错误；

故选：．

8．【解答】解：．四棱锥的展开图有四个三角形，故选项错误；

．根据长方体的展开图的特征，可得选项正确；

．正方体的展开图中，不存在“田”字形，故选项错误；

．圆锥的展开图中，有一个圆，故选项错误．

故选：．

9．【解答】解：，

原式，

故选：．

10．【解答】解：线段的3个等分点都是线段的“巧分点”．同理，在线段延长线和反向延长线也分别有3个“巧分点”．

线段的“巧分点”的个数是9个．

故选：．

二、填空题（本大题共8小题，每小题2分，共16分）

11．【解答】解：，

的余角．

故答案为：．

12．【解答】解：与，

，，

，，

．

故填．

13．【解答】解：与的和仍是单项式，

与是同类项，

，，

解得：，，

．

故答案为：8

14．【解答】解：把代入方程得：

，

解得：，

故答案为：．

15．【解答】解：，平分，

，

平分，

，

，

．

故答案为：16．

16．【解答】解：（元，

故答案为810．

17．【解答】解：设此人第一天走的路程为里，

根据题意得：．

故答案为：．

18．【解答】解：如图所示，当点在上时，

，，

，

又，

，

又，

；

如图所示，当点在的延长线上时，

，，

，

又，

，

又，

；

故答案为：10或110．

三、解答题（共10小题，第19，20题各8分，第21题4分，第22题5分，第23题4分，第24，25，26题各5分，第27题6分，第28题4分，共54分）

19．【解答】解：（1）原式

；

（2）原式

．

20．【解答】解：（1）去括号，可得：，

移项，可得：，

合并同类项，可得：，

系数化为1，可得：．

（2）去分母，可得：，

去括号，可得：，

移项，可得：，

合并同类项，可得：，

系数化为1，可得：．

21．【解答】解：（1）纸盒中相对两个面上的数互为相反数，

观察图形可知，，．

故答案为：，；

（2）原式

当，时

原式

．

22．【解答】解：（1）、（2）、（3）如图；

（4）每个小正方形的边长是1，

点到的距离是1．

故答案为：1；

（5），

，

，

，

．

故答案为：．

23．【解答】证明：，，

，（垂直定义）．

，

（同旁内角互补，两直线平行）．

又．

（平行公理推论）．

（两直线平行，同位角相等）．

故答案为：垂直定义；同旁内角互补，两直线平行；平行公理推论；两直线平行，同位角相等．

24．【解答】证明：，

，，

平分，

，

，

，，

，

，

．

25．【解答】（1）由于共有20道题，

，

由同学3可知：答对一题可得5分，

由第3位同学可知答对一题得5，设答错或不答扣分，则

从第1位同学可列方程：

，

解得：，

，

故答案为：（1）3，20

（2）设这位同学答对道题，则他答错或不答题，则

，

解得：，

因为不是整数，所以这位同学的说法不正确．

26．【解答】解：（1）的幸福点所表示的数应该是或；

（2），

，之间的所有数都是，的幸福中心．

故所表示的数可以是或或0或1或2或3或4（答案不唯一）；

（3）设经过秒时，电子蚂蚁是和的幸福中心，依题意有

①，

解得；

②，

解得．

故当经过1.75秒或4.75秒时，电子蚂蚁是和的幸福中心．

27．【解答】解：（1）平分，

，

，

，

；

（2），

，

，

，

，

，

；

（3）①如图，，，

，

，，

，

，

，

；

②如图，，，

，

，

，

，

，

，

，

，

；

或．

28．【解答】解：（1）如图射线与射线恰为的两条三等分线，，

，

，

，

射线，，是关于射线的一个基准射线族，基准角度为；

（2）①如图时，，，

，

该基准射线族的基准角是，

该基准射线族的基准角度的最大值；

②的最大值等于6，

时，存在，且时不成立，

分以下四种情况讨论：

如图3，当时，即在直线上侧，对应，

，，，在内或与射线，重合，

，2，3，4，，，

，

，当且仅当，，，与重合时取等，

，，，互不相同，

等号不成立，，

时等式不成立，

恒成立，

的最小值大于的最大值，

，即，

，，，互不相同，

时满足要求，

，

；

如图4，时，即射线的反向延长线在内部或与一边重合，

或，2，3，4，，

，

此时不存在符合条件的；

如图5，当时，及在直线下侧，对应，

，，，在内或与射线，重合，

，2，3，4，，，

，

，当且仅当，，，与重合时取等号，

，，，互不相同，

等号不成立，，

时等号不成立，

恒成立，

的最小值大于的最大值，

，

，

，，，互不相同，

时，满足要求，

，

；

如图6，当时，即射线的反向延长线在内部或与一边重合，取即可），

，2，3，4，，

，

成立，

不满足要求；

综上所述，或．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/11/25 19:51:17；用户：初中数学1；邮箱：keda1618@xyh.com；学号：39816508