北京市西城区2020-2021学年八年级上学期期末数学试题

北京市西城区2020-2021学年度第一学期期末试卷八年级数学

考生须知：

1．本试卷共6页，共三道大题，29道小题．考试时间100分钟．

2．在试卷和答题卡上准确填写学校、班级、姓名和学号．

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．

4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答．

5．考试结束时，将本试卷、答题卡一并交回．

一、选择题（第1～10题均有四个选项，符合题意的选项只有一个．）

1. 的计算结果为（    ）

A. 6 B.  C.  D. 9

【答案】B

2. 下列图形中，是轴对称图形的是（    ）

A.  B.  C.  D.

【答案】C

3. 下列运算中正确的是（    ）

A.  B.  C.  D.

【答案】D

4. 如图，在和中，，添加下列条件，不能判定这两个三角形全等的是（    ）

A. ， B. ，

C. ， D. ，

【答案】A

5. 化简分式的结果是（    ）

A.  B.  C.  D.

【答案】B

6. 如果，那么代数式的值为（    ）

A. 14 B. 9 C.  D.

【答案】A

7. 已知一次函数，且y随x的增大而减小．下列四个点中，可能是该一次函数图象与x轴交点的是（    ）

A.  B.  C.  D.

【答案】C

8. 如图，在中，点D，E分别在边，上，点A与点E关于直线对称．若，，，则的周长为（    ）

A. 9 B. 10 C. 11 D. 12

【答案】B

9. 在学校组织的秋季登山活动中，某班分成甲、乙两个小组同时开始攀登一座高的山．乙组的攀登速度是甲组的1.2倍，乙组到达顶峰所用时间比甲组少．如果设甲组的攀登速度为，那么下面所列方程中正确的是（    ）

A.  B.  C.  D.

【答案】B

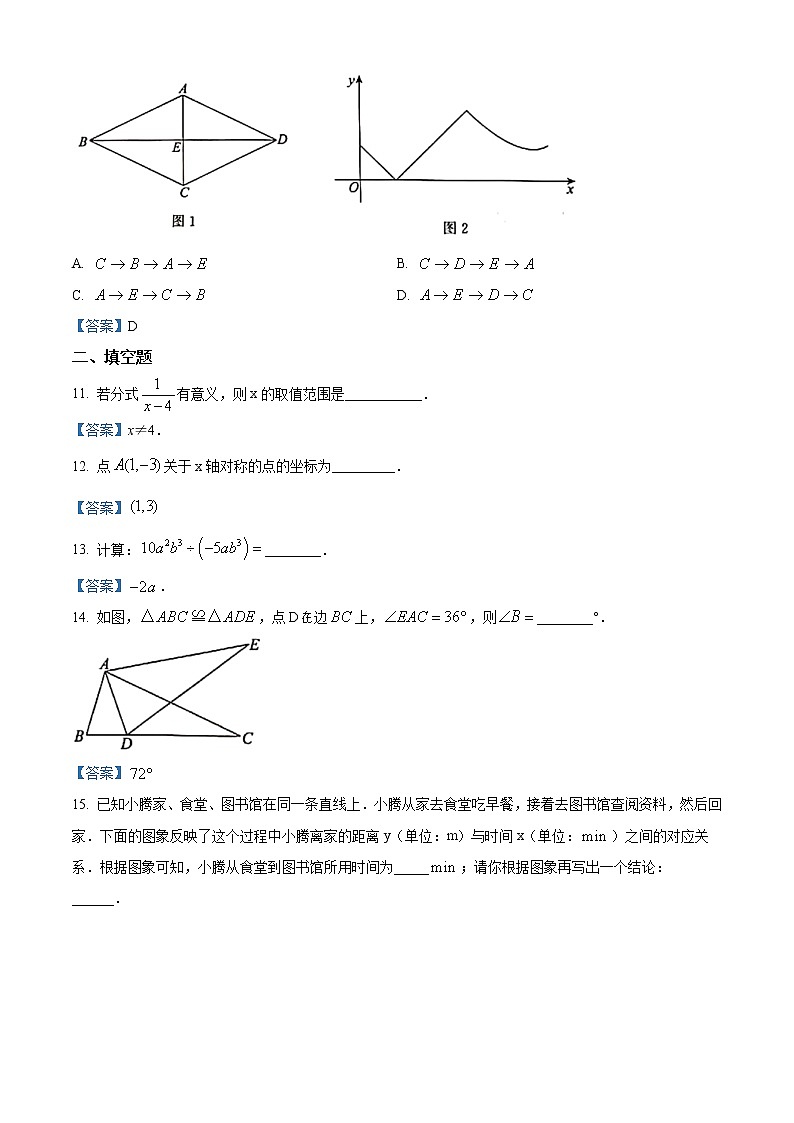
10. 如图1，四边形是轴对称图形，对角线，所在直线都是其对称轴，且，相交于点E．动点P从四边形的某个顶点出发，沿图1中的线段匀速运动．设点P运动的时间为x，线段的长为y，图2是y与x的函数关系的大致图象，则点P的运动路径可能是（    ）

A.  B.

C.  D.

【答案】D

二、填空题

11. 若分式有意义，则x的取值范围是___________．

【答案】x≠4．

12. 点关于x轴对称的点的坐标为_________．

【答案】

13. 计算：________．

【答案】．

14. 如图，，点D边上，，则________°．

【答案】

15. 已知小腾家、食堂、图书馆在同一条直线上．小腾从家去食堂吃早餐，接着去图书馆查阅资料，然后回家．下面的图象反映了这个过程中小腾离家的距离y（单位：m）与时间x（单位：）之间的对应关系．根据图象可知，小腾从食堂到图书馆所用时间为_____；请你根据图象再写出一个结论：______．

【答案】    (1). 12    (2). 食堂离图书馆780m(答案不唯一)

16. 如图1，先将边长为a的大正方形纸片剪去一个边长为b的小正方形，然后沿直线将纸片剪开，再将所得的两个长方形按如图2所示的方式拼接（无缝隙，无重叠），得到一个大的长方形．根据图1和图2的面积关系写出一个等式：________．（用含a，b的式子表示）

【答案】a2−b2＝（a＋b）（a−b）．

17. 如图，是等边三角形，于点D，于点E．若，则___；与的面积关系是：____．

【答案】    (1). ；    (2). ．

18. 如图，一次函数与的图象交于点P．下列结论中，所有正确结论的序号是_________．

①；②；③当时，；④；⑤．

【答案】②④⑤

三、解答题

19. 分解因式：

（1）；

（2）．

【答案】（1）；（2）．

20. 计算：．

【答案】

21. 小红发现，任意一个直角三角形都可以分割成两个等腰三角形．

已知：在中，．

求作：直线，使得直线将分割成两个等腰三角形．下面是小红设计的尺规作图过程．

作法：如图，①作直角边的垂直平分线，与斜边相交于点D；②作直线．所以直线就是所求作的直线．根据小红设计的尺规作图过程，

（1）使用直尺和圆规，补全图形（保留作图痕迹）；

（2）完成下面的证明．

证明：∵直线是线段的垂直平分线，点D在直线上，

∴．（_______）（填推理的依据）

∴_________________．

∵，

∴，

_________．

∴．

∴．（_______）（填推理的依据）

∴和都等腰三角形．

【答案】（1）见解析；（2）线段垂直平分线上的点到线段两个端点的距离相等；DCB，DBC；DBC；等角对等边．

22. 解方程：．

【答案】

23. 如图，，点E在的延长线上，，．

（1）求证：；

（2）连接，求证：．

【答案】（1）见解析；（2）见解析．

24. 如图，在平面直角坐标系中，直线与x轴交于点A，直线与x轴交于点B，且与直线交于点．

（1）求m和b的值；

（2）求的面积；

（3）若将直线向下平移个单位长度后，所得到的直线与直线的交点在第一象限，直接写出t的取值范围．

【答案】（1）m=2，b=4；（2）4；（3）<t<8

25. 给出如下定义：在平面直角坐标系中，已知点，这三个点中任意两点间的距离的最小值称为点的“最佳间距”．例如：如图，点的“最佳间距”是1．

（1）点，，的“最佳间距”是__________；

（2）已知点，，．

①若点O，A，B的“最佳间距”是1，则y的值为__________；

②点O，A，B的“最佳间距”的最大值为________；

（3）已知直线l与坐标轴分别交于点和，点是线段上的一个动点．当点，，的“最佳间距”取到最大值时，求此时点P的坐标．

【答案】（1）2；（2）①±1；②3；（3）P（，）．

26. 课堂上，老师提出了这样一个问题：如图1，在中，平分交于点D，且．求证：．小明的方法是：如图2，在上截取，使，连接，构造全等三角形来证明结论．

（1）小天提出，如果把小明的方法叫做“截长法”，那么还可以用“补短法”通过延长线段构造全等三角形进行证明．辅助线的画法是：延长至F，使_________，连接．请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；

（2）小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：如图3，点D在的内部，，，分别平分，，，且．求证：．请你解答小芸提出的这个问题；

（3）小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：如果在中，，点D在边上，，那么平分．小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．

【答案】（1）BD，证明见解析；（2）见解析；（3）见解析．

北京市西城区2020-2021学年度第一学期期末试卷八年级数学附加题

一、填空题

27. 我们可以将一些只含有一个字母且分子、分母的次数都为一次的分式变形，转化为整数与新的分式的和的形式，其中新的分式的分子中不含字母，如：，．参考上面的方法，解决下列问题：

（1）将变形为满足以上结果要求的形式：_________；

（2）①将变形为满足以上结果要求的形式：_________；②若为正整数，且a也为正整数，则a的值为__________．

【答案】    (1).     (2).     (3). 2或6

二、解答题

28. 如图，在平面直角坐标系中，直线与x轴的负半轴交于点A，与y轴交于点B．点C在第四象限，，且．

（1）点B坐标为_________，点C的横坐标为________；

（2）设与x轴交于点D，连接，过点C作轴于点E．若射线平分，用等式表示线段与的数量关系，并证明．

【答案】（１）(0，3)，3；（2）AD=2CE，证明见解析．

29. 在平面直角坐标系中，对于任意两点，定义如下：点M与点N“直角距离”为，记作．例如：点与的“直角距离”．

（1）已知点，则在这四个点中，与原点O“直角距离”等于1的点是__________；

（2）如图，已知点，根据定义可知线段上的任意一点与原点O的“直角距离”都等于1．若点P与原点O的“直角距离”，请在图中将所有满足条件的点P组成的图形补全；

（3）已知直线，点是x轴上的一个动点．

①当时，若直线上存在点D，满足，求k的取值范围；

②当时，直线与x轴，y轴分别交于点E，F．若线段上任意一点H都满足，直接写出t的取值范围．

【答案】（1），；（2）见解析；（3）①；②

本试卷的题干、答案和解析均由组卷网（http://zujuan.xkw.com）专业教师团队编校出品。

登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。

试卷地址：在组卷网浏览本卷

组卷网是学科网旗下的在线题库平台，覆盖小初高全学段全学科、超过900万精品解析试题。

关注组卷网服务号，可使用移动教学助手功能（布置作业、线上考试、加入错题本、错题训练）。

学科网长期征集全国最新统考试卷、名校试卷、原创题，赢取丰厚稿酬，欢迎合作。

钱老师 QQ：537008204    曹老师 QQ：713000635