人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.3 二次函数y＝a（x－h）2＋k的图象和性质学案设计

这是一份人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.3 二次函数y＝a（x－h）2＋k的图象和性质学案设计，共5页。学案主要包含了课堂笔记，课时训练等内容，欢迎下载使用。

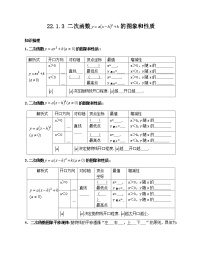
1．一般地，抛物线y＝a(x－h)2＋k与y＝ax2形状相同，位置不同．
2．把抛物线y＝ax2向上(下)向左(右)平移，可以得到抛物线y＝a(x－h)2＋k.平移的方向、距离要根据h，k的值来决定．
3．性质
(1)对称轴是________．顶点是________；
(2)当a＞0时，开口向上．当x＜h时，y随x的增大而________，当x＞h时，y随x的增大而________；
当a＜0时，开口向下．当x＜h时，y随x的增大而________，当x＞h时，y随x的增大而________；
(3)当a>0时，当x＝h时，函数取最________值为k；
当a<0时，当x＝h时，函数取最________值为________．
【课时训练】
1．将抛物线y＝2x2向上平移3个单位长度，再向右平移2个单位长度，所得到的抛物线为( )
A．y＝2(x＋2)2＋3 B．y＝2(x－2)2＋3 C．y＝2(x－2)2－3 D．y＝2(x＋2)2－3
2．二次函数y＝－3(x－2)2＋9的图象的开口方向，对称轴和顶点坐标分别为( )
A．开口向下，对称轴为x＝－2，顶点为(2，9)
B．开口向下，对称轴为x＝2，顶点为(2，9)
C．开口向上，对称轴为x＝－2，顶点为(－2，0)
D．开口向上，对称轴为x＝2，顶点为(－2，－9)
3．如图，在平面直角坐标系中，抛物线所表示的函数解析式为y＝－2(x－h)2＋k，则下列结论正确的是( )
A．h>0，k>0 B．h<0，k>0 C．h<0，k<0 D．h>0，k<0
4．设A(－2，y1)，B(1，y2)，C(2，y3)是抛物线y＝－(x＋1)2＋a上的三点，则y1，y2，y3的大小关系为( )
A．y1>y2>y3 B．y1>y3>y2 C．y3>y2>y1 D．y3>y1>y2
5．对于抛物线y＝－eq \f(1,2)(x＋1)2＋3，下列结论：①抛物线的开口向下；②对称轴为x＝1；③顶点坐标为(－1，3)；④x>1时，y随x的增大而减小．其中正确结论的个数为( )
A．1个 B．2个 C．3个 D．4个
6． 二次函数y＝(x－1)2＋3图象的顶点坐标是 ________．
7．在二次函数y＝－2(x＋3)2－1中，当x________时，y随x的增大而增大；当x________时，y随x的增大而减小；当x＝________，有最________值为________．
8． 已知点A(x1，y1)、B(x2，y2)在二次函数y＝(x－1)2＋1的图象上，若x1＞x2＞1，则y1_______y2．
9．抛物线y＝a(x＋k)2＋k，无论k取何值，顶点都在直线__ _上．
10．抛物线y＝2(x－2)2－6的顶点为C，已知y＝－kx＋3的图象经过点C，则这个一次函数图象与两坐标轴所围成的三角形面积为____．
11．在同一坐标系中，画出函数y＝eq \f(1,2)(x－1)2＋1和函数y＝eq \f(1,2)(x＋2)2－1的图象，并回答下列问题：
(1)分别指出这两条抛物线的对称轴和顶点坐标；
(2)抛物线y＝eq \f(1,2)(x＋2)2－1经过怎样的平移可得到抛物线y＝eq \f(1,2)(x－1)2＋1?
12．二次函数y＝x2的图象如图所示，请将此图象向右平移1个单位，再向下平移2个单位．
(1)画出经过两次平移后所得到的图象，并写出函数的解析式；
(2)求经过两次平移后的图象与x轴的交点坐标，指出当x满足什么条件时，函数值大于0?
13．如图，将函数y＝eq \f(1,2)(x－2)2＋1的图象沿y轴向上平移得到一条新函数的图象，其中点A(1，m)，B(4，n)平移后的对应点分别为点A′、B′.若曲线段AB扫过的面积为9(图中的阴影部分)，则新图象的函数表达式是( )
A．y＝eq \f(1,2)(x－2)2－2 B．y＝eq \f(1,2)(x－2)2＋7
C．y＝eq \f(1,2)(x－2)2－5 D．y＝eq \f(1,2)(x－2)2＋4
14．已知抛物线y＝(x＋a)2＋2a2＋3a－5.
(1)顶点在坐标轴上，求字母a的值，并指出顶点坐标；
(2)顶点在直线x＝2上，求字母a的值，并指出顶点坐标．
15．如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C、D两点．点P是x轴上的一个动点．
(1)求此抛物线的解析式；
(2)当PA＋PB的值最小时，求点P的坐标．
答案
【课堂笔记】
3．(1)x＝h (h，k) (2)减小 增大 增大 减小
(3)小 大 k
【课时训练】
1—5.BBAAC
6.(1，3)
7.＜－3 ＞－3 －3 大 －1
8.＞
9. y＝－x
10.1
11. 图象略
(1)抛物线y＝eq \f(1,2)(x－1)2＋1的对称轴为直线x＝1，顶点坐标为(1，1)；抛物线y＝eq \f(1,2)(x＋2)2－1的对称轴为直线x＝－2，顶点坐标为(－2，－1)；
(2)把抛物线y＝eq \f(1,2)(x＋2)2－1沿x轴向右平移3个单位，再沿y轴向上平移2个单位即可得到抛物线y＝eq \f(1,2)(x－1)2＋1.
12.(1)画图略．依题意得y＝(x－1)2－2＝x2－2x＋1－2＝x2－2x－1，
∴平移后图象的解析式为y＝x2－2x－1；
(2)当y＝0时，即x2－2x－1＝0，
∴(x－1)2＝2，∴x－1＝±eq \r(2)，∴x1＝1－eq \r(2)，x2＝1＋eq \r(2)，
∴平移后的图象与x轴交于两点，坐标分别为(1－eq \r(2)，0)和(1＋eq \r(2)，0)．
由图可知，当x＜1－eq \r(2)或x＞1＋eq \r(2)时，二次函数y＝x2－2x－1的函数值大于0.
13. D
14.(1)抛物线y＝(x＋a)2＋2a2＋3a－5的顶点坐标为(－a，2a2＋3a－5)，
①若顶点在x轴上，则2a2＋3a－5＝0，解得a＝1或a＝－eq \f(5,2).所以顶点坐标为(－1，0)或eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)，0)).
②若顶点在y轴上，则－a＝0，即a＝0，2a2＋3a－5＝－5.所以顶点坐标为(0，－5)；
(2)抛物线y＝(x＋a)2＋2a2＋3a－5的顶点坐标为(－a，2a2＋3a－5)，
因为顶点在直线x＝2上，所以－a＝2，a＝－2.
所以2a2＋3a－5＝－3.即a的值为－2，顶点坐标为(2，－3)．
15.(1)∵抛物线顶点坐标为(1，4)，
∴设y＝a(x－1)2＋4，由于抛物线过点B(0，3)，
∴3＝a(0－1)2＋4，解得a＝－1.
∴解析式为y＝－(x－1)2＋4，即y＝－x2＋2x＋3；
(2)作点B关于x轴的对称点E(0，－3)，连接AE交x轴于点P.
设AE解析式y＝kx＋b，则eq \b\lc\{(\a\vs4\al\c1(k＋b＝4，,b＝－3，))解得eq \b\lc\{(\a\vs4\al\c1(k＝7，,b＝－3，))
∴yAE＝7x－3，当y＝0时，x＝eq \f(3,7)，∴点P坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,7)，0)).