人教版八年级上册13.4课题学习 最短路径问题授课ppt课件

这是一份人教版八年级上册13.4课题学习 最短路径问题授课ppt课件，共21页。PPT课件主要包含了导入新课，能否给出证明，应用新知和拓展，当堂练习，课堂小结，使用要点，类型二两线一点，类型三两线两点等内容，欢迎下载使用。
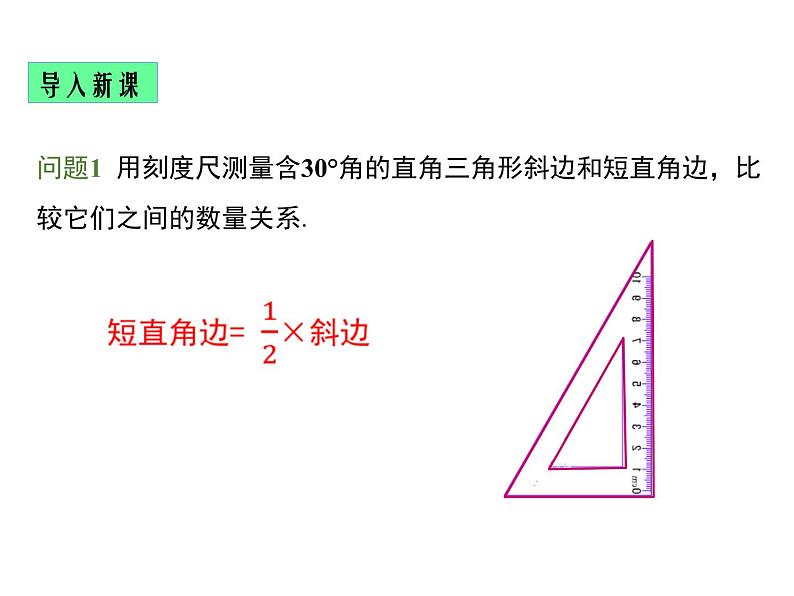
问题1 用刻度尺测量含30°角的直角三角形斜边和短直角边，比较它们之间的数量关系.
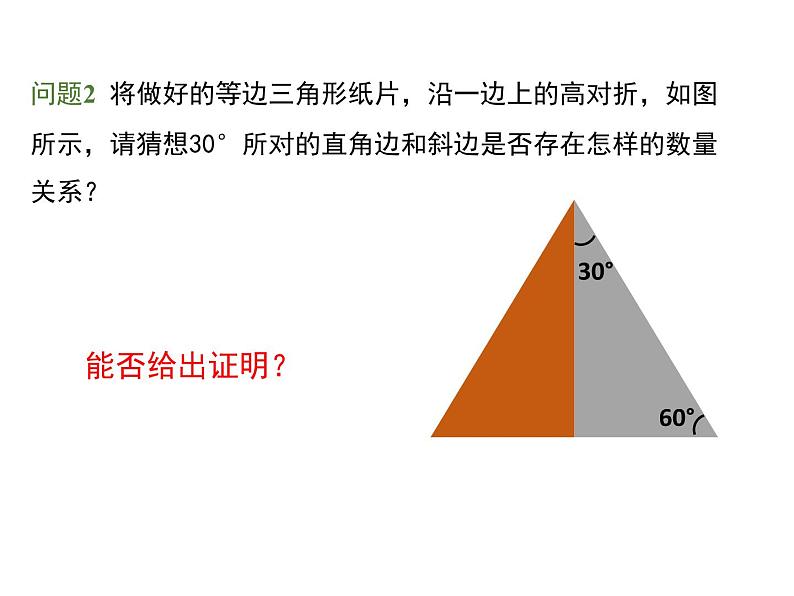
问题2 将做好的等边三角形纸片，沿一边上的高对折，如图所示，请猜想30°所对的直角边和斜边是否存在怎样的数量关系？
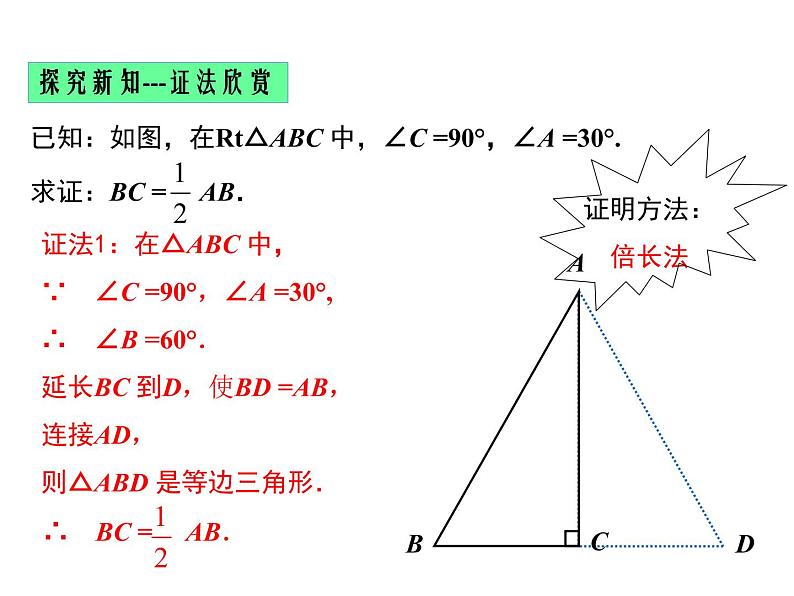
证法1：在△ABC 中，∵　∠C =90°，∠A =30°, ∴　∠B =60°．延长BC 到D，使BD =AB，连接AD，则△ABD 是等边三角形．
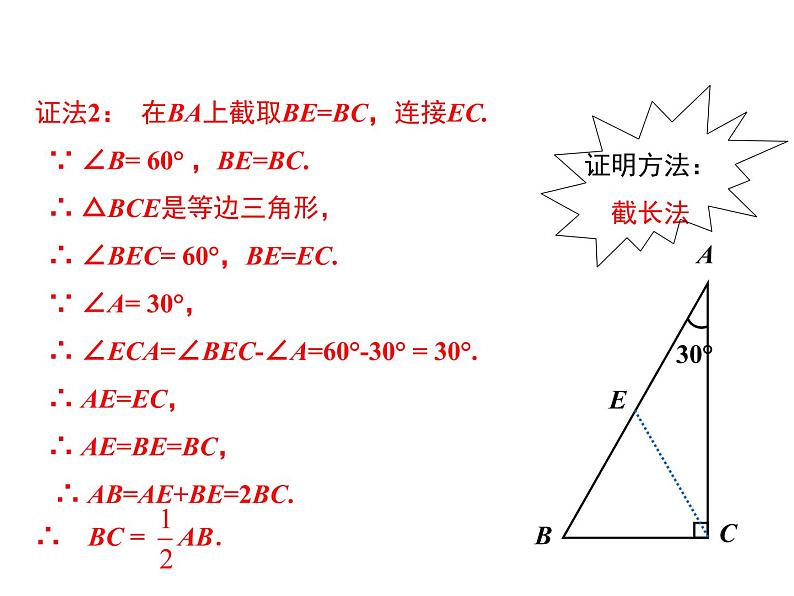
探究新知---证法欣赏
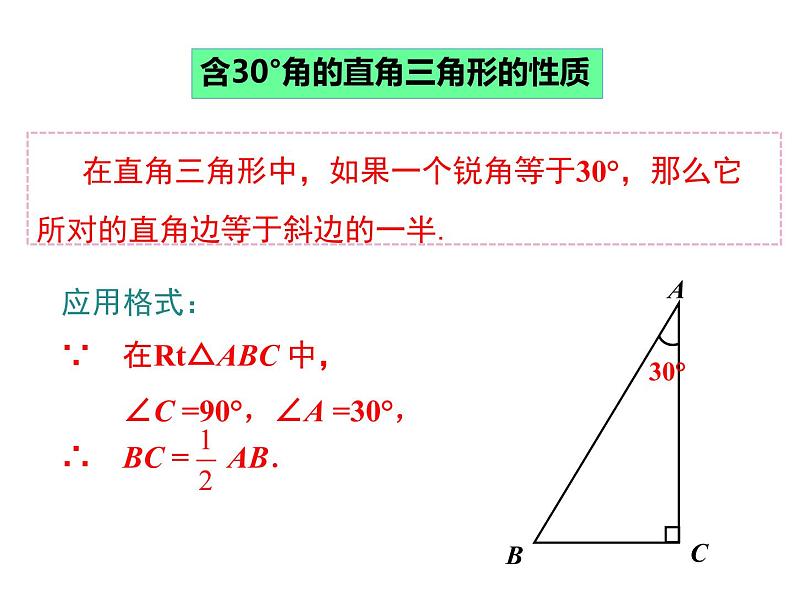
含30°角的直角三角形的性质
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
应用格式：∵　在Rt△ABC 中，　　∠C =90°，∠A =30°，　　
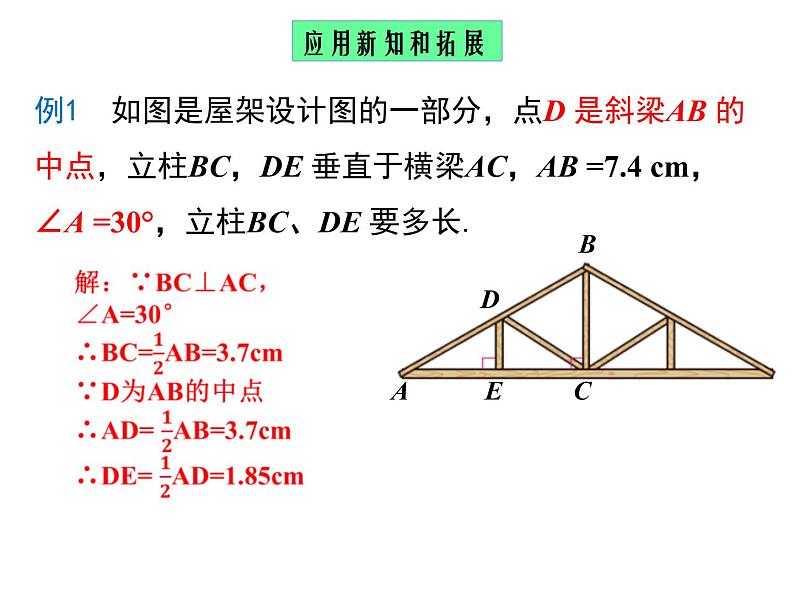
例1　如图是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC，DE 垂直于横梁AC，AB =7.4 cm，∠A =30°，立柱BC、DE 要多长.
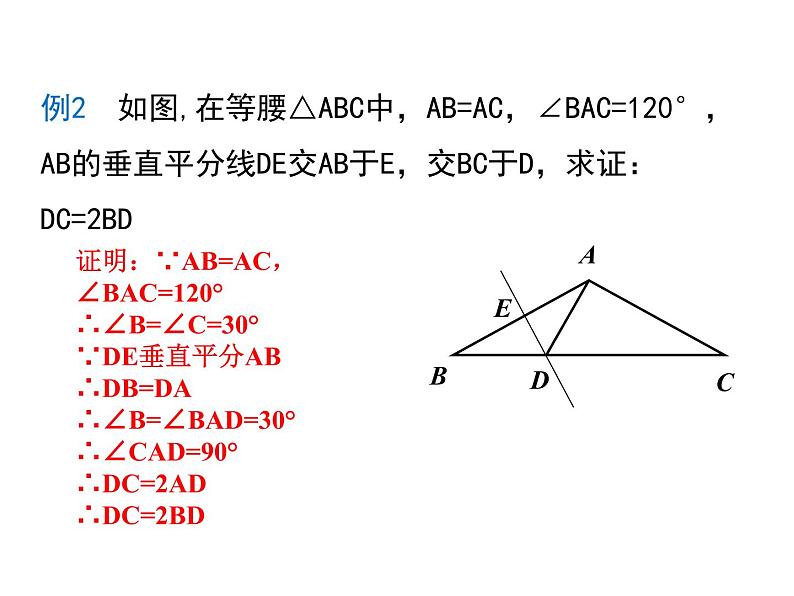
例2　如图,在等腰△ABC中，AB=AC，∠BAC=120°，AB的垂直平分线DE交AB于E，交BC于D，求证：DC=2BD
证明：∵AB=AC，∠BAC=120°∴∠B=∠C=30°∵DE垂直平分AB∴DB=DA∴∠B=∠BAD=30°∴∠CAD=90°∴DC=2AD∴DC=2BD
1.如图，在△ABC 中，∠ACB =90°，CD 是高，∠A =30°，AB =4．则BD = .
2.如图，∠AOB=30°，点D是其角平分线OC上的一点，过D作DE//OB交OA于E，作DF⊥OB，垂足为F，DF=10，则OE= .
这道题，你能否提出1-2个问题来，并完成解答？或增加一个条件，再提问？
3.如图，△ABC是等边三角形，AD=BE，BD、CE相交于M点，CN⊥BD于点N①求∠CMN的度数②若MN=3cm，求CM的长
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半
含30°角的直角三角形的性质
找准30 °的角所对的直角边，点明斜边
前提条件：直角三角形中
课题学习：最短路径问题
【问题概述】最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。【问题原型】“将军饮马”，“造桥选址”，“费马点”。【涉及知识】“两点之间线段最短”，“垂线段最短”，“三角形三边关系”，“轴对称”，“平移”。【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。【解题思路】找对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查．
问题1（将军饮马）：相传古希腊亚历山大里亚城有位久负盛名的学者，名叫海伦。有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题： 从图中的A地出发，到一条笔直的河边l饮马，然后回到B地马棚。到什么地方饮水，可使得他所走的路程全线最短？
例1.作图：如图，在直线MN上求作一点P，使得AP+BP的线段和最小，并说明理由。
类型一：两点一线（将军饮马）
同步1-1：如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长度等于BP+EP的最小值的是（ ）A. BC B. CE C. AD D. AC
例2.作图：如图，点P在∠AOB内，点E、F分别是AO,BO上的动点，请找到E、F的位置使得△PEF周长最小。
例3. 如图，八年级某班的同学举行文艺晚会，桌子摆成如图所示两直排，图中OA、OB，OA桌面放满了橘子，OB桌面放满了糖果，站在C处的小艾先拿橘子，再坐到D处座位上，请你帮他设计一条线路，使得所走总路程最短。
练习：课本93第15题