人教版八年级上册13.2 画轴对称图形综合与测试课前预习ppt课件

这是一份人教版八年级上册13.2 画轴对称图形综合与测试课前预习ppt课件，共13页。

教学目标1．理解图形轴对称变换的性质．2．能按要求画出一个平面图形关于某直线对称的图形．3．理解在平面直角坐标系中，已知点关于x 轴或y 轴对称的点的坐标的变化规律．4．掌握在平面直角坐标系中作出一个图形的轴对称图形的方法．教学重点难点画轴对称图形及点的坐标的变化规律．
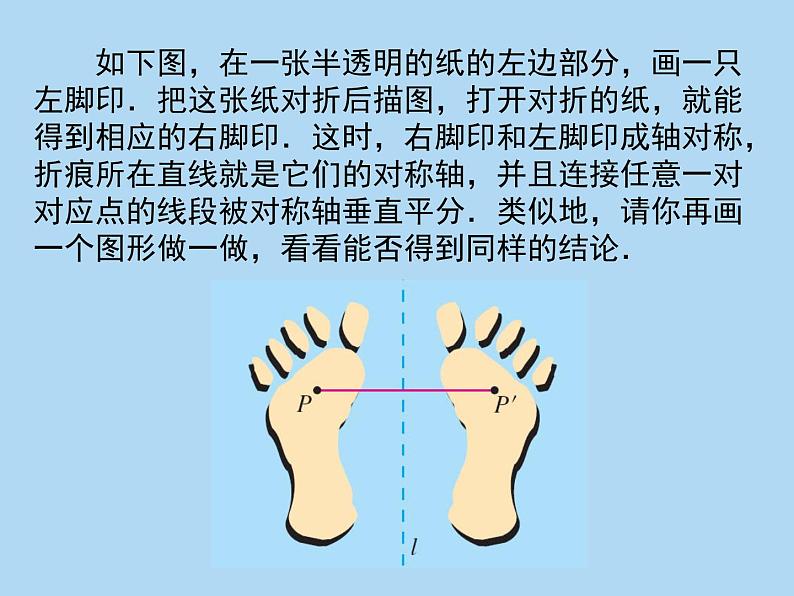
如下图，在一张半透明的纸的左边部分，画一只左脚印．把这张纸对折后描图，打开对折的纸，就能得到相应的右脚印．这时，右脚印和左脚印成轴对称，折痕所在直线就是它们的对称轴，并且连接任意一对对应点的线段被对称轴垂直平分．类似地，请你再画一个图形做一做，看看能否得到同样的结论．
归纳 由一个平面图形可以得到与它关于一条直线 l 对称的图形，这个图形与原图形的形状、大小完全相同；新图形上的每一点都是原图形上的某一点关于直线 l 的对称点；连接任意一对对应点的线段被对称轴垂直平分．
思考 如果有一个图形和一条直线，如何画出与这个图形关于这条直线对称的图形呢？
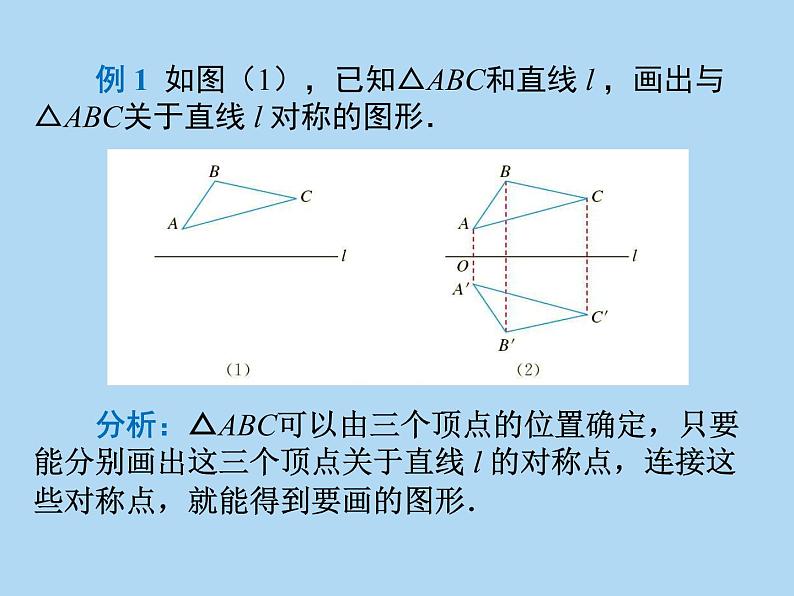
例 1 如图（1），已知△ABC和直线 l ，画出与△ABC关于直线 l 对称的图形．
分析：△ABC可以由三个顶点的位置确定，只要能分别画出这三个顶点关于直线 l 的对称点，连接这些对称点，就能得到要画的图形．
画法：（1）如图（2），过点A画直线 l 的垂线，垂足为O，在垂线上截取OA′＝OA，A′ 就是点A关于直线 l 的对称点； （2）同理，分别画出点B，C关于直线 l 的对称点B′，C′； （3）连接A′B′，B′C′，C′A′，则△A′B′C′即为所求.
归纳 几何图形都可以看作由点组成．对于某些图形，只要画出图形中的一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形．
思考 下图是一幅老北京城的示意图，其中西直门和东直门是关于中轴线对称的．如果以天安门为原点，分别以长安街和中轴线为x轴和y轴建立平面直角坐标系，根据如图所示的东直门的坐标，你能说出西直门的坐标吗？
在如下图的平面直角坐标系中，画出下列已知点及其关于坐标轴的对称点，并把它们的坐标填入表格中，看看每对对称点的坐标有怎样的规律，再和同学讨论一下．
归纳 点（x，y）关于x轴对称的点的坐标为（x，－y）； 点（x，y）关于y轴对称的点的坐标为（－x，y）．
例 2 如下图，四边形ABCD的四个顶点的坐标分别为 A(－5，1)，B(－2，1)，C(－2，5)，D(－5，4)，分别画出与四边形ABCD关于y轴和x 轴对称的图形．
解：点（x，y）关于y轴对称的点的坐标为（－x，y），因此四边形ABCD的顶点A，B，C，D关于y轴对称的点分别为A′( ， )，B′( ， )，C′( ， )，D′( ， )，依次连接A′B′，B′C′，C′D′，D′A′，就可得到与四边形ABCD关于y轴对称的四边形A′B′C′D′． 类似地，请你在图上画出与四边形ABCD关于x轴对称的图形．
对于这类问题，只要先求出已知图形中的一些特殊点（如多边形的顶点）的对称点的坐标，描出并连接这些点，就可以得到这个图形关于坐标轴对称的图形．
如图， △ABO关于x轴对称，点A的坐标为（1,－2），写出点B的坐标.