初中数学湘教版九年级下册1.1 二次函数多媒体教学课件ppt

这是一份初中数学湘教版九年级下册1.1 二次函数多媒体教学课件ppt，共17页。PPT课件主要包含了新课导入，一条直线，探究新知，yx2，左降右升，描点和连线，y＝3x2，随堂练习等内容，欢迎下载使用。

用描点法画函数图象的一般步骤是什么？
我们学过的一次函数的图象是什么图形？
①列表；②描点；③连线
那么，二次函数的图象会是什么样的图形呢？这节课我们来学习最简单的二次函数 y = ax2 的图象.
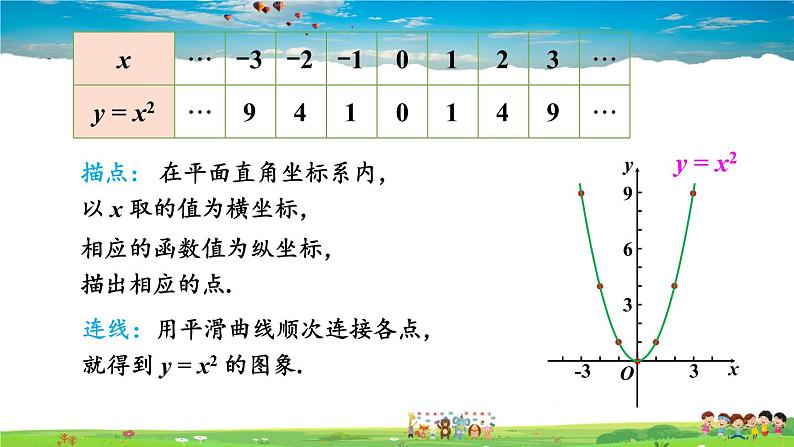
列表： 对于二次函数 y = x2， 其自变量 x 可以取任意实数. 因此让 x 取 0 和一些互为相反数的数， 并且算出相应的函数值， 列成下表：
描点： 在平面直角坐标系内，以 x 取的值为横坐标， 相应的函数值为纵坐标， 描出相应的点.
连线：用平滑曲线顺次连接各点，就得到 y = x2 的图象.
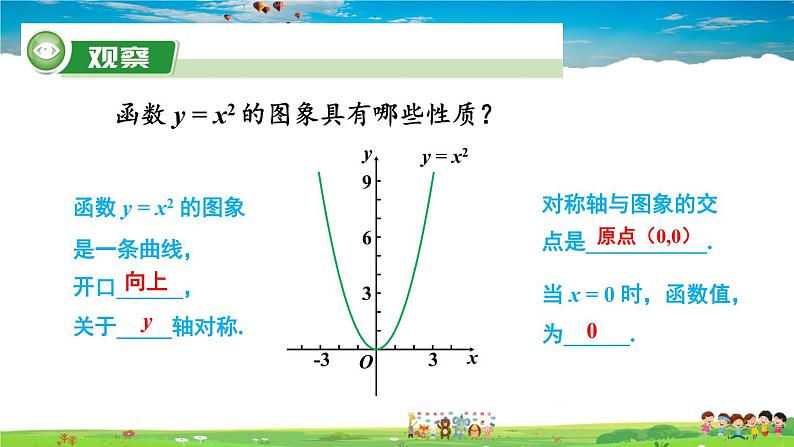
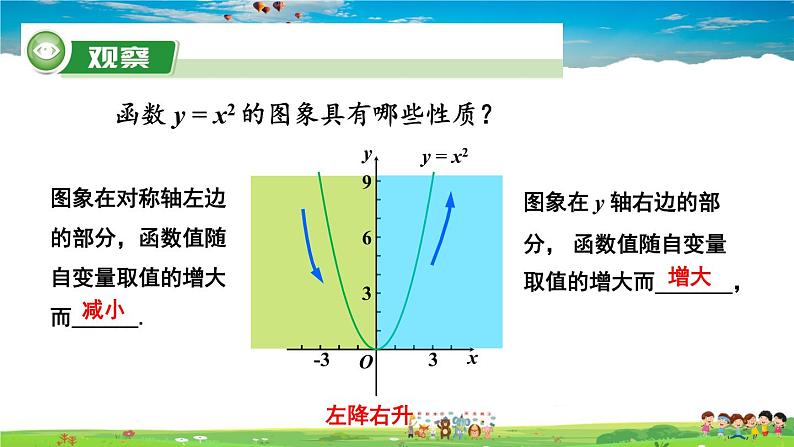
函数 y = x2 的图象具有哪些性质？
函数 y = x2 的图象是一条曲线，开口______，关于_____轴对称.
对称轴与图象的交点是___________.
当 x = 0 时，函数值，为______.
图象在对称轴左边的部分，函数值随自变量取值的增大而______.
图象在 y 轴右边的部分， 函数值随自变量取值的增大而_______，
y ＝ ax2 （a>0）图象是不是都具有上述性质呢？
按“列表、描点、连线”的步骤试一试.
y ＝ ax2（a ＞ 0 ）的图象关于 y 轴对称，可以先画出图象在 y 轴右边的部分，然后利用对称性，画出图象在 y 轴左边的部分．
解 因为二次函数 y = x2 的图象关于 y 轴对称， 因此列表时， 自变量 x 可以从原点的横坐标 0 开始取值.
利用对称性， 画出图象在 y 轴左边的对称点， 并用一条光滑曲线把 y 轴左边的点和原点顺次连接起来， 这样就得到了 y ＝ x2 的图象.
对于二次函数 y ＝ ax2 , |a| 越大, 开口______,反之开口______．
1.画出二次函数 y ＝ 6x2 的图象，并填空：（1）图象的对称轴是＿＿＿， 对称轴与图象的交点是＿＿＿＿；（2）图象的开口向＿＿＿；（3） 图象在对称轴左边的部分， 函数值随自变量取值的增大而＿＿＿；图象在对称轴右边的部分， 函数值随自变量取值的增大而＿＿＿＿．
2. 在同一直角坐标系中画出二次函数 y ＝ 3x2 及 y ＝ x2 的图象， 并比较它们的共同点与不同点.
y ＝ x2
1. 二次函数 y ＝ x2 不具有的性质是（ ） A．对称轴是 y 轴 B．开口向上 C．当x＜0时, y 随 x 的增大而减小 D．有最大值
2. 已知二次函数 y＝ax2 (a＞0)过 A (－2, y1), B (1,y2) 两点, 则下列关系式中正确的是（ ） A．y1＞0＞y2 B．y2＞0＞y1 C．y1＞y2＞0 D．y2＞y1＞0
3. 画出二次函数 y ＝ x2 的图象,并回答下列问题:（1）当 x 取何值时, y 有最小值,最小值是多少？（2）当 x＞0时, y 随 x 的增大怎样变化？ 当 x ＜ 0 时呢？
（1）当 x＝0时, y 有最小值,最小值是 0．（2）当x＞0时, y 随 x 的增大而增大; 当x＜0时, y 随 x 的增大而减小．