初中1.1 二次函数集体备课课件ppt

这是一份初中1.1 二次函数集体备课课件ppt，共19页。PPT课件主要包含了开口向下，原点00，函数图象“左升右降”，随堂练习，y＝－2x2等内容，欢迎下载使用。

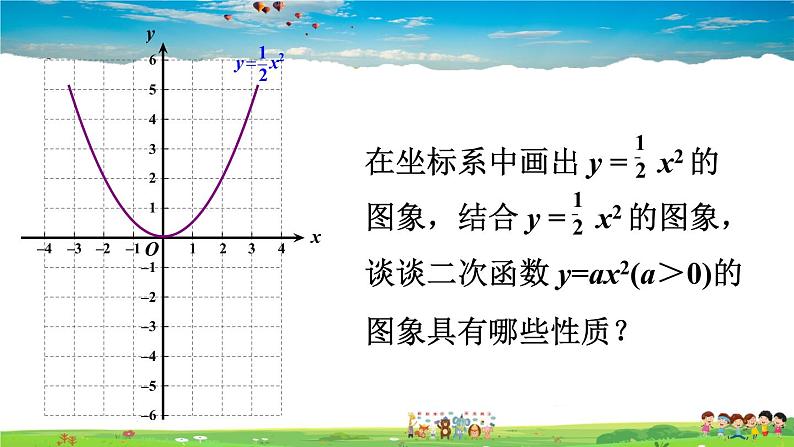
在坐标系中画出 y = x2 的图象，结合 y = x2 的图象，谈谈二次函数 y=ax2(a＞0)的图象具有哪些性质？
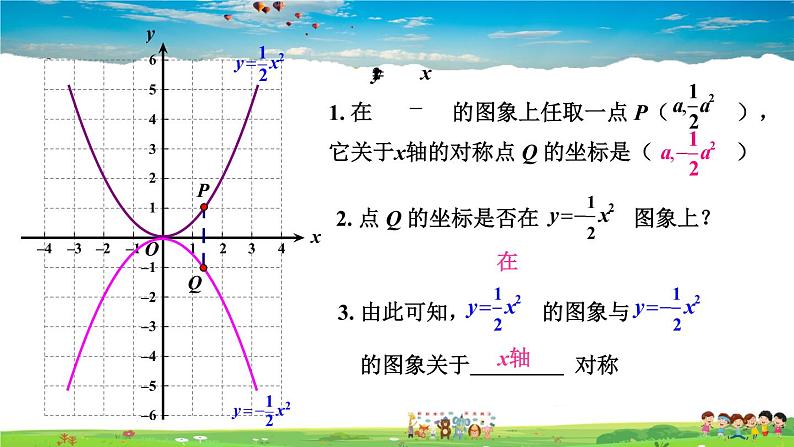
1. 在 的图象上任取一点 P（ ），它关于x轴的对称点 Q 的坐标是（ ）
2. 点 Q 的坐标是否在 图象上？
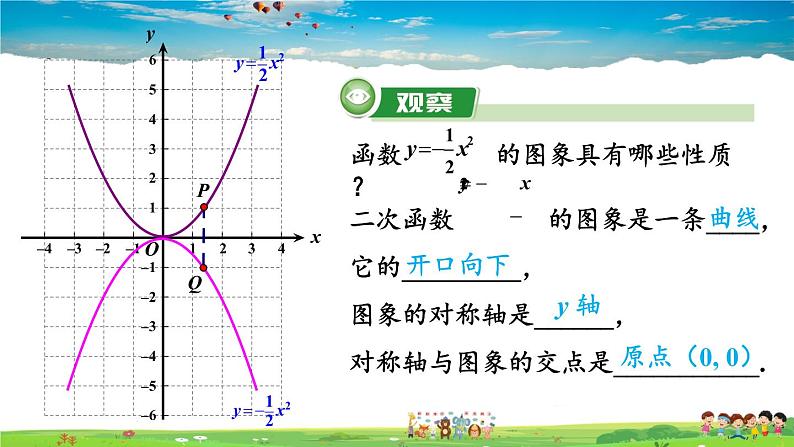
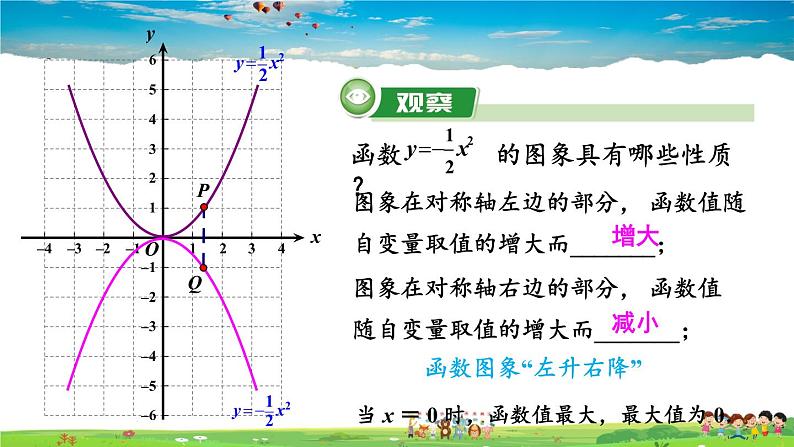
函数 的图象具有哪些性质？
图象在对称轴左边的部分， 函数值随自变量取值的增大而_______；
图象在对称轴右边的部分， 函数值随自变量取值的增大而_______；
当 x ＝ 0 时，函数值最大，最大值为 0．
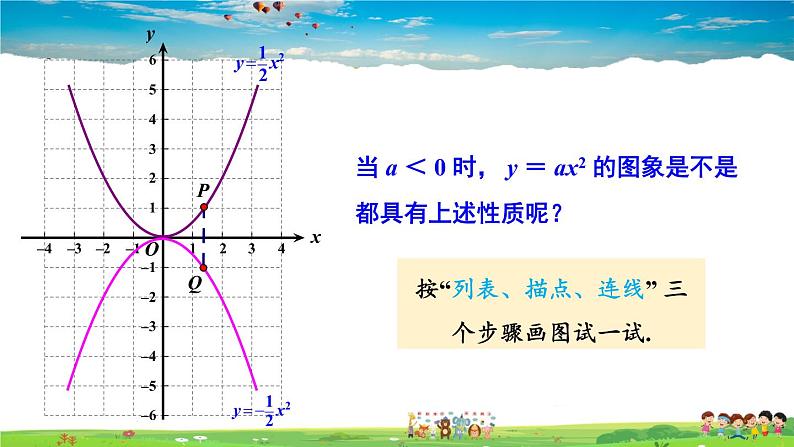
当 a ＜ 0 时， y ＝ ax2 的图象是不是都具有上述性质呢？
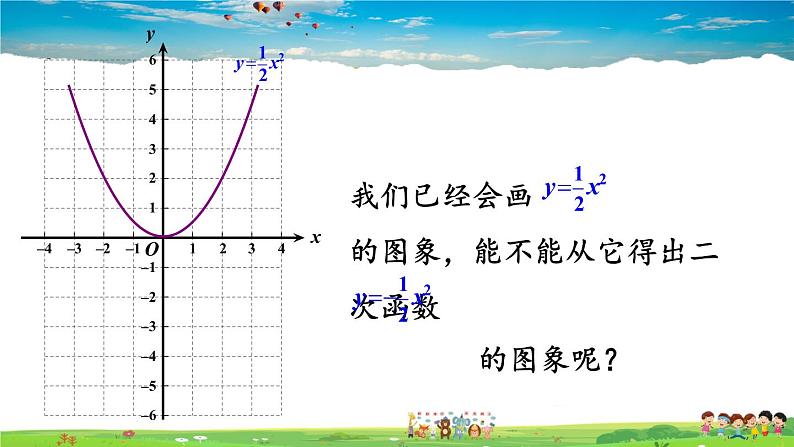
按“列表、描点、连线” 三个步骤画图试一试.
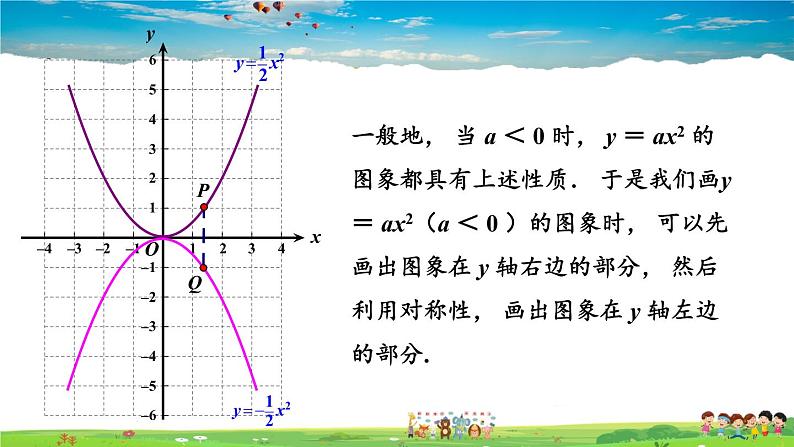
一般地， 当 a ＜ 0 时， y ＝ ax2 的图象都具有上述性质． 于是我们画y ＝ ax2（a ＜ 0 ）的图象时， 可以先画出图象在 y 轴右边的部分， 然后利用对称性， 画出图象在 y 轴左边的部分.
解 列表： 自变量 x 从原点的横坐标 0 开始取值.
描点和连线：画出图象在 y 轴右边的部分．利用对称性， 画出图象在 y 轴左边的部分.这样就得到了 的图象.
观察图 的图象跟实际生活中的什么相像？
以棒球在空中经过的路线的最高点为原点建立直角坐标系， x 轴的正方向水平向右， y 轴的正方向竖直向上， 则可以看出棒球在空中经过的路线是形如 y ＝ ax2（a ＜ 0 ）的图象的一段． 由此受到启发， 我们把二次函数 y ＝ ax2 的图象这样的曲线叫作抛物线 ，简称为抛物线 y ＝ ax2．
一般地， 二次函数 y ＝ ax2的图象关于 y 轴对称， 抛物线与它的对称轴的交点（0，0）叫作抛物线 y ＝ ax2 的顶点.
1.画出二次函数 y ＝ －10x2 的图象， 并填空：（1） 抛物线的对称轴是＿＿＿＿， 顶点坐标是＿＿＿＿＿＿；（2） 抛物线的开口向＿＿＿；（3） 抛物线在对称轴左边的部分， 函数值随自变量取值的增大而＿＿＿； 在对称轴右边的部分， 函数值随自变量取值的增大而＿＿＿＿＿．
2.在同一直角坐标系中画出二次函数 y ＝ -0.3x2 与 y ＝ -8x2 的图象， 并比较它们的共同点与不同点.
y ＝ -0.3x2
1. 下列关于抛物线 y＝－x2 的说法,错误的是（ ） A．关于 y 轴对称 B．与抛物线 y＝x2 关于原点对称 C．画抛物线 y＝－x2 时,只要先画出 y 轴右边的部分,然后利用对称性,再画出图象在y 轴左边的部分即可 D．抛物线有一个最低点,其坐标为（0,0）
2. 抛物线 y ＝2x2, y ＝－2x2, y ＝ x2 的共同特征是（ ） A．开口都向上,且都关于 y 轴对称 B．开口都向下,且都关于 x 轴对称 C．顶点都是原点,且都关于 y 轴对称 D．顶点都是原点,且都关于 x 轴对称
3. 若二次函数 y ＝ ax2 (a ≠ 0)的图象过点 P (2,－8),则函数的表达式为___________,抛物线有最____点,当 x______时, y 随 x 的增大而增大．