初中数学湘教版九年级下册1.1 二次函数图片ppt课件

这是一份初中数学湘教版九年级下册1.1 二次函数图片ppt课件，共18页。PPT课件主要包含了探究新知，解配方，教材P17页，顶点坐标是，教材P18页，顶点坐标，最小值，顶点坐标-34，最小值4，随堂练习等内容，欢迎下载使用。

画出 的图象.
故对称轴是直线 ， 顶点坐标是 .
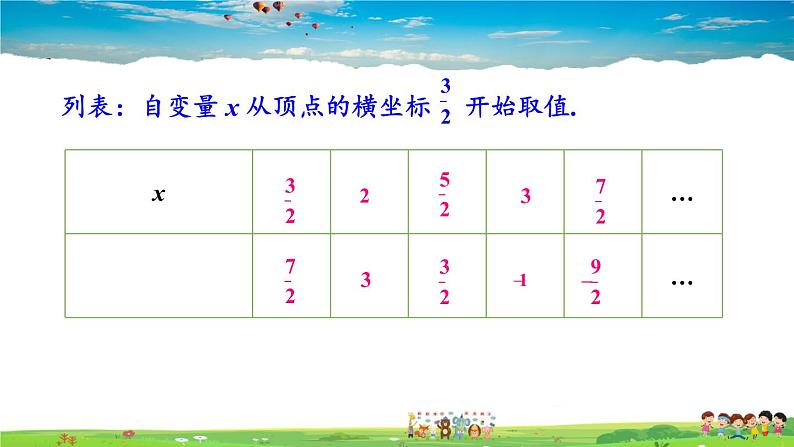
列表：自变量 x 从顶点的横坐标 开始取值.
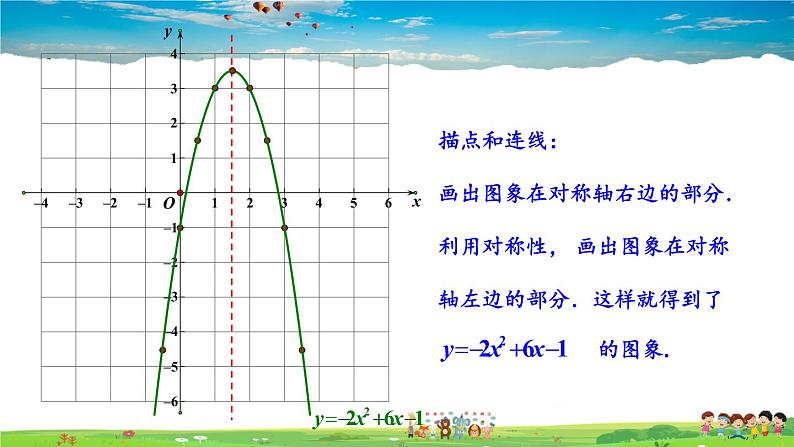
描点和连线：画出图象在对称轴右边的部分．利用对称性， 画出图象在对称轴左边的部分．这样就得到了 的图象.
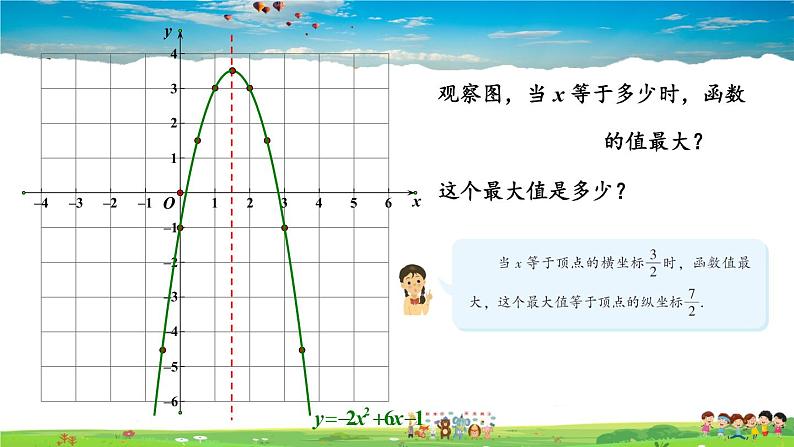
观察图，当 x 等于多少时，函数 的值最大？这个最大值是多少？
一般地， 有下述结论： 二次函数 y ＝ ax2 ＋ bx ＋ c， 当 x 等于顶点的横坐标时， 达到最大值（a ＜ 0 ）或最小值（a ＞ 0 ）， 这个最大（小）值等于顶点的纵坐标．
求二次函数 的最大值．
顶点坐标（2,1），于是当 x = 2 时，y达到最大值 1．
根据下列关系你能发现二次函数 y=ax2+bx+c 的图象和性质吗？
因此，当 时，函数达到最大值（a < 0）或最小值（a > 0）:
1. 写出下列二次函数图象的对称轴、顶点坐标和开口方向，并画出它们的图象. （1） ； （2） .
（1）对称轴 x = 1，顶点坐标（1,-2），开口向上
（2）对称轴 x = 2，顶点坐标（2,2），开口向下
2. 求下列二次函数图象的顶点坐标以及最大值或 最小值： （1） ； （2）
将二次函数 y ＝ x2＋2x－1 的图象沿 x 轴向右平移 2 个单位, 得到的函数表达式是（ ） A．y＝(x＋3)2－2 B．y＝(x＋3)2＋2 C．y＝(x－1)2＋2 D．y＝(x－1)2－2
2. 已知二次函数 y ＝ a(x －1)2＋b (a ≠ 0)有最小值－1, 则 a 与 b 之间的大小关系是（ ） A．a＜b B．a ＝ b C．a＞b D．不能确定
3. 若一次函数 y ＝ (a＋1) x＋a 的图象过第一、三、四象限, 则二次函数 y＝ax2－ax（ ） A．有最大值 B．有最大值－ C．有最小值 D．有最小值－
4. 已知抛物线 y＝－x2＋2x＋2． （1）通过配方求出它的对称轴、顶点坐标，并画出该抛物线； （2）若该抛物线上两点 A (x1 , y1), B(x2 , y2)的横坐标满足 x1＞x2＞1, 试比较 y1 与 y2 的大小．
解：（1）配方：y ＝－x2＋2x＋2 ＝－（x－1）2＋3对称轴是直线 x = －1，顶点坐标是（1,3）
用配方法求二次函数 y = ax2 + bx + c 的顶点坐标、对称轴；