2020-2021学年2.3 垂径定理教案配套ppt课件

这是一份2020-2021学年2.3 垂径定理教案配套ppt课件，共15页。PPT课件主要包含了新课导入，垂径定理，教材P59页，随堂练习等内容，欢迎下载使用。

如图，1400年前，我国隋代建造的赵州桥的桥拱是圆弧形， 它的跨度（弧所对的弦长）是 37.4 m， 拱高（弧的中点到弦的距离）为 7.2 m， 求桥拱的半径（精确到 0.1 m）.
在⊙O中，AB 是任一条弦，CD 是⊙O 的直径，且 CD ⊥ AB，垂足为 E. 试问：AE 与 BE， 与 ， 与 分别相等吗？
因为圆是轴对称图形， 将 ⊙O 沿直径CD对折，AE 与 BE 重合， ， 分别与 , 重合， 即AE = BE ， , .
你能试着证明这个结论吗？
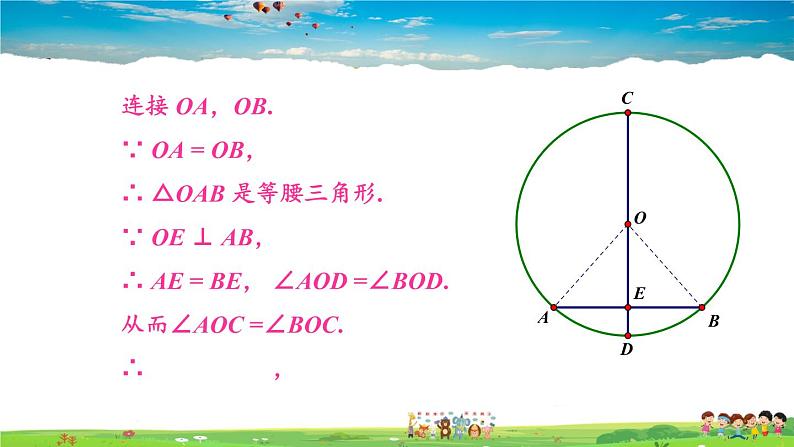
连接 OA，OB.∵ OA = OB，∴ △OAB 是等腰三角形.∵ OE ⊥ AB，∴ AE = BE， ∠AOD =∠BOD.从而∠AOC =∠BOC.∴ ，
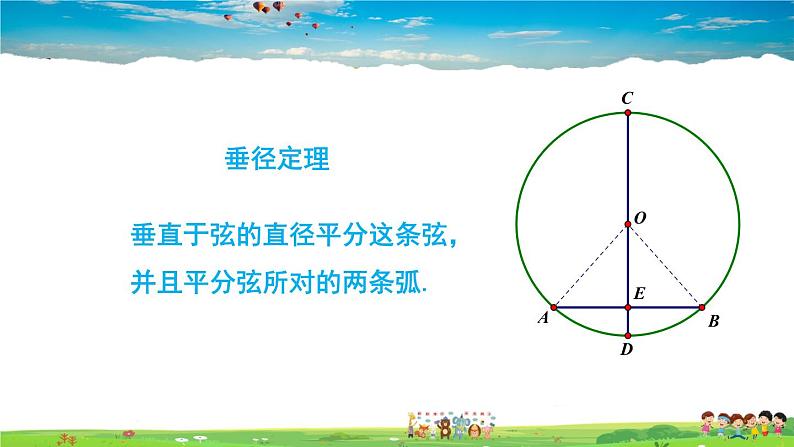
垂直于弦的直径平分这条弦， 并且平分弦所对的两条弧.
如图，弦AB = 8 cm，CD是⊙O 的直径，CD⊥AB， 垂足为 E，DE ＝ 2 cm，求⊙O 的直径 CD 的长.
解 连接 OA. 设 OA = r cm， 则 OE ＝ r - 2 （cm）.∵ CD⊥AB，由垂径定理得在 Rt△AEO 中， 由勾股定理得OA2 ＝ OE2 + AE2.即 r2 ＝ （r-2）2 + 42.解得 r ＝ 5 .∴ CD = 2r = 10 （cm）.
证明：圆的两条平行弦所夹的弧相等．已知：如图， 在⊙O 中，弦 AB 与弦 CD 平行．求证：
证明： 作直径 EF⊥ AB，∴ .又∵AB∥CD， EF ⊥ AB ，∴ EF ⊥ CD. ∴ .因此 . 即 .
如图， AB 是⊙O 的直径， C 是⊙O上一点，AC ＝ 8 cm， AB ＝ 10 cm， OD⊥BC于点 D， 求 BD 的长.
解 ∵AB是⊙O的直径，∴∠ACB=90°；∵OD⊥BC，∴OD∥AC，又∵AO=OB，∴OD是△ABC的中位线，即BD= BC；Rt△ABC中，AB = 10cm，AC = 8cm；由勾股定理，得：BC=6cm；故BD= BC=3cm．
1. 如图,☉O 的直径为 10 , 弦 AB 的长为 6 , M 是弦 AB 上 的一动点, 则线段 OM 的取值范围是（ ） A. 3 ≤ OM ≤ 5 B. 4 ≤ OM ≤ 5 C. 3＜OM ＜5 D. 4＜ OM ＜ 5
2. 一根水平放置的圆柱形输水管道横截面如图所示, 其中有水部分水面宽 0.8 m、水深 0.2 m, 则此输水 管道的直径是（ ） A. 0.4 m B. 0.5 m C. 0.8 m D. 1 m
3. 如图, 圆弧形拱桥的跨度 AB＝12 m, 拱高 CD＝ 4 m, 则拱桥的半径为（ ） A. 6.5m B. 9m C. 13 m D. 15 m
4. （分类讨论题）已知☉O 的半径为 13 cm, 弦AB ∥CD , AB＝24 cm, CD ＝10 cm, 则 AB , CD 之间的距离为 _____________．
17 cm 或 7 cm