数学八年级上册2.5 全等三角形课文ppt课件

这是一份数学八年级上册2.5 全等三角形课文ppt课件，共26页。PPT课件主要包含了知识回顾，推进新课，B′′，A′′，C′′，B′B，∵BC＝B′C′，又∵BAB′A′，B′B′′，边角边定理等内容，欢迎下载使用。
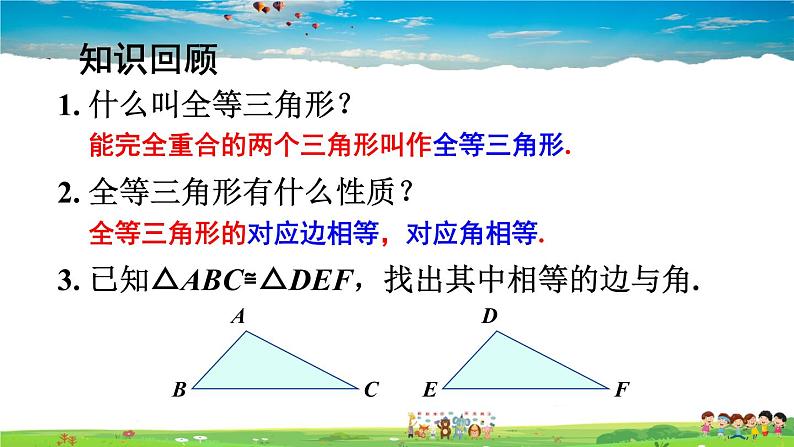
1. 什么叫全等三角形？
能完全重合的两个三角形叫作全等三角形.
2. 全等三角形有什么性质？
全等三角形的对应边相等，对应角相等.
3. 已知△ABC≌△DEF，找出其中相等的边与角.
思考：一个三角形包括三条边、三个内角共六个元素，那么两个三角形至少需要满足其中的几组元素相等才能说明它们全等呢？
下面我们来探讨这个问题.
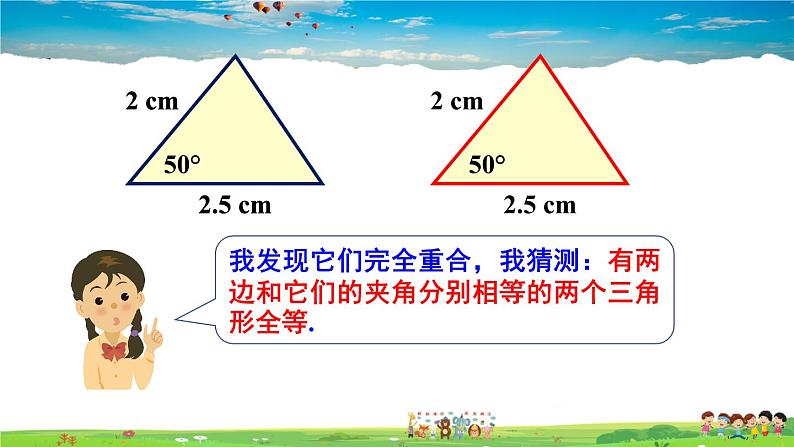
每位同学在纸上的两个不同位置分别画一个三角形，它的一个角为50°，夹这个角的两边分别为2cm，2.5cm. 将这两个三角形叠在一起，它们完全重合吗？由此你能得到什么结论？
我发现它们完全重合，我猜测：有两边和它们的夹角分别相等的两个三角形全等.
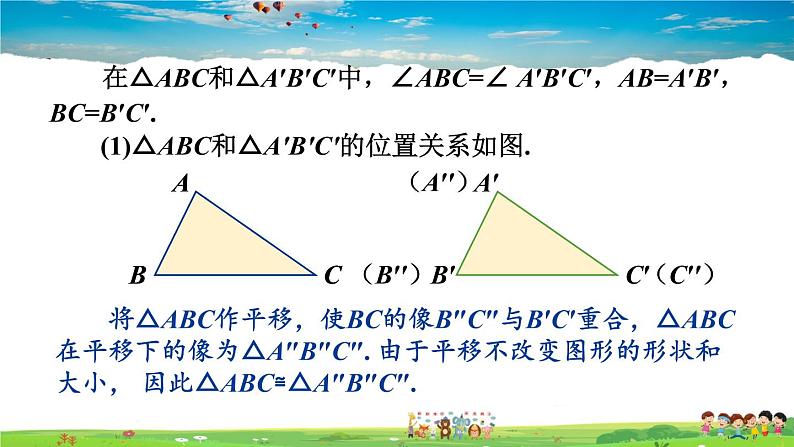
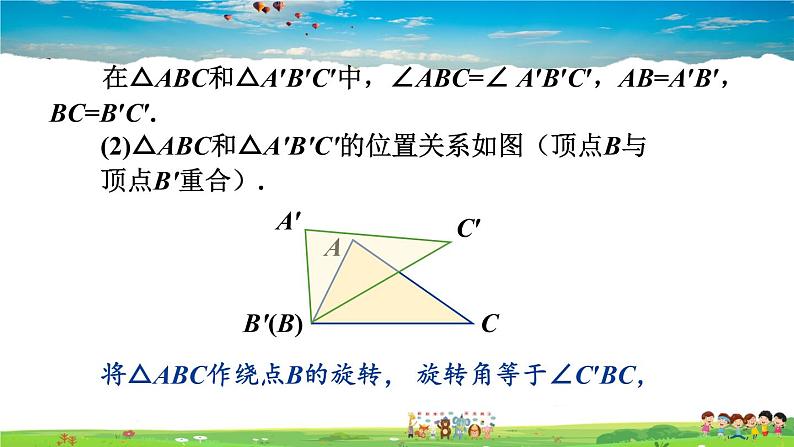
在△ABC和△A′B′C′中，∠ABC=∠ A′B′C′，AB=A′B′， BC=B′C′.
(1)△ABC和△A′B′C′的位置关系如图.
将△ABC作平移，使BC的像B″C″与B′C′重合，△ABC在平移下的像为△A″B″C″. 由于平移不改变图形的形状和大小， 因此△ABC≌△A″B″C″.
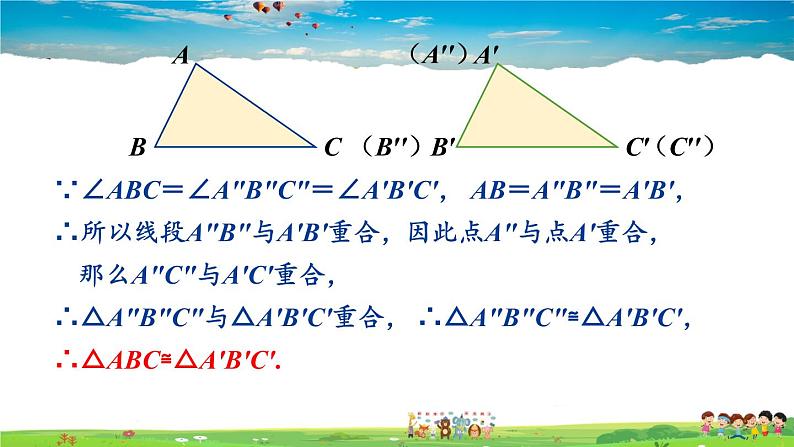
∵∠ABC＝∠A″B″C″＝∠A′B′C′， AB＝A″B″＝A′B′，
∴所以线段A″B″与A′B′重合，
因此点A″与点A′重合，
那么A″C″与A′C′重合，
∴△A″B″C″与△A′B′C′重合，
∴△A″B″C″≌△A′B′C′，
∴△ABC≌△A′B′C′.
(2)△ABC和△A′B′C′的位置关系如图（顶点B与顶点B′重合）.
将△ABC作绕点B的旋转， 旋转角等于∠C′BC，
∴线段BC的像与线段B′C′重合.
∵∠ABC＝∠A′B′C′，
∴∠C′BC =∠A′BA.
∴在上述旋转下， BA 的像与B′A′重合，
从而AC的像就与A′C′重合，
于是△ABC的像就是△A′B′C′.
由于旋转不改变图形的形状和大小，
(3)△ABC和△A′B′C′的位置关系如图.
将△ABC作平移， 使顶点B的像B″和顶点B′重合，
根据情形(1)，(2)的结论得△A″B″C″≌△A′B′C′，
因此△ABC≌△A′B′C′.
(4)△ABC和△A′B′C′的位置关系如图.
将△ABC作关于直线BC的轴反射，
△ABC在轴反射下的像为A′′BC，由于轴反射不改变图形的形状和大小，
因此△ABC≌△A′′BC，
根据情形(3)的结论得△A′′BC≌△A′B′C′，
由此得到判定两个三角形全等的基本事实：
两边及其夹角分别相等的两个三角形全等.(可简写成“边角边”或“SAS”).
　　归纳概括“SAS”判定方法: 两边和它们的夹角分别相等的两个三角形全等（可简写成“边角边”或“SAS ”）．
几何语言：在△ABC 和△ A′B′ C′中，
∴△ABC ≌△ A′B′C′（SAS）．
已知：如图，AB和CD相交于点O，且AO＝BO，CO＝DO.
求证：△ACO≌△BDO.
证明 在△ACO和△BDO中，
∴ △ACO≌△BDO.（SAS）
1.准备条件：证全等时要用的间接条件要先证好；
2.三角形全等书写三步骤：
（1）写出在哪两个三角形中；
（2）摆出三个条件用大括号括起来；
1. 如图， 将两根钢条AA′和BB′的中点O连在一起， 使钢条可以绕点O自由转动， 就可做成测量工件内槽宽度的工具（卡钳）. 只要量出A′B′的长，就得出工件内槽的宽AB. 这是根据什么道理呢？
∵AA′，BB′的中点O连在一起，
∴OA=OA′ ，OB=OB′ ，
∵∠AOB=∠A′OB′，
∴△OAB≌△OA′B′．
所以用的判定定理是边角边．
2.如图，AD∥BC，AD＝BC. 问：△ADC和△CBA是全等三角形吗？为什么？
证明 ∵AD∥BC，
∴∠DCA=∠BAC，
在△ADC和△CBA中，
3.已知：如图，AB＝AC，点E，F分别是AC，AB的中点. 求证：BE=CF.
证明 ∵AB=AC，点E，F分别是AC，AB的中点，
∴2AF=AB，2AE=AC，
在△ABE和△ACF中，
∴ △ABE≌△ACF.（SAS）
1.下列命题错误的是（ ）A.周长相等的两个等边三角形全等B.两条直角边对应相等的两个直角三角形全等C.有两条边对应相等的两个等腰三角形不一定全等D.有两条边和一个角对应相等的两个三角形全等
2.如图，AB = AC，若想用“SAS”判定△ABD≌△ACE，则需补充一个条件_________.
3.已知：如图AB = AC，AD = AE，∠BAC=∠DAE，求证： △ABD≌△ACE.
证明：∵∠BAC =∠DAE，∴∠BAC+∠CAD =∠DAE +∠CAD，即∠BAD =∠CAE，在△ABD和△ACE中，∴△ABD≌△ACE（SAS）.