初中数学2.7 角的和与差优秀ppt课件

这是一份初中数学2.7 角的和与差优秀ppt课件，共17页。

1.理解余角、补角概念，能熟练求出一个角的余角或补角．2.探索并掌握同角（等角）的余角相等，同角（等角）的补角相等的性质．
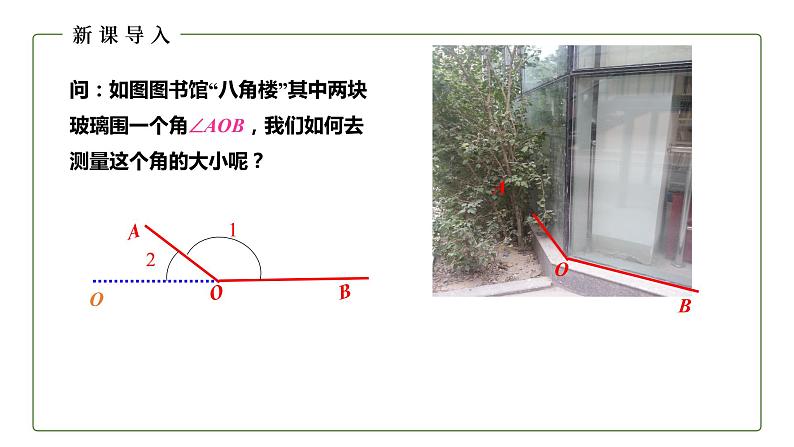
问：如图图书馆“八角楼”其中两块玻璃围一个角AOB，我们如何去测量这个角的大小呢？
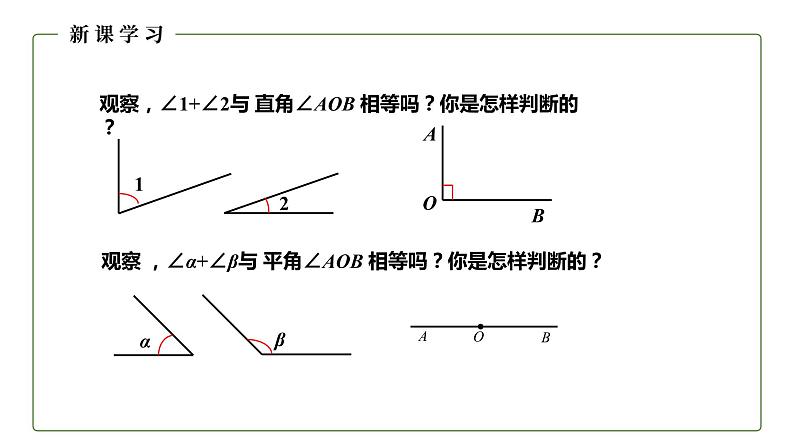
观察，∠1+∠2与 直角∠AOB 相等吗？你是怎样判断的？
观察 ，∠α+∠β与 平角∠AOB 相等吗？你是怎样判断的？
如果两个锐角的和是一个直角，我们就说这两个角互为余角，简称互余，也可以说其中一个角是另一个角的余角．互余的数学表达式：∠α ＋∠β ＝ 90 °．
如∠1与∠2互为余角， ∠1是∠2的余角，∠2也是∠1的余角．数学表达式：∠1＋∠2＝ 90 °（∠1＝90 °－∠2 或∠2＝90 °－∠1 ）．
如果两个角的和是一个平角，我们就说这两个角互为补角，简称互补，也可以说其中一个角是另一个角的补角．互补的数学表达式为: ∠α＋∠β ＝180 °．
如图，∠AOC与∠BOC互为补角，∠AOC是∠BOC的补角，∠BOC也是∠AOC的补角． 表达式：∠AOC＋∠BOC＝180°（或∠AOC＝180°-∠BOC ， ∠BOC＝ 180°-∠BOC．
1．定义中的“互为”一词如何理解？
2．互补、互余的两角是否一定有公共顶点或公共边？
如果1与2互余，那么1的余角是2，2的余角是1．
互补或互余的两角不一定有公共顶点或公共边．
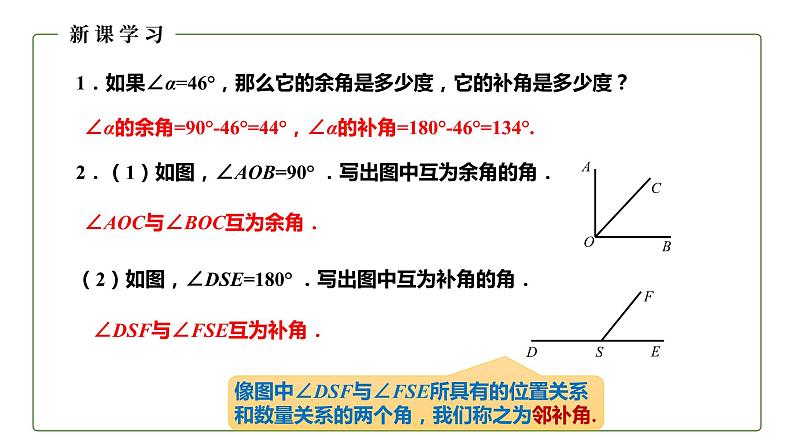
1．如果∠α=46°，那么它的余角是多少度，它的补角是多少度？
∠α的余角=90°-46°=44°，∠α的补角=180°-46°=134°.
∠AOC与∠BOC互为余角．
∠DSF与∠FSE互为补角．
像图中∠DSF与∠FSE所具有的位置关系和数量关系的两个角，我们称之为邻补角.
判断正误：1．钝角没有余角，但一定有补角．( )2．一个锐角的余角一定比这个角大．( )3．若两个角互补，则一个为锐角，一个为钝角． ( )4．若一个角的余角是45°，则这个角的补角是135°．( )
1．如果∠1和∠2都是∠α的余角，那么∠1和∠2相等吗？说明你的理由．
相等．因为∠1是∠α的余角，所以∠1+∠α=90°，所以∠1=90° -∠α．因为∠2是∠α的余角，所以∠2+∠α=90°，所以∠2=90° -∠α ，所以∠1=∠2 ．
2．如果∠3和∠4都是∠β的补角，那么∠3和∠4相等吗？说明你的理由．
相等．因为∠3是∠β的补角，所以∠3 +∠β =180°，所以∠3=180° -∠β ．因为∠4是∠β的补角，所以∠4+∠β =180°，所以∠4=180° -∠β，所以∠3=∠4．
同角(等角)的余角相等．
若∠α+∠β=90°，∠β+∠γ=90°，则∠α=∠γ．
若∠α+∠β=180°，∠β+∠γ=180°，则∠α=∠γ．
同角（等角）的补角相等．
解：因为∠AOC＝∠BOD＝90°，所以∠AOB＋∠BOC＝∠COD＋∠BOC＝90°，所以∠AOB，∠COD都是∠BOC的余角，所以∠AOB＝∠COD．因为∠AOB＝40°，所以∠COD＝40°．
1．若一个角为75°，则它的余角的度数为（　）A．285° B．105° C．75° D．15°2．已知∠A=70°，则∠A的补角为（　）A．110° B．70° C．30° D．20°3．如图，已知∠AOC=90°，下列说法正确的有（　）①∠COE=90°；②∠AOB+∠BOC=∠COE；③∠AOE=2∠COE；④∠DOE是锐角．A．1个 B．2个 C．3个 D．4个
4．已知 ∠α=63°18′，∠β是∠α的余角． （1）求∠β的度数．（2）求∠β的补角的度数．
解：（1）因为∠β是∠α的余角，所以∠α +∠β=90° ，所以∠β=90° -∠α= 90° -63°18′=26°42′ ．
（2）因为∠β +∠β的补角=180°，所以∠β的补角=180°-∠β=180°-26°42′= 153°18′．
5 ．如图，O是直线AB上一点，OC为任一条射线，OD平分∠BOC，OE平分∠AOC．（1）指出图中∠AOD的补角，∠BOE的补角；（2）若∠BOC=68°，求∠COD和∠EOC的度数．
解：（1）∠AOD的补角为∠BOD，∠BOE的补角为∠AOE；
1．互余、互补的概念：如果两个锐角的和是一个直角，我们就说这两个角互为余角，简称互余．如果两个角的和是一个平角，我们就说这两个角互为补角，简称互补．
2．性质：同角(等角)的余角相等；同角(等角)的补角相等．