山东省济南市长清区2021-2022学年九年级上学期期中数学【试卷+答案】

这是一份山东省济南市长清区2021-2022学年九年级上学期期中数学【试卷+答案】，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年山东省济南市长清区九年级第一学期期中
数学试卷
一、选择题（本大题共12个小题，每小题4分，共48分）
1．方程x（x﹣2）＝0的解是（　　）
A．x1＝x2＝﹣2 B．x1＝0，x2＝2 C．x1＝0，x2＝﹣2 D．无实数根
2．如图所示，圆柱的主视图是（　　）

A． B．
C． D．
3．不透明布袋中装有除颜色外均相同的1个红球和2个白球，搅匀后从中摸出一个球，则摸到白球的概率是（　　）
A． B． C． D．
4．用配方法解方程x2﹣6x﹣4＝0，下列配方正确的是（　　）
A．（x﹣3）2＝13 B．（x+3）2＝13 C．（x﹣6）2＝4 D．（x﹣3）2＝5
5．a、b、c、d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，则线段d的长为（　　）
A．3cm B．4cm C．5cm D．6cm
6．如图所示，某校数学兴趣小组利用标杆BE测量物的高度，已知标杆BE高1.5m，测得AB＝1.2m，AC＝14m，则建筑物CD的高是（　　）

A．17.5m B．17m C．16.5m D．18m
7．关于x的一元二次方程（m﹣1）x2﹣2x﹣1＝0有两个不相等的实数根，则实数m的取值范围是（　　）
A．m≥0且m≠1 B．m＞0 C．m≥0 D．m＞0且m≠1
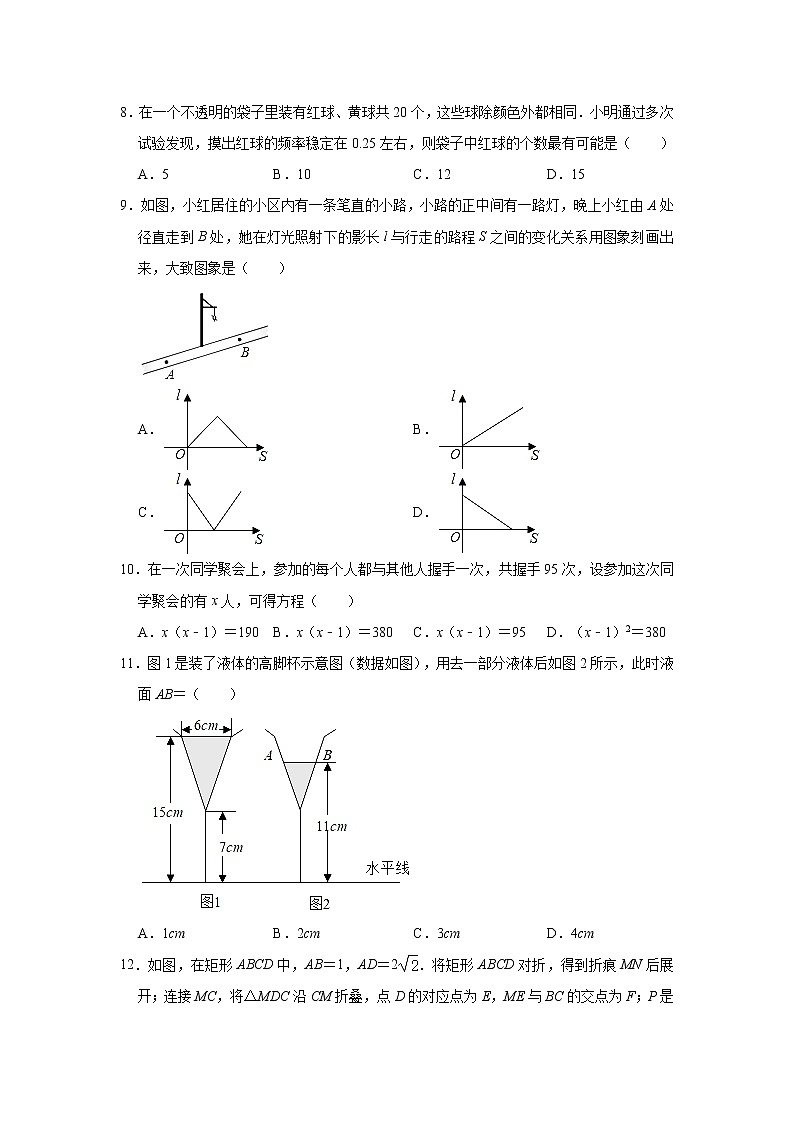
8．在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（　　）
A．5 B．10 C．12 D．15
9．如图，小红居住的小区内有一条笔直的小路，小路的正中间有一路灯，晚上小红由A处径直走到B处，她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来，大致图象是（　　）

A． B．
C． D．
10．在一次同学聚会上，参加的每个人都与其他人握手一次，共握手95次，设参加这次同学聚会的有x人，可得方程（　　）
A．x（x﹣1）＝190 B．x（x﹣1）＝380 C．x（x﹣1）＝95 D．（x﹣1）2＝380
11．图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB＝（　　）

A．1cm B．2cm C．3cm D．4cm
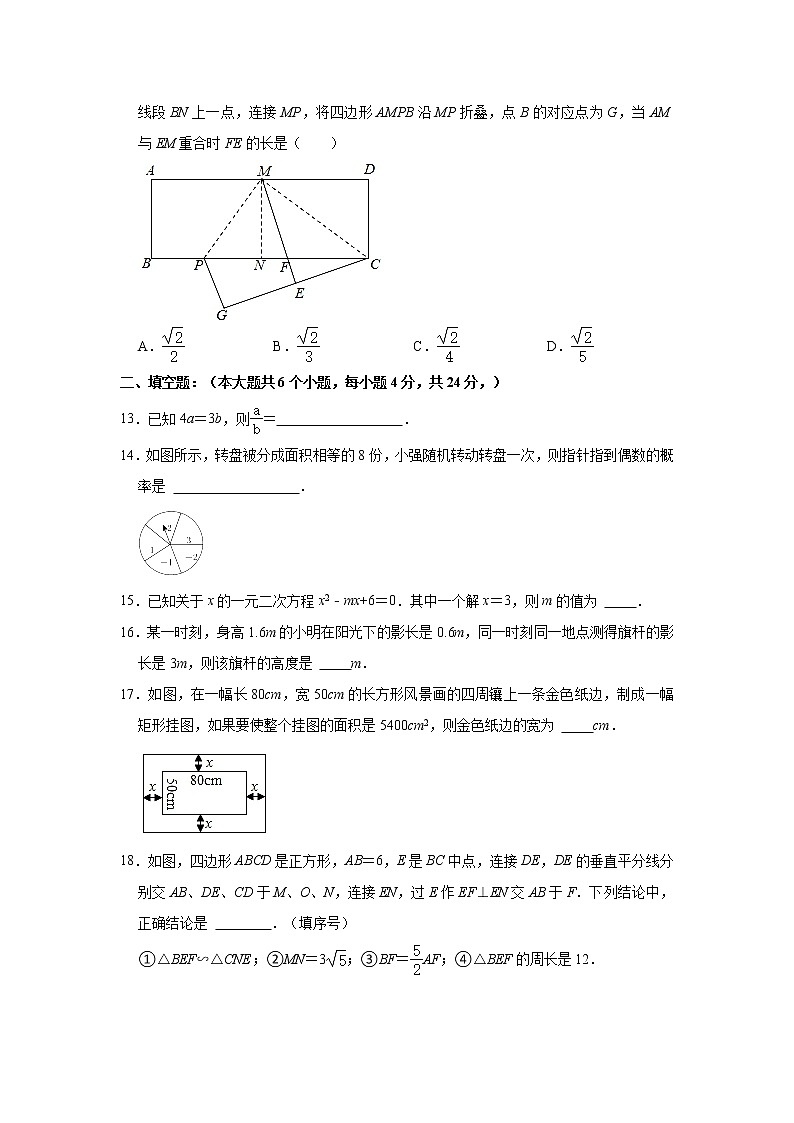
12．如图，在矩形ABCD中，AB＝1，AD＝2．将矩形ABCD对折，得到折痕MN后展开；连接MC，将△MDC沿CM折叠，点D的对应点为E，ME与BC的交点为F；P是线段BN上一点，连接MP，将四边形AMPB沿MP折叠，点B的对应点为G，当AM与EM重合时FE的长是（　　）

A． B． C． D．
二、填空题：（本大题共6个小题，每小题4分，共24分，）
13．已知4a＝3b，则＝　 　．
14．如图所示，转盘被分成面积相等的8份，小强随机转动转盘一次，则指针指到偶数的概率是 　 　．

15．已知关于x的一元二次方程x2﹣mx+6＝0．其中一个解x＝3，则m的值为 　 　．
16．某一时刻，身高1.6m的小明在阳光下的影长是0.6m，同一时刻同一地点测得旗杆的影长是3m，则该旗杆的高度是 　 　m．
17．如图，在一幅长80cm，宽50cm的长方形风景画的四周镶上一条金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是5400cm2，则金色纸边的宽为 　 　cm．

18．如图，四边形ABCD是正方形，AB＝6，E是BC中点，连接DE，DE的垂直平分线分别交AB、DE、CD于M、O、N，连接EN，过E作EF⊥EN交AB于F．下列结论中，正确结论是 　 　．（填序号）
①△BEF∽△CNE；②MN＝3；③BF＝AF；④△BEF的周长是12．

三、解答题：（本大题共9个小题，共78分解答应写出文字说明、证明过程或演算步骤。）
19．解方程：x2﹣4x＝3．
20．如图，l1∥l2∥l3，AB＝5，DE＝4，EF＝8，求AC的长．

21．如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示．
（1）请你通过画图确定灯泡所在的位置．
（2）如果小明的身高AB＝1.6m，他的影子长AC＝1.4m，且他到路灯的距离AD＝2.1m，求灯泡的高．


22．已知：如图，在正方形ABCD中，P是BC上的点，Q是CD上的点，且AQ⊥PQ，△ADQ与△QCP是否相似？并证明你的结论．

23．如图，O为原点，B，C两点坐标分别为（3，﹣1）（2，1）．
（1）以O为位似中心在y轴左侧将△OBC放大两倍，并画出图形；
（2）分别写出B，C两点的对应点B′，C′的坐标；
（3）已知M（x，y）为△OBC内部一点，写出M的对应点M′的坐标．

24．汽车产业的发展，有效促进了我国现代化建设，某汽车销售公司2018年盈利1500万元，到2020年盈利2160万元，且从2018年到2020年，每年盈利的年增长率相同．
（1）求每年盈利的年增长率；
（2）若该公司盈利的年增长率继续保特不变，那么2021年该公司盈利能否达到2500万元？
25．2019年12月以来，湖北省武汉市部分医院陆续发现不明原因肺炎病例，现已证实该肺炎为一种新型冠状病毒感染的肺炎，其传染性较强．为了有效地避免交叉感染，需要采取以下防护措施：①戴口罩；②勤洗手；③少出门；④重隔离；⑤捂口鼻；⑥谨慎吃．某公司为了解员工对防护措施的了解程度（包括不了解、了解很少、基本了解和很了解），通过网上问卷调查的方式进行了随机抽样调查（每名员工必须且只能选择一项），并将调查结果绘制成如下两幅统计图．

请你根据上面的信息，解答下列问题
（1）本次共调查了　 　名员工，条形统计图中m＝　 　；
（2）若该公司共有员工1000名，请你估计“不了解”防护措施的人数；
（3）在调查中，发现有4名员工对防护措施“很了解”，其中有3名男员工、1名女员工．若准备从他们中随机抽取2名，让其在公司群内普及防护措施，用画树状图或列表法求恰好抽中一男一女的概率（要求画出树状图或列出表格）．
26．如图，在Rt△ABC中，AC＝4cm，BC＝3cm，点P由点B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC方向向点C匀速运动，速度为1cm/s，连接PQ．设运动的时间为t（s），其中0＜t＜4．解答下列问题：
（1）AP＝　 　，AQ＝　 　；（用含t的代数式麦示）
（2）当t为何值时，以P、Q、A为顶点的三角形与△ABC相似？
（3）点P、Q在运动过程中，△APQ能否成为等腰三角形？若能，求出此时t的值；若不存在，请说明理由．


27．（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝4，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为　 　；
（2）【拓展研究】在（1）的条件下，如果正方形CDEF绕点C旋转，当点B，E，F三点共线时，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）【问题发现】当正方形CDEF旋转到B，E，F三点共线时，求线段AF的长．



参考答案
一、选择题（本大题共12个小题，每小题4分，共48分）
1．方程x（x﹣2）＝0的解是（　　）
A．x1＝x2＝﹣2 B．x1＝0，x2＝2 C．x1＝0，x2＝﹣2 D．无实数根
【分析】根据已知方程得到两个关于x的一元一次方程，解之即可．
解：∵x（x﹣2）＝0，
∴x＝0或x﹣2＝0，
解得x1＝0，x2＝2，
故选：B．
2．如图所示，圆柱的主视图是（　　）

A． B．
C． D．
【分析】根据主视图是从正面看得到的图形，可得答案．
解：从正面看，是一个矩形．
故选：B．
3．不透明布袋中装有除颜色外均相同的1个红球和2个白球，搅匀后从中摸出一个球，则摸到白球的概率是（　　）
A． B． C． D．
【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．
解：∵一个不透明的布袋中装有1个红球和2个白球，共3个球，
∴从布袋中随机摸出一个球是白球的概率为；
故选：C．
4．用配方法解方程x2﹣6x﹣4＝0，下列配方正确的是（　　）
A．（x﹣3）2＝13 B．（x+3）2＝13 C．（x﹣6）2＝4 D．（x﹣3）2＝5
【分析】方程常数项移到右边，两边加上9变形得到结果即可．
解：方程x2﹣6x﹣4＝0变形得：x2﹣6x＝4，
配方得：x2﹣6x+9＝13，即（x﹣3）2＝13，
故选：A．
5．a、b、c、d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，则线段d的长为（　　）
A．3cm B．4cm C．5cm D．6cm
【分析】利用比例线段的定理得到3：2＝6：d，然后利用比例的性质求d即可．
解：根据题意得a：b＝c：d，即3：2＝6：d，
所以d＝＝4（cm）．
故选：B．
6．如图所示，某校数学兴趣小组利用标杆BE测量物的高度，已知标杆BE高1.5m，测得AB＝1.2m，AC＝14m，则建筑物CD的高是（　　）

A．17.5m B．17m C．16.5m D．18m
【分析】根据题意和图形，利用三角形相似，可以计算出CD的长，从而可以解答本题．
解：∵EB⊥AC，DC⊥AC，
∴EB∥DC，
∴△ABE∽△ACD，
∴＝，
∵BE＝1.5m，AB＝1.2m，AC＝14m，
∴＝，
解得，DC＝17.5（m），
即建筑物CD的高是17.5m，
故选：A．
7．关于x的一元二次方程（m﹣1）x2﹣2x﹣1＝0有两个不相等的实数根，则实数m的取值范围是（　　）
A．m≥0且m≠1 B．m＞0 C．m≥0 D．m＞0且m≠1
【分析】根据一元二次方程的定义和判别式的意义得到不等式组，然后解不等式组即可求出m的取值范围．
解：∵关于x的一元二次方程（m﹣1）x2﹣2x﹣1＝0有两个不相等的实数根，
∴，
解得m＞0且m≠1．
故选：D．
8．在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（　　）
A．5 B．10 C．12 D．15
【分析】设袋子中红球有x个，根据摸出红球的频率稳定在0.25左右列出关于x的方程，求出x的值，从而得出答案．
解：设袋子中红球有x个，
根据题意，得：＝0.25，
解得x＝5，
∴袋子中红球的个数最有可能是5个，
故选：A．
9．如图，小红居住的小区内有一条笔直的小路，小路的正中间有一路灯，晚上小红由A处径直走到B处，她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来，大致图象是（　　）

A． B．
C． D．
【分析】根据中心投影的性质得出小红在灯下走的过程中影长随路程之间的变化，进而得出符合要求的图象．
解：∵小路的正中间有一路灯，晚上小红由A处径直走到B处，她在灯光照射下的影长l与行走的路程S之间的变化关系应为：
当小红走到灯下以前：l随S的增大而减小；
当小红走到灯下以后再往前走时：l随S的增大而增大，
∴用图象刻画出来应为C．
故选：C．
10．在一次同学聚会上，参加的每个人都与其他人握手一次，共握手95次，设参加这次同学聚会的有x人，可得方程（　　）
A．x（x﹣1）＝190 B．x（x﹣1）＝380 C．x（x﹣1）＝95 D．（x﹣1）2＝380
【分析】设共有x人参加联欢会，每人与其他人只握一次手，则每个人需要握（x﹣1）次手，x个人一共需要握手x（x﹣1）次，握手是在两人之间进行，所以共握x（x﹣1）÷2次，已知共要握手95次，由此可得等量关系式：x（x﹣1）÷2＝95，解此方程即得多少人参加联欢会．
解：设共有x人参加联欢会，可得方程：
x（x﹣1）÷2＝190，
x（x﹣1）＝380．
故选：B．
11．图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB＝（　　）

A．1cm B．2cm C．3cm D．4cm
【分析】高脚杯前后的两个三角形相似．根据相似三角形的判定和性质即可得出结果．
解：如图：过O作OM⊥CD，垂足为M，过O作ON⊥AB，垂足为N，

∵CD∥AB，
∴△CDO∽ABO，即相似比为，
∴＝，
∵OM＝15﹣7＝8（cm），ON＝11﹣7＝4（cm），
∴＝，
∴AB＝3cm，
故选：C．
12．如图，在矩形ABCD中，AB＝1，AD＝2．将矩形ABCD对折，得到折痕MN后展开；连接MC，将△MDC沿CM折叠，点D的对应点为E，ME与BC的交点为F；P是线段BN上一点，连接MP，将四边形AMPB沿MP折叠，点B的对应点为G，当AM与EM重合时FE的长是（　　）

A． B． C． D．
【分析】根据翻折变换的性质以及勾股定理可在直角三角形PCG中求出PG，再根据相似三角形的判定和性质得出EF＝FG即可．
解：由翻折变换可知，AM＝MD＝AD＝，AB＝GE＝1，CD＝CE＝1，
在Rt△PGC中，
设PG＝x，则BP＝x，PC＝2﹣x，由勾股定理得，
PG2+CG2＝PC2，
即x2+22＝（2﹣x）2，
解得x＝，
即FG＝，
又∵∠G＝∠FEC＝90°，∠PCG＝∠FCE，
∴△FCG∽△FCE，
∴＝＝，
∴EF＝PG＝，
故选：C．
二、填空题：（本大题共6个小题，每小题4分，共24分，）
13．已知4a＝3b，则＝　　．
【分析】根据比例的性质直接求解即可．
解：∵4a＝3b，
＝；
故答案为：．
14．如图所示，转盘被分成面积相等的8份，小强随机转动转盘一次，则指针指到偶数的概率是 　　．

【分析】根据几何概率的定义，面积比即为概率．图中偶数所占面积与总面积的比值就是转盘指向偶数的概率．
解：∵转盘被分成面积相等的8份，其中偶数有2份，
∴指针指到偶数的概率是＝．
故答案为：．
15．已知关于x的一元二次方程x2﹣mx+6＝0．其中一个解x＝3，则m的值为 　5　．
【分析】把x＝3代入方程x2﹣mx+6＝0得到关于m的方程，然后解关于m的方程即可．
解：把x＝3代入方程x2﹣mx+6＝0得9﹣3m+6＝0，
解得m＝5．
故答案是：5．
16．某一时刻，身高1.6m的小明在阳光下的影长是0.6m，同一时刻同一地点测得旗杆的影长是3m，则该旗杆的高度是 　8　m．
【分析】设该旗杆的高度为xm，根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等，即有1.6：0.6＝x：3，然后解方程即可．
解：设该旗杆的高度为xm，
根据题意，得1.6：0.6＝x：3，
解得x＝8．
即该旗杆的高度是8m．
故答案为：8．
17．如图，在一幅长80cm，宽50cm的长方形风景画的四周镶上一条金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是5400cm2，则金色纸边的宽为 　5　cm．

【分析】设金色纸边的宽为xcm，则矩形挂图的长为（80+2x）cm，宽为（50+2x）cm，根据整个挂图的面积是5400cm2，即可得出关于x的一元二次方程，解之取其正值即可得出金色纸边的宽．
解：设金色纸边的宽为xcm，则矩形挂图的长为（80+2x）cm，宽为（50+2x）cm，
依题意得：（80+2x）（50+2x）＝5400，
整理得：x2+65x﹣350＝0，
解得：x1＝5，x2＝﹣70（舍去）．
故答案为：5．
18．如图，四边形ABCD是正方形，AB＝6，E是BC中点，连接DE，DE的垂直平分线分别交AB、DE、CD于M、O、N，连接EN，过E作EF⊥EN交AB于F．下列结论中，正确结论是 　①②④　．（填序号）
①△BEF∽△CNE；②MN＝3；③BF＝AF；④△BEF的周长是12．

【分析】由∠BFE＝∠CEN，∠B＝∠C即可证得△BEF∽△CNE，即可判断①正确；根据三角形面积公式即可判断②正确；求得BF＝4，即可得到BF＝2AF，即可判断③错误；根据勾股定理求得EF，即可求△BEF的周长是12，即可判断④正确；即可求解．
解：∵EF⊥EN，
∴∠BEF+∠CEN＝90°，
∵∠BEF+∠BFE＝90°，
∴∠BFE＝∠CEN，
∵∠B＝∠C，
∴△BEF∽△CNE，故①正确；
∵四边形ABCD是正方形，AB＝6，E是BC中点，
∴CD＝6，CE＝3，
∴DE＝＝＝3，
∵MN垂直平分BE，
∴OD＝OE＝，EN＝DN，
设DN＝x，则EN＝x，CN＝6﹣x，
∵EN2＝EC2+CN2，
∴x2＝32+（6﹣x）2，解得x＝，
∴DN＝，
∵S△DMN＝•DN•AD＝•MN•OD，
∴DN•AD＝MN•OD，即×6＝MN，
∴MN＝3，故②正确；
∵△BEF∽△CNE，
∴，
∵BE＝CE＝3，CN＝6﹣＝，
∴，
∴BF＝4，
∴AF＝6﹣4＝2，
∴BF＝2AF，故③错误；
∵BE＝3，BF＝4，
∴EF＝5，
∴△BEF的周长＝3+4+5＝12，故④正确；
故答案为：①②④．
三、解答题：（本大题共9个小题，共78分解答应写出文字说明、证明过程或演算步骤。）
19．解方程：x2﹣4x＝3．
【分析】在左右两边同时加上一次项系数﹣4的一半的平方，进行配方．
解：由原方程，得
x2﹣4x+4＝3+4，
则（x﹣2）2＝7，
开方，得
x﹣2＝±，
解得x1＝2+，x2＝2﹣．
20．如图，l1∥l2∥l3，AB＝5，DE＝4，EF＝8，求AC的长．

【分析】根据平行线分线段成比例定理列出比例式，把已知数据代入计算，得到答案．
解：∵l1∥l2∥l3，
∴，
即，
∴BC＝10，
∴AC＝AB+BC＝5+10＝15．
21．如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示．
（1）请你通过画图确定灯泡所在的位置．
（2）如果小明的身高AB＝1.6m，他的影子长AC＝1.4m，且他到路灯的距离AD＝2.1m，求灯泡的高．


【分析】（1）连接CB延长CB交DE于O，点O即为所求．连接OG，延长OG交DF于H．线段FH即为所求；
（2）根据＝，构建方程，可得结论．
【解答】（1）解：如图，点O为灯泡所在的位置，
线段FH为小亮在灯光下形成的影子；


（2）解：由已知可得，＝，
∴＝，
∴OD＝4m．
∴灯泡的高为4m．
22．已知：如图，在正方形ABCD中，P是BC上的点，Q是CD上的点，且AQ⊥PQ，△ADQ与△QCP是否相似？并证明你的结论．

【分析】在所要求证的两个三角形中，已知的等量条件为：∠D＝∠C＝90°，若证明两三角形相似，再得出∠DAQ＝∠PQC即可．
解：相似，
证明：∵四边形ABCD是正方形，
∴∠D＝∠C＝90°，
∵AQ⊥PQ，
∴∠DAQ+∠AQD＝90°，∠PQC+∠PQC＝90°，∠AQD+∠PQC＝90°，
∴∠DAQ＝∠PQC，
∴△ADQ∽△QCP．
23．如图，O为原点，B，C两点坐标分别为（3，﹣1）（2，1）．
（1）以O为位似中心在y轴左侧将△OBC放大两倍，并画出图形；
（2）分别写出B，C两点的对应点B′，C′的坐标；
（3）已知M（x，y）为△OBC内部一点，写出M的对应点M′的坐标．

【分析】（1）利用位似变换的性质分别作出B，C的对应点B′，C′即可．
（2）根据B′，C′的位置，写出坐标即可．
（3）探究规律，利用规律解决问题即可．
解：（1）如图，△OB′C′即为所求．
（2）B′（﹣6，2），C′（﹣4，﹣2）．

（3）M′（﹣2x，﹣2y）．
24．汽车产业的发展，有效促进了我国现代化建设，某汽车销售公司2018年盈利1500万元，到2020年盈利2160万元，且从2018年到2020年，每年盈利的年增长率相同．
（1）求每年盈利的年增长率；
（2）若该公司盈利的年增长率继续保特不变，那么2021年该公司盈利能否达到2500万元？
【分析】（1）设每年盈利的年增长率为x，根据题意列出等量关系进行求解即可；
（2）相等关系是：2021年盈利＝2020年盈利×（1+盈利年增长率）．
解：（1）设每年盈利的年增长率为x，
根据题意得：1500（1+x）2＝2160．
解得x1＝0.2，x2＝﹣2.2（不合题意，舍去）．
答：每年盈利的年增长率为20%；

（2）2160（1+0.2）＝2592，2592＞2500
答：2021年该公司盈利能达到2500万元．
25．2019年12月以来，湖北省武汉市部分医院陆续发现不明原因肺炎病例，现已证实该肺炎为一种新型冠状病毒感染的肺炎，其传染性较强．为了有效地避免交叉感染，需要采取以下防护措施：①戴口罩；②勤洗手；③少出门；④重隔离；⑤捂口鼻；⑥谨慎吃．某公司为了解员工对防护措施的了解程度（包括不了解、了解很少、基本了解和很了解），通过网上问卷调查的方式进行了随机抽样调查（每名员工必须且只能选择一项），并将调查结果绘制成如下两幅统计图．

请你根据上面的信息，解答下列问题
（1）本次共调查了　60　名员工，条形统计图中m＝　20　；
（2）若该公司共有员工1000名，请你估计“不了解”防护措施的人数；
（3）在调查中，发现有4名员工对防护措施“很了解”，其中有3名男员工、1名女员工．若准备从他们中随机抽取2名，让其在公司群内普及防护措施，用画树状图或列表法求恰好抽中一男一女的概率（要求画出树状图或列出表格）．
【分析】（1）根据“了解很少”的员工有24名，其所占的百分比为40%，求出总人数即可解决问题；
（2）利用样本估计总体的思想解决问题即可；
（3）根据题意列出图表得出所有等情况数和恰好抽中一男一女的情况数，然后根据概率公式即可得出答案．
解：（1）由统计图可知，“了解很少”的员工有24名，其所占的百分比为40%，
故本次调查的员工人数为24÷40%＝60（名），m＝60﹣12﹣24﹣4＝20．
故答案为：60，20；

（2）根据题意得：
1000×＝200（名），
答：不了解防护措施的人数为200名；

（3）根据题意列表如下：
员工
男甲
男乙
男丙
女
男甲

男乙、男甲
男丙、男甲
女、男甲
男乙
男甲、男乙

男丙、男乙
女、男乙
男丙
男甲、男丙
男乙、男丙

女、男丙
女
男甲、女
男乙、女
男丙、女

共有12种等情况数，其中恰好抽中一男一女的6种，
则恰好抽中一男一女的概率为＝．
26．如图，在Rt△ABC中，AC＝4cm，BC＝3cm，点P由点B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC方向向点C匀速运动，速度为1cm/s，连接PQ．设运动的时间为t（s），其中0＜t＜4．解答下列问题：
（1）AP＝　（5﹣t）cm　，AQ＝　tcm　；（用含t的代数式麦示）
（2）当t为何值时，以P、Q、A为顶点的三角形与△ABC相似？
（3）点P、Q在运动过程中，△APQ能否成为等腰三角形？若能，求出此时t的值；若不存在，请说明理由．


【分析】（1）由勾股定理得AB＝5（cm），再由题意得BP＝tcm，AQ＝tcm，则AP＝AB﹣BP＝（5﹣t）cm；
（2）分两种情况：①△PQA∽△BCA，②△PQA∽△CBA，根据相似三角形的性质列出比例式，代入计算即可；
（3）分三种情况：AP＝AQ，PA＝PQ和QP＝QA，根据等腰三角形的性质，运用相似三角形的性质解答即可．
解：（1）在Rt△ABC中，由勾股定理得：AB＝＝＝5（cm），
由题意得：BP＝tcm，AQ＝tcm，
∴AP＝AB﹣BP＝（5﹣t）cm，
故答案为：（5﹣t）cm，tcm；
（2）分两种情况：
①如图1，当∠PQA＝90°时，△PQA∽△BCA，
则＝，
即＝，
解得：t＝；
②如图2，当∠APQ＝90°时，△PQA∽△CBA，
则＝，
即＝，
解得：t＝；
综上所述，t的值为或时，以P、Q、A为顶点的三角形与△ABC相似；
（3）△APQ能成为等腰三角形，理由如下：
分三种情况：
①如图3，当AP＝AQ时，
5﹣t＝t，
解得：t＝；
②如图4，当AP＝PQ时，过点P作PM⊥AC于M，
则∠AMP＝90°，AM＝QM＝AQ＝，
∵∠ACB＝90°，
∴PM∥BC，
∴△APM∽△ABC，
∴＝，
解得：t＝；
③如图5，当QP＝AQ时，过点Q作QN⊥AB于N，
则∠ANQ＝∠ACB＝90°，AN＝NP＝AP＝（5﹣t），
∵∠NAQ＝∠CAB，
∴△ANQ∽△ACB，
∴＝，
解得：t＝，
综上所述，当t的值为或或时，△APQ能成为等腰三角形．





27．（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝4，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为　BE＝AF　；
（2）【拓展研究】在（1）的条件下，如果正方形CDEF绕点C旋转，当点B，E，F三点共线时，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；
（3）【问题发现】当正方形CDEF旋转到B，E，F三点共线时，求线段AF的长．

【分析】（1）先利用等腰直角三角形的性质得出AD＝，再得出BE＝AB＝4，即可得出结论；
（2）先利用三角函数得出＝，同理得出＝，夹角相等即可得出△ACF∽△BCE，进而得出结论；
（3）分两种情况计算，当点E在线段BF上时，如图2，先利用勾股定理求出EF＝CF＝AD＝2，BF＝2，即可得出BE＝2﹣2，借助（2）得出的结论，当点E在线段BF的延长线上，同前一种情况一样即可得出结论．
解：（1）在Rt△ABC中，AB＝AC＝4，
根据勾股定理得，BC＝AB＝4，
点D为BC的中点，
∴AD＝BC＝2，
∵四边形CDEF是正方形，
∴AF＝EF＝AD＝2，
∵BE＝AB＝4，
∴BE＝AF，
故答案为BE＝AF；

（2）无变化；
如图2，在Rt△ABC中，AB＝AC＝4，
∴∠ABC＝∠ACB＝45°，
∴sin∠ABC＝＝，
在正方形CDEF中，∠FEC＝∠FED＝45°，
在Rt△CEF中，sin∠FEC＝＝，
∴＝，
∵∠FCE＝∠ACB＝45°，
∴∠FCE﹣∠ACE＝∠ACB﹣∠ACE，
∴∠FCA＝∠ECB，
∴△ACF∽△BCE，
∴＝＝，
∴BE＝AF，
∴线段BE与AF的数量关系无变化；

（3）当点E在线段AF上时，如图2，
由（1）知，CF＝EF＝CD＝2，
在Rt△BCF中，CF＝2，BC＝4，
根据勾股定理得，BF＝2，
∴BE＝BF﹣EF＝2﹣2，
由（2）知，BE＝AF，
∴AF＝2﹣2，
当点E在线段BF的延长线上时，如图3，

在Rt△ABC中，AB＝AC＝4，
∴∠ABC＝∠ACB＝45°，
∴sin∠ABC＝＝，
在正方形CDEF中，∠FEC＝∠FED＝45°，
在Rt△CEF中，sin∠FEC＝＝，
∴＝，
∵∠FCE＝∠ACB＝45°，
∴∠FCB+∠ACB＝∠FCB+∠FCE，
∴∠FCA＝∠ECB，
∴△ACF∽△BCE，
∴＝＝，
∴BE＝AF，
由（1）知，CF＝EF＝CD＝2，
在Rt△BCF中，CF＝2，BC＝4，
根据勾股定理得，BF＝2，
∴BE＝BF+EF＝2+2，
由（2）知，BE＝AF，
∴AF＝2+2．
即：当正方形CDEF旋转到B，E，F三点共线时候，线段AF的长为2﹣2或2+2．