初中数学人教版八年级上册14.2 乘法公式综合与测试图片ppt课件

这是一份初中数学人教版八年级上册14.2 乘法公式综合与测试图片ppt课件，共29页。PPT课件主要包含了复习引入，平方差公式，完全平方公式，乘法公式，多项式乘多项式，例题讲解，添括号法则，两个三项式相乘，方法一，方法二等内容，欢迎下载使用。
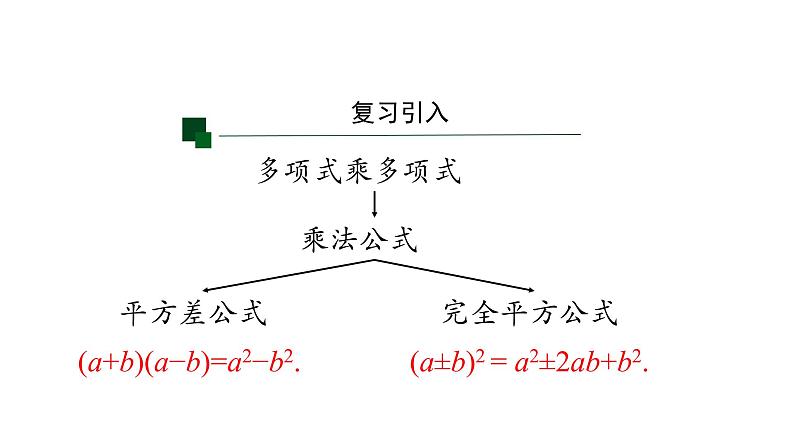
(a+b)(a−b)=a2−b2.
(a±b)2 = a2±2ab+b2.
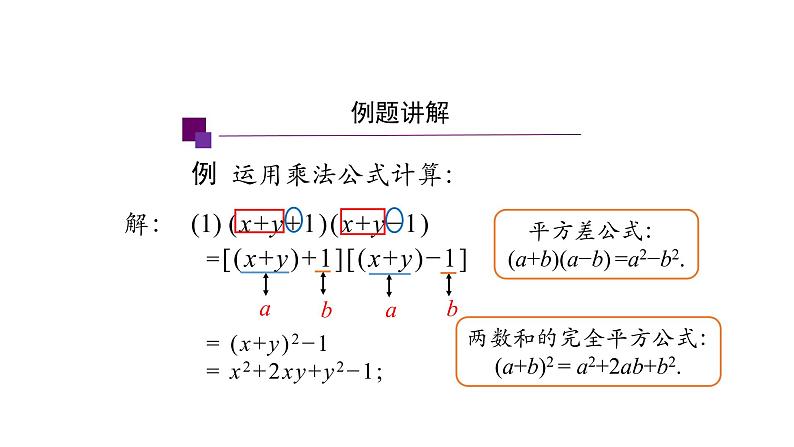
例 运用乘法公式计算： (1) (x+y+1)(x+y−1) ； (2) (x+y−1)(x−y+1) ．
=[(x+y)+1][(x+y)−1]= (x+y)2−1= x2+2xy+y2−1;
例 运用乘法公式计算： (1) (x+y+1)(x+y−1)
平方差公式：(a+b)(a−b) =a2−b2.
两数和的完全平方公式： (a+b)2 = a2+2ab+b2.
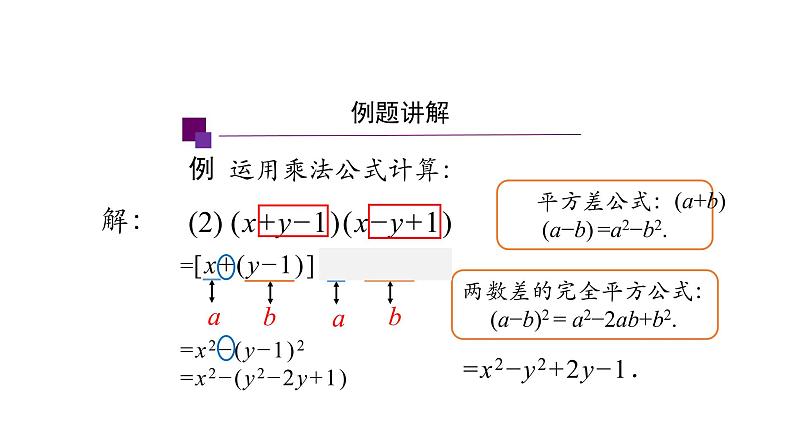
=[x+(y−1)][x−(y−1)]=x2−(y−1)2=x2−(y2−2y+1)
例 运用乘法公式计算： (2) (x+y−1)(x−y+1)
=x2−y2+2y−1．
两数差的完全平方公式： (a−b)2 = a2−2ab+b2.
=[(x+y)+1][(x+y)−1]
例 运用乘法公式计算： (1) (x+y+1)(x+y−1);
=[x+(y−1)][x−(y−1)]
(2) (x+y−1)(x−y+1)．
乘法公式：(a+b)(a−b) =a2−b2；(a±b)2=a2±2ab+b2．
例 运用乘法公式计算： (1) (x+2)(x2+4)(x−2) ；(2) (x+2y)2(x−2y)2；(3) (x+y)2−(x−y)2．
= (x+2)(x−2)(x2+4)= (x2−4)(x2+4)= x4−16 ；
例 运用乘法公式计算： (1) (x+2)(x2+4)(x−2)
乘法交换律： a×b=b×a.
= (x2+4xy+4y2)(x2−4xy+4y2)= (x2+4y2+4xy)(x2+4y2−4xy)
例 运用乘法公式计算： (2) (x+2y)2(x−2y)2
完全平方公式： (a±b)2 = a2±2ab+b2.
= x4−8x2y2+16y4；
= (x2+4y2)2−(4xy)2
= [(x+2y)(x−2y)]2= (x2−4y2)2
逆用积的乘方公式： anbn=(ab)n.
= x4−8x2y2+16y4;
= x2+2xy+y2−(x2−2xy+y2)= x2+2xy+y2−x2+2xy−y2= 4xy.
例 运用乘法公式计算： (3) (x+y)2 −(x−y)2
= [(x+y)+(x−y)][(x+y)−(x−y)]= (x+y+x−y)(x+y−x+y) = 2x·2y = 4xy．
例 运用乘法公式计算： (3) (x+y)2 − (x−y)2
逆用平方差公式：a2−b2=(a+b)(a−b).
例 运用乘法公式计算： (1) (x+2) (x2+4) (x−2)；(2) (x+2y)2(x−2y)2；(3) (x+y)2 − (x−y)2．
例 先化简，再求值：(x+3y)2−(x+3y)(x−3y)，其中x=3，y=−2.
(x+3y)2−(x+3y)(x−3y)= x2+6xy+9y2−(x2−9y2)= x2+6xy+9y2−x2+9y2= 6xy+18y2，
当x=3，y=−2时，原式= 6xy+18y2 = 6×3×(−2)+18×(−2)2 =36.
例 求代数式的值： (1)已知a+b=2，a2−b2=6，求a−b的值；(2)已知x−y=6，xy=−8，求x2＋y2的值.
例 求代数式的值： (1)已知a+b=2，a2−b2=6，求a−b的值；
a+b , a2−b2
(a+b)(a−b) =a2−b2
∵a2−b2=6，(a+b)(a−b) =a2−b2，∴(a+b)(a−b)=6，又∵a+b=2，∴a−b=3；
例 求代数式的值： (2) 已知x−y=6，xy=−8，求x2＋y2的值.
(x−y)2=x2−2xy+y2
x2+y2= (x−y)2+2xy
∵(x−y)2=x2−2xy+y2，∴x2+y2=(x−y)2+2xy，又∵x−y=6，xy=−8，∴x2＋y2=62+2×(−8)=20.
练习 已知(a+b)2=7，(a−b)2=3，求a2+b2的值.
(a+b)2=a2+2ab+b2
(a−b)2=a2−2ab+b2
∵(a+b)2=a2+2ab+b2， (a−b)2=a2−2ab+b2，∴4ab=(a+b)2−(a−b)2，又∵ (a+b)2=7，(a−b)2=3，∴4ab=7−3=4，∴ab=7−3=1，
∵(a+b)2=a2+2ab+b2，∴a2+b2=(a+b)2−2ab =7−2 =5 .
1.乘法公式：（1）平方差公式： (a+b)(a−b)=a2−b2.（2）完全平方公式： (a+b)2=a2+2ab+b2； (a−b)2=a2−2ab+b2.
注意：公式中的a、b可以表示数或式子.
2.平方差公式： (a+b)(a−b)=a2−b2.逆用： a2−b2=(a+b)(a−b).
3.完全平方公式： (a+b)2=a2+2ab+b2； (a−b)2=a2−2ab+b2.常用变形形式： a2+b2=(a+b)2−2ab； a2+b2=(a−b)2+2ab； (a+b)2=(a−b)2+4ab.