人教版九年级上册24.1.1 圆复习课件ppt

这是一份人教版九年级上册24.1.1 圆复习课件ppt，共20页。PPT课件主要包含了解得x5，能力提升，cm≤OP≤5cm，则OD＝5cm，在Rt△OBD中，πcm2，追踪训练等内容，欢迎下载使用。
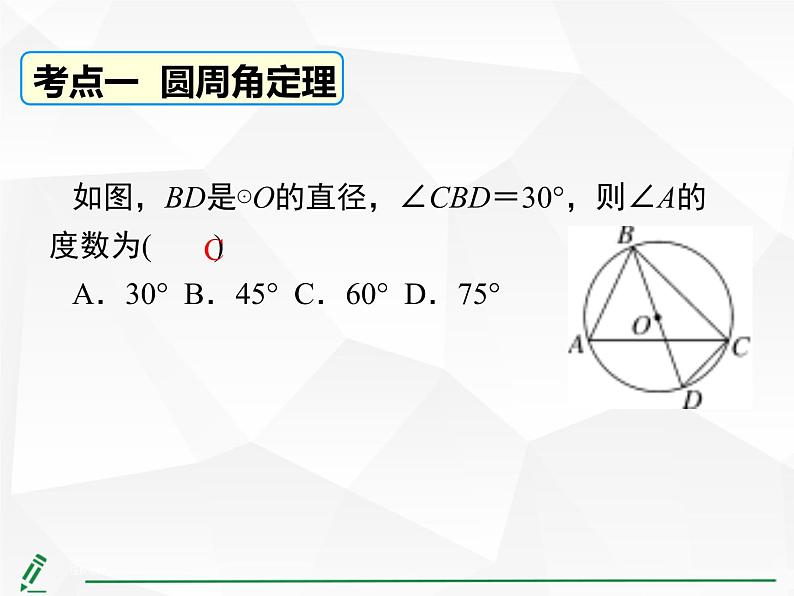
如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为(　　)A．30° B．45° C．60° D．75°
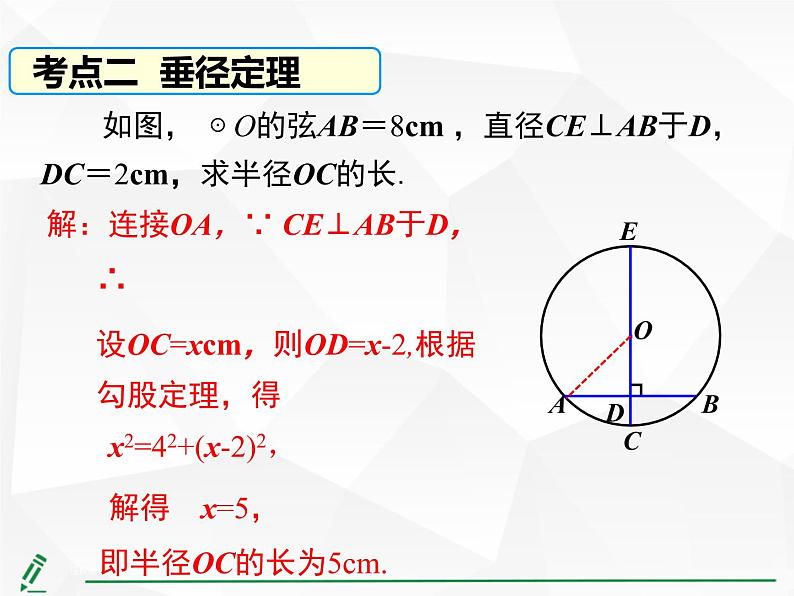
如图， ⊙ O的弦AB＝8cm ，直径CE⊥AB于D，DC＝2cm，求半径OC的长.
解：连接OA，∵ CE⊥AB于D，
设OC=xcm，则OD=x-2,根据勾股定理，得
即半径OC的长为5cm.
x2=42+(x-2)2，
已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.
证明：连接OC(如图). ∵ OA＝OB,CA＝CB, ∴ OC是等腰三角形OAB底边AB上的中线.　 ∴ AB⊥OC. ∵ OC是⊙O的半径, ∴ AB是⊙O的切线.
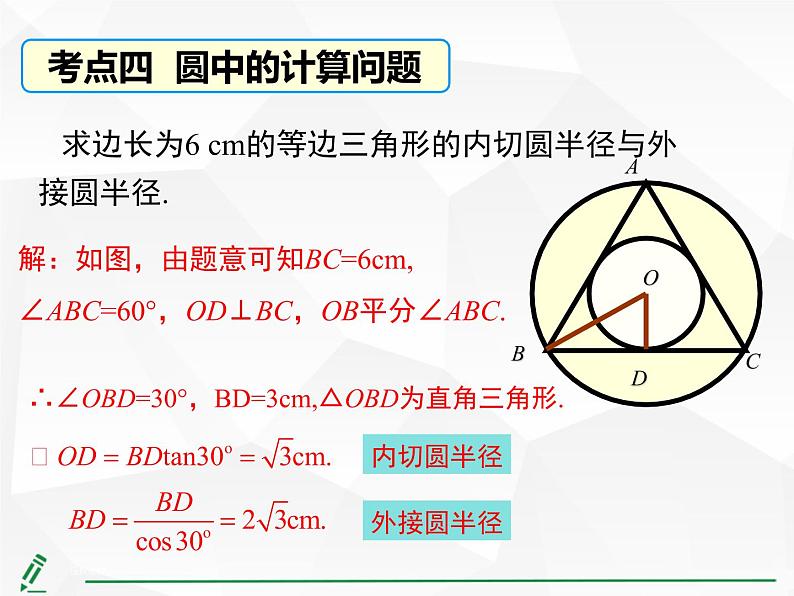
求边长为6 cm的等边三角形的内切圆半径与外接圆半径.
解：如图，由题意可知BC=6cm,∠ABC=60°，OD⊥BC，OB平分∠ABC.
∴∠OBD=30°，BD=3cm,△OBD为直角三角形.
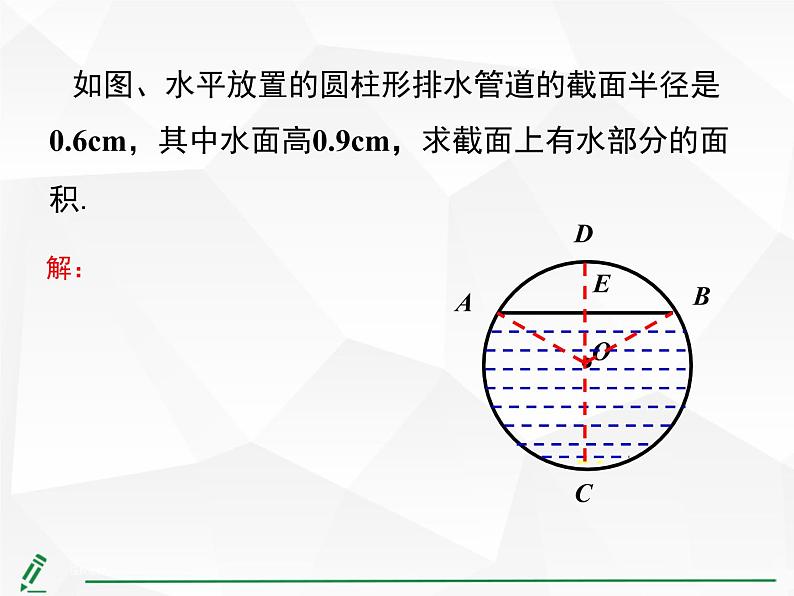
如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.9cm，求截面上有水部分的面积.
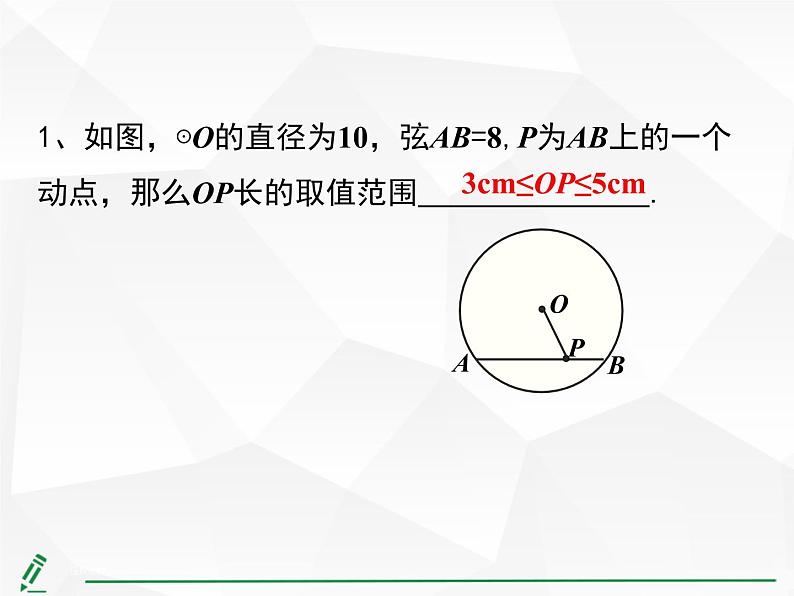
1、如图，⊙O的直径为10，弦AB=8,P为AB上的一个动点，那么OP长的取值范围 .
3、如图，在△ABC中，O是它的外心，BC＝24cm，O到BC的距离是5cm，求△ABC的外接圆的半径．
解：连接OB，过点O作OD⊥BC.
即△ABC的外接圆的半径为13cm.
6.如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．
解：∵正方形的面积等于4，
∴正方形的边长AB=2.
7 .圆锥的底面半径为3cm，母线长为6cm，则这个圆锥侧面展开图扇形的圆心角是_______．8 .一个扇形，半径为30cm，圆心角为120度，用它做成一个圆锥的侧面，那么这个圆锥的底面半径为_____ ．
9. 已知圆锥的底面的半径为3cm，高为4cm，则它的侧面积是 ，全面积是 ．
1.如图，⊙O的直径为10，弦AB=8,P为AB上的一个动点，那么OP长的取值范围 .
3、如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G. 求证：∠FGD＝∠ADC.
证明：∵四边形ACDG内接于⊙O，∴∠FGD＝∠ACD.又∵AB为⊙O的直径，CF⊥AB于E，∴AB垂直平分CD，∴AC＝AD，∴∠ADC＝∠ACD，∴∠FGD＝∠ADC.
方法总结：圆内接四边形的性质是沟通角相等关系的重要依据．
证明：连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP，∴∠B=∠OPB， ∴∠OBP=∠C. ∴OP∥AC. ∵PE⊥AC， ∴PE⊥OP. ∴PE为⊙O的切线.
4.如图,△ABC中，AB=AC，以AB为直径的⊙O交边BC于P， PE⊥AC于E. 求证:PE是⊙O的切线.