北师大版 (2019)必修 第一册3 函数的单调性和最值图片ppt课件

这是一份北师大版 (2019)必修 第一册3 函数的单调性和最值图片ppt课件，共20页。PPT课件主要包含了学习目标，情境导学，新知学习，探究新知，0+∞，奇函数，偶函数，增函数，单调递增，单调递减等内容，欢迎下载使用。

一、幂函数的定义一般地,形如　　　　　(α为常数)的函数,即　　　　是自变量、　　　　是常数的函数称为幂函数. 
名师点析1.幂的指数是一个常数,它可以取任意实数;2.幂值前面的系数是1,否则不是幂函数,如函数y=5 就不是幂函数.3.幂函数的定义域是使xα有意义的所有x的集合,因α的不同,定义域也不同.
二、幂函数的图象和性质1.常见的五种幂函数的图象
可以发现任一幂函数在第一象限内必有图象,在第四象限内无图象.
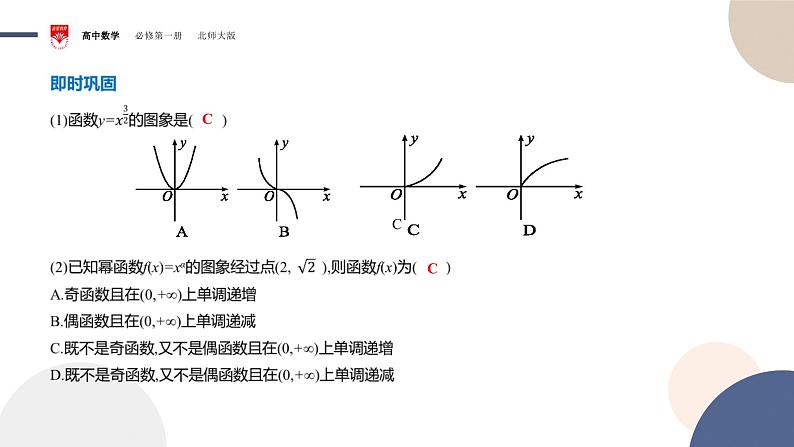
既不是奇函数,也不是偶函数　
名师点析 幂函数y=xα的上述性质可归纳如下:(1)当α>0时,图象都通过点(0,0),(1,1);在第一象限内,函数单调递增.(2)当α<0时,图象都通过点(1,1);在第一象限内,函数单调递减,图象向上与y轴无限接近,向右与x轴无限接近.
即时巩固 判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.(1)幂函数的图象可以出现在平面直角坐标系中的任意一个象限.(　　)(2)幂函数的图象必过(0,0)和(1,1).(　　)
例1 函数f(x)=(m2-m-5)xm-1是幂函数,且当x∈(0,+∞)时,f(x)单调递增,试确定m的值.
解:根据幂函数的定义,得m2-m-5=1,解得m=3或m=-2.当m=3时,f(x)=x2在(0,+∞)上单调递增;当m=-2时,f(x)=x-3在(0,+∞)上单调递减,不符合要求.故m=3.
反思感悟 判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即:(1)系数为1;(2)指数为常数;(3)后面不加任何项.反之,若一个函数为幂函数,则该函数必具有这种形式.
分析:由f(x)=(m2-m-5)xm-1是幂函数,且当x>0时单调递增,可先利用幂函数的定义求出m的值,再利用单调性确定m的值.
解:由幂函数的定义得m2-3m+3=1,解得m=1或m=2;当m=1时,m2-m-2=-2,函数为y=x-2,其图象不过原点,满足条件;当m=2时,m2-m-2=0,函数为y=x0,其图象不过原点,满足条件.综上所述,m=1或m=2.
例2 已知函数y=xa,y=xb,y=xc的图象如图所示,则a,b,c的大小关系为(　　)A.c分析:利用幂函数在第一象限内的图象特征和性质,结合所给图象分析并判断a,b,c的大小关系.
解析:由幂函数的图象特征,知c<0,a>1,0变式训练 如图所示,曲线C1与C2分别是函数y=xm和y=xn在第一象限内的图象,则下列结论正确的是(　　)A.nm>0D.m>n>0
解析:画出直线y=x0的图象,作出直线x=2,与三个函数图象交于点(2,20),(2,2m),(2,2n).由三个点的位置关系可知,n利用幂函数的单调性比较大小
反思感悟 1.比较幂大小的三种常用方法
2.利用幂函数单调性比较大小时要注意的问题比较大小的两个实数必须在同一函数的同一个单调区间内,否则无法比较大小.
分析:先利用幂函数的定义求出f(x),g(x)的解析式,再利用图象判断.
变式训练 已知(0.71.3)m<(1.30.7)m,求m的取值范围.
解:根据幂函数y=x1.3的图象,知当01时,y>1,∴1.30.7>1.于是有0.71.3<对于幂函数y=xm,由(0.71.3)m<(1.30.7)m知,当x>0时,随着x的增大,函数值y也增大,所以m>0.
3.幂函数f(x)=x3m-5(m∈N)在区间(0,+∞)上是单调递减,且对定义域中的任意x,有f(-x)=f(x),则m等于(　　)A.0B.1C.2D.3