浙教版初中数学八年级上册第三次月考快速提分卷 （1-4章）

这是一份浙教版初中数学八年级上册第三次月考快速提分卷 （1-4章），共9页。试卷主要包含了单选题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。
 浙教版初中数学八年级上册第三次月考快速提分卷（1-4章）考试时间：120分钟 满分：120分

姓名：__________ 班级：__________考号：__________一、单选题（共10题；共30分）1. ( 3分 ) 如图，直线y x+3分别与x轴，y轴交于点A、点B  ， 抛物线y=x2+2x﹣2与y轴交于点C  ， 点E在抛物线y=x2+2x﹣2的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（   ）  A. 4    B. 4.6      C. 5.2    D. 5.62. ( 3分 ) 如图，在 △ABC中，CD是AB边上的高，BE平分∠ABC交CD于点E，若BC=8，DE=4， 则△BCE的面积为（   ） A. 32    B. 16       C. 8     D. 43. ( 3分 ) 如图，点 是矩形 的中心， 是 上的点，沿 折叠后，点 恰好与点 重合，若 ，则折痕 的长为（    ）  A.        B.         C.           D. 4. ( 3分 ) 如图，△ABC是一张顶角为120°的三角形纸片，AB＝AC，BC＝6，现将△ABC折叠，使点B与点A 重合，折痕为DE，则DE的长为（  ）  A. 1         B. 2        C. 2          D. 35. ( 3分 ) 如图，在△ABC中，AB=AC=13，BC=10，点D为BC的中点，DE⊥AB，垂足为点E，则DE等于（   ）  A.       B.           C.         D. 6. ( 3分 ) 下列命题.假命题是（　　）            A. 如果两条直线都与第三条直线平行，那么这两条直线也互相平行
B. 在同一平面内，过一点有且只有一条直线与已知直线垂直
C. 两条直线被第三条直线所截，同旁内角互补
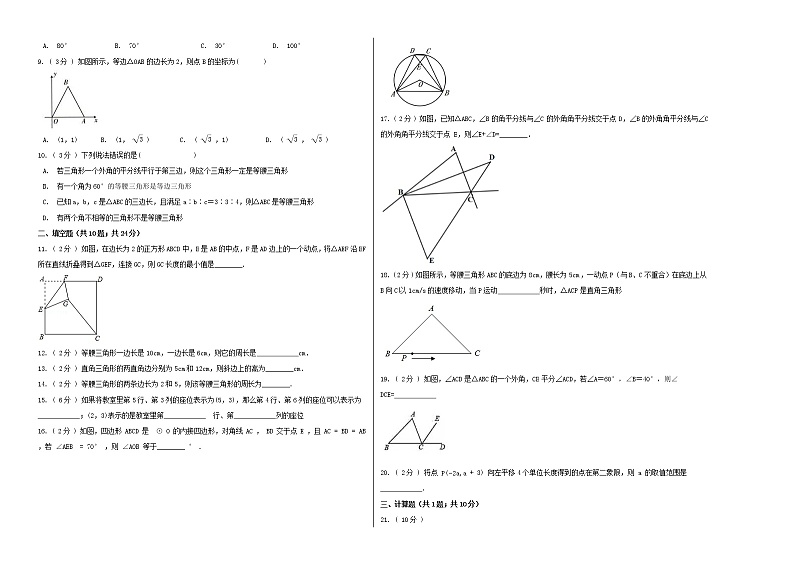
D. 两直线平行，内错角相等7. ( 3分 ) 如图，AD∥BE  ， AC与BC相交于点C  ， 且∠1＝ ∠DAB  ， ∠2＝ ∠EBA ． 若∠C＝45°，则n＝（    ） A. 2         B. 3        C. 4     D. 58. ( 3分 ) 如图所示， ， ， ， ，则 等于（  ）  A.       B.         C.       D. 9. ( 3分 ) 如图所示，等边△OAB的边长为2，则点B的坐标为(    ) A. (1，1)   B. (1， )    C. ( ，1)     D. ( ， )10. ( 3分 ) 下列说法错误的是(        )            A. 若三角形一个外角的平分线平行于第三边，则这个三角形一定是等腰三角形
B. 有一个角为60°的等腰三角形是等边三角形
C. 已知a，b，c是△ABC的三边长，且满足a∶b∶c＝3∶3∶4，则△ABC是等腰三角形
D. 有两个角不相等的三角形不是等腰三角形二、填空题（共10题；共24分）11. ( 2分 ) 如图，在边长为2的正方形ABCD中，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF所在直线折叠得到△GEF，连接GC，则GC长度的最小值是________. 12. ( 2分 ) 等腰三角形一边长是10cm，一边长是6cm，则它的周长是      cm．    13. ( 2分 ) 直角三角形的两直角边分别为5cm和12cm，则斜边上的高为________cm．    14. ( 2分 ) 等腰三角形的两条边长为2和5，则该等腰三角形的周长为________.    15. ( 6分 ) 如果将教室里第5行、第3列的座位表示为(5，3)，那么第4行、第6列的座位可以表示为      ；(2，3)表示的是教室里第       行、第      列的座位    16. ( 2分 ) 如图，四边形 是 的内接四边形，对角线 ， 交于点 ，且 ，若 ，则 等于________ .  17. ( 2分 ) 如图，已知△ABC，∠B 的角平分线与∠C 的外角角平分线交于点 D，∠B 的外角角平分线与∠C 的外角角平分线交于点 E，则∠E+∠D=________．  18. ( 2分 ) 如图所示，等腰三角形ABC的底边为8cm，腰长为5cm ，一动点P（与B、C不重合）在底边上从B向C以1cm/s的速度移动，当P运动      秒时，△ACP是直角三角形  19. ( 2分 ) 如图，∠ACD是△ABC的一个外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠DCE=       20. ( 2分 ) 将点 向左平移4个单位长度得到的点在第二象限，则 的取值范围是      .    三、计算题（共1题；共10分）21. ( 10分 )       （1）解方程： ．    （2）解不等式组： ．    四、作图题（共1题；共10分）22. ( 10分 ) 如图，△ABC的顶点坐标分别为A（-2,1），B（-3,-2），C（1，-2）.把△ABC向上平移4个单位长度，再向右平移3个单位长度，得到△A′B′C′.  （1）在图中画出△A′B′C′，并写出点A′，B′，C′的坐标；    （2）连接A′C和A′A，求三角形AA′C的面积.    五、解答题（共3题；共46分）23. ( 15分 ) 如图所示，在操场上竖直立着一根长为2米的测影竿CD，早晨测得它的影长AD为4米，中午测得它的影长BD为1米，试判定△ABC的形状，并说明理由。 24. ( 15分 ) 如图，▱ABCD中，AC为对角线，G为CD的中点，连接AG并廷长交BC的延长线于点F，连接DF，求证：四边形ACFD为平行四边形. 25. ( 16分 ) 如图，四边形ABCD中，∠B=90°，AB=6，BC=8，CD=24，AD=26，求四边形ABCD的面积． 
答案解析部分一、单选题1.【答案】 C   【解析】∵y=x2+2x﹣2的对称轴为 ，C(0，﹣2)， ∴C点关于对称轴对称的点C'(﹣2，﹣2)，过点C'作直线AB的垂线，交对称轴与点E  ， 交直线AB于点F  ， ∴CE=C'E  ， 则C'F=CE+EF=C'E+EF是CE+EF的最小值；∵直线y x+3，设直线C'F的解析式为 ，将C'(﹣2，﹣2)代入得： ，解得： ，∴C'F的解析式为y x ，解方程组 ，得： ，∴F( ， )，∴C'F ．2.【答案】 B   【解析】解：过点E作EF⊥BC于点F，

∵CD是AB边上的高，BE平分∠ABC，
∴CD⊥BC，
∴ED=EF=4
∴S△BCE=.
3.【答案】     A【解析】解：由题意可知： ， ， 在 中， 设 ，则 ， 在 中， ，即 解得 ，即 在 中， 4.【答案】 A   【解析】解：作AH⊥BC于H， ∵AB＝AC，AH⊥BC，∴BH＝ BC＝3，∵∠BAC＝120°，AB＝AC，∴∠B＝30°，∴AB＝ ，由翻折变换的性质可知，DB＝DA＝ ，∴DE＝BD·tan30°＝1，5.【答案】 D   【解析】连接AD， ∵△ABC中，AB=AC=13，BC=10，D为BC中点，∴AD⊥BC，BD= BC=5，∴AD= =12，又∵DE⊥AB，∴ BD•AD= AB•ED，∴ .6.【答案】 C   【解析】解：∵如果两条直线都与第三条直线平行，那么这两条直线也互相平行， ∴选项A是真命题；∵在同一平面内，过一点有且只有一条直线与已知直线垂直，∴选项B是真命题；∵两条直线被第三条直线所截，同旁内角不一定互补，∴选项C是假命题；∵两直线平行，内错角相等，∴选项D是真命题.7.【答案】     C【解析】解：过C作CF∥AD，

∴∠1=∠ACF，
∵AD∥BE，
∴CF∥BE，
∠2=∠BCF，
∴∠1+∠2=∠ACF+∠BCF=∠ACB=45°，
∴∠1+∠2=   ∠DAB +   ∠EBA ，
∵AD∥BE，
∴∠DAB+∠EBA=180°，
∴∠1+∠2=（∠DAB+∠EBA）=×180°=45° ，
∴n=4，
8.【答案】 A   【解析】 ， ，即 ，在 和 中， ， ， ， ，9.【答案】     B【解析】解：过点B作BD⊥x轴于点D，
∵△ABO是等边三角形，AO=2
∴OD=1，  ，
∴点B的坐标(1， ).
10.【答案】 D   【解析】解：A、若三角形一个外角的平分线平行于第三边，则这个三角形一定是等腰三角形，正确；
B、有一个角为60°的等腰三角形是等边三角形，正确；
C、已知a，b，c是△ABC的三边长，且满足a∶b∶c＝3∶3∶4，则△ABC是等腰三角形，正确； D、有两个角不相等的三角形有可能是等腰三角形，错误；二、填空题11.【答案】 ﹣1   【解析】解：如图，当点G在CE上时，此时CG的值最小， ∵将△AEF沿EF所在直线折叠得到△GEF，∴AE=GE，∵E是AB边的中点，AB=2，∴AE=BE=GE=1，∵BC=AB=2，∴CE= = = ∴GC=CE-GE= -1.12.【答案】 26或22   【解析】解：若6cm为等腰三角形的腰长，则10cm为底边的长， 6cm，6cm，10cm可以构成三角形，此时等腰三角形的周长=6+6+10=22（cm）；若10cm为等腰三角形的腰长，则6cm为底边的长，10cm，10cm，6cm可以构成三角形，此时等腰三角形的周长=10+6+10=26（cm）；则等腰三角形的周长为26cm或22cm．13.【答案】 ．   【解析】解：∵直角三角形的两条直角边分别为5cm，12cm， ∴斜边为： ＝13cm，设斜边上的高为h，则直角三角形的面积为 ×5×12＝ ×13•h，∴h＝ cm，14.【答案】 12   【解析】解：当5为底时，其它两边都为2， ∵2+2＜5，∴不能构成三角形，故舍去，当5为腰时，其它两边为2和5，5，5，2可以构成三角形，∴周长为5+5+2=12.15.【答案】 (4，6)；2；3   【解析】解：第4行，第6列的座位表示为（4,6）；（2,3）表示的为教室第2行，第3列。
根据教室中数对的表示方法，得到数对的含义。16.【答案】 125   【解析】解：根据题意， ∵在圆中，有 ，∴ ，∴ ，∴ ，在△ABE中， ，∴ ，在等腰△ABC中， 则 ，∴ ；17.【答案】 90°   【解析】解：∵BD，BE分别是∠B的角平分线和外角平分线， ∴∠DBE= ×180°=90°，∴∠D+∠E=180°-∠DBE=180°-90°=90°．18.【答案】 1.75或4   【解析】解：如图，作AD⊥BC， ∵AB=AC=5cm，BC=8cm，∴BD=CD=4cm，当点P运动到与点D重合时， 是直角三角形，此时BP=4，∴运动时间为4÷1=4（秒）；当∠PAC=90°时，设PD=x∴ ，又∵ ，∴ ，∴ ，∴BP=4－2.25=1.75，所以运动时间为1.75÷1=1.75（秒）；综上可得：当P运动4秒或1.75秒时， 是直角三角形；19.【答案】 50°   【解析】解：∵∠ACD是△ABC的一个外角，
∴∠ACD=∠A+∠B=60°+40°=100°，
∵CE平分∠ACD，
∴∠DCE=∠ACD=×100°=50°.
20.【答案】    【解析】解：点 向左平移4个单位长度后的点的坐标为 . 因为平移后的点位于第二象限，所以点的横坐标小于0，纵坐标大于0，所以 解得 所以 .三、计算题21.【答案】 （1）解：分式方程变形得： ，  去分母得： ，解得： ，检验：把 代入得： ，则分式方程的解为 ；
（2）解： ，  由①得： ，由②得： ，∴不等式组的解集为 ．【解析】（1）解分式方程的步骤：①去分母：方程两边同乘最简公分母，约去分母，化为整式方程；
②求解：求出整式方程的解；
③验根：把整式方程的解代入最简公分母，结果为0，是分式方程的增根，分式方程无解，结果不为0，是分式方程的解；
（2）一元一次不等式组的解法步骤：①分别求出不等式组中各个不等式的解集；
②根据口诀“同大取大，同小取小，大小小大中间找，大大小小无解了”找出它们的公共部分即可.  四、作图题22.【答案】 （1）解：平移得到△ 如图所示   ∵A（-2,1），B（-3,-2），C（1，-2）∴A′（1,5），B′（0,2），C′（4,2）
（2）解：∵A′（1,5），C（1，-2），A（-2,1） ∴S三角形AA’C= ×7×3= 【解析】（1）首先确定A、B、C三点向上平移4个单位长度，再向右平移3个单位长度后对应点的位置，再连接即可，然后再根据纵坐标加4，纵坐标加3，写出坐标即可；
（2）利用三角形的面积公式计算即可.五、解答题23.【答案】     解：△ABC是直角三角形．理由如下： 由题意，得CD⊥AB，CD=2，AD=4，BD=1，所以BC2= BD2 +CD2=5，AC2=AD2 +CD2 =20，AB2=25，所以BC2 +AC2=AB2 ，所以△ABC是直角三角形．【解析】先求出 BC2 +AC2=AB2   ，  再证明直角三角形即可。24.【答案】 证明：∵在▱ABCD中，AD∥BF. ∴∠ADC=∠FCD.∵G为CD的中点，∴DG=CG.在△ADG和△FCG中， ，∴△ADG≌△FCG（ASA）∴AD=FC.又∵AD∥FC，∴四边形ACFD是平行四边形.【解析】由平行四边形的对边平行得 AD∥BF ，根据二直线平行，内错角相等证出∠ADC=∠FCD，然后利用ASA证明△ADG≌△FCG可得AD=FC，根据一组对边平行且相等的四边形是平行四边形可得结论.25.【答案】 解：连结AC，  在△ABC中，∵∠B=90°，AB=6，BC=8，∴AC= =10，S△ABC= AB•BC= ×6×8=24，在△ACD中，∵CD=24，AD=26，AC=10，∴CD2+AC2=AD2  ， ∴△ACD是直角三角形，∴S△ACD= AC•CD= ×10×24=120． ∴四边形ABCD的面积=S△ABC+S△ACD=24+120=144．【解析】连接AC，根据勾股定理求出AC，根据勾股定理的逆定理求出△ACD是直角三角形，分别求出△ABC和△ACD的面积，即可得出答案．