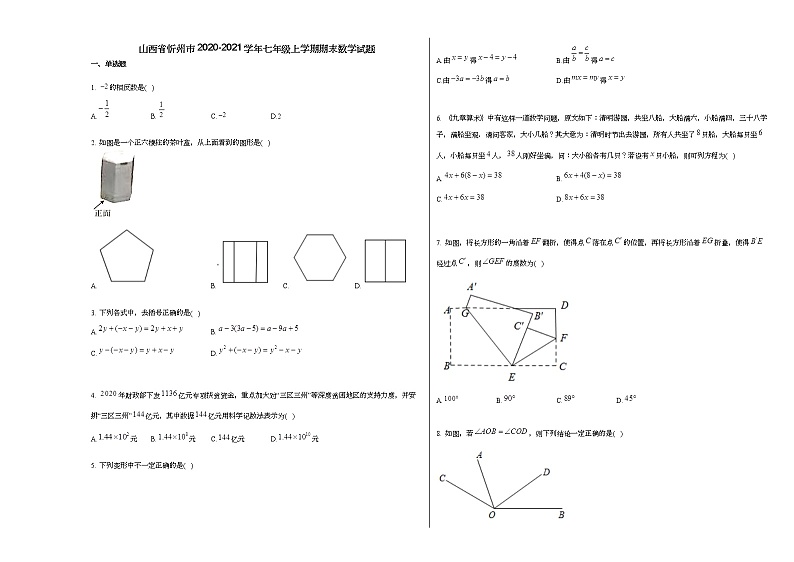
山西省忻州市2020-2021学年七年级上学期期末数学试题新人教版

这是一份山西省忻州市2020-2021学年七年级上学期期末数学试题新人教版，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


1. 的相反数是( )
A.B.C.D.2

2. 如图是一个正六棱柱的茶叶盒，从上面看到的图形是( )

A.B.C.D.

3. 下列各式中，去括号正确的是( )
A.B.
C.D.

4. 年财政部下发亿元专项扶贫资金，重点加大对“三区三州”等深度贫困地区的支持力度，并安排“三区三州”亿元，其中数据亿元用科学记数法表示为( )
A.元B.元C.亿元D.元

5. 下列变形中不一定正确的是( )
A.由得B.由得
C.由得D.由得

6. 《九章算术》中有这样一道数学问题，原文如下：清明游园，共坐八船，大船满六，小船满四，三十八学子，满船坐观．请问客家，大小几船？其大意为：清明时节出去游园，所有人共坐了只船，大船每只坐人，小船每只坐人，人刚好坐满，问：大小船各有几只？若设有只小船，则可列方程为( )
A.B.
C.D.

7. 如图，将长方形的一角沿着翻折，使得点落在点的位置，再将长方形沿着折叠，使得经过点，则的度数为( )

A.B.C.D.

8. 如图，若，则下列结论一定正确的是( )

A.B.
C.D.

9. 下列说法：①倒数等于它本身的数为，；②单项式的次数是；③同角的补角相等；④连接两点的线段就是两点之间的距离，其中正确的个数有( )
A.个B.个C.个D.个

10. 观察下列算式：
第个：，
第个：，
第个：，
……
根据你观察到的规律，则第个算式应表示为( )
A.B.
C.D.
二、填空题

计算：________．

如图，从地到地有三条道路(①,②,③)，其中最短的道路是________．


有三个连续的奇数，中间的一个是，则这三个数的和为________.

从年开始，每年的月被定为我国的“全民阅读月”，小第月我们迎来了第个全民阅读月．某书店将进价为元/套的书籍，标价元/套出售，“全民阅读月”期间打折销售，仍可获利，则的值为________．

线段的长度为，点为直线上一点，且，点为的中点，则线段的长度为________．
三、解答题

计算
（1）；

（2）．

解方程：
（1）；

（2）．

先化简，再求值：，其中．

太原地铁号线，是太原市和山西省开工建设的第一条地铁线路，是贯穿太原市南北交通大动脉，号线一期工程南起西桥站，北至尖草坪站，大致可看作是在南北方向直线上的线路，共设个站点．其中部分站点如图所示．某天，小张从北大门站乘坐地铁出发，始终在该线的站点做志愿服务工作，在站下车时，本次志愿服务工作结束．若规定向南为正，则小张当天的乘车记录如下：，，，，．（单位：站）

（1）通过计算确定小张下车的站是哪个站点？

（2）若假设相邻两个站之间的距离均为千米，求这天小张乘坐地铁的总路程．

阅读材料，完成任务．
七年级同学在学完解一元一次方程后，已掌握了一元一次方程的一般解法，有同学发现在一元一次方程的部分习题和练习题中，存在着许多解题技巧，只要在解题中注重研究其结构特点和特殊规律，巧妙地运用某些基本性质、法则，就可以达成“一点通”的效果．小明是一名喜欢动脑筋的学生，在解方程时，不是直接给方程去括号，而是假设，然后把方程变形为：
，
，
．
，
解，得．
上面的问题中利用新的未知量来代替原来的未知量，求出新的未知量后，再利用其替代原来的未知量，从而得以求解，这种解方程的方法叫做换元法．
任务：参照材料中的解题方法解方程．

公租房作为一种保障性住房，租金低、设施全受到很多家庭的欢迎．某市为解决市民的住房问题，专门设计了如图所示的一种户型，并为每户卧室铺了木地板，其余部分铺了瓷砖．

（1）木地板和瓷砖各需要铺多少平方米？

（2）若，，地砖的价格为元/平方米，木地板的价格为元/平方米，则每套公租房铺地面所需费用为多少元？

如图，若，射线在的内部，射线，分别是，的平分线．

（1）当时，________；

（2）当为的平分线时，________；

（3）当射线在内部转动（不与边，重合），求的度数．

为了响应节约用电的号召，提高人们的节约用电意识，某市对居民生活用电采取阶梯电价来计费，电费价格如表：
例如：某户居民月份用电量为度，则应缴电费为：（元）．
（1）若某户居民月份用电量为度，则应缴电费为________元；

（2）若某户居民月共电费为元，则该户居民的用电量为多少度？
参考答案与试题解析
山西省忻州市2020-2021学年七年级上学期期末数学试题
一、单选题
1.
【答案】
D
【考点】
相反数
有理数的加法
轴对称图形
【解析】
根据相反数的定义进行求解即可．
【解答】
解：−2的相反数是2．
故选D．
2.
【答案】
C
【考点】
由三视图判断几何体
认识立体图形
轴对称图形
【解析】
根据正六棱柱的俯视图为正六边形，即可得出结论．
【解答】
一个正六棱柱的茶叶盒，从上面看到的图形是：正六边形，
故选C．
3.
【答案】
D
【考点】
去括号与添括号
有理数的乘方
合并同类项
【解析】
根据去括号法则，逐一判断选项，即可得到答案．
【解答】
A．2y+−x−y=2y−x−y，故该选项错误，
B．a−33a−5=a−9a+15，故该选项错误，
C．y−−x−y=y+x+y，故该选项错误，
D．y2+−x−y=y2−x−y，故该选项正确，
故选D．
4.
【答案】
D
【考点】
科学记数法--表示较大的数
科学记数法--表示较小的数
三角形三边关系
【解析】
根据科学记数法的定义，即可得到答案．
【解答】
144亿元=1.44×1020元，
故选D．
5.
【答案】
D
【考点】
等式的性质
【解析】
直接利用等式的基本性质逐一判断选项，即可得到答案．
【解答】
A．由x=y得x−4=y−4，正确，不符合题意，
B．由ab=cb得a=c，正确，不符合题意，
C．由−3a=−3b得a=b，正确，不符合题意，
D．由mx=my且m≠0，得x=y，故原选项错误，符合题意．
故选D．
6.
【答案】
A
【考点】
由实际问题抽象出一元一次方程
等腰三角形的判定与性质
由实际问题抽象出一元二次方程
【解析】
一共是38人，设小船有x条，那么大船就有8−x条，用x分别表示出大船和小船坐的人数，进而列方程，即可求解．
【解答】
解：设小船有x条，那么大船就有8−x条，
由题意得：4x+68−x=38
故选A．
7.
【答案】
B
【考点】
翻折变换（折叠问题）
矩形的性质
勾股定理
【解析】
由折叠的性质可得∠GEB=∠GEB′=12∠BEB′∠CEF=∠FEC′=12∠CEB′，由∠BEB′+∠CEB′=180∘可求解2GE
【解答】
解：由题意及折叠的性质可得：∠GEB=∠GEB′=12∠BEB′∠CEF=∠FEC′=12∠CEB′
∠BEB′+∠CEB′=180∘
．∠GEF=∠GE′+∠FEB′=12(∠BEB′+∠CE′)′)=90∘
故选B．
8.
【答案】
C
【考点】
有理数大小比较
有理数的乘方
平行线的判定与性质
【解析】
根据角的和差关系，直接得到答案，即可．
【解答】
∠AOB=∠COD
∠AOB−∠AOD=∠COD−∠AOD，即：∠AOC=∠BOD
故选C．
9.
【答案】
A
【考点】
余角和补角
互余两角三角函数的关系
两点间的距离
倒数
同角三角函数的关系
【解析】
根据倒数，单项式的次数，补角的性质，两点间的距离定义，逐一判断，即可得到答案．
【解答】
解：①倒数等于它本身的数为±1，故原说法错误；
②单项式2mn3的次数是6，故原说法错误；
③同角的补角相等，故原说法正确；
④连接两点的线段的长度是两点之间的距离，故原说法错误；
…正确的个数有1个，
故选A．
10.
【答案】
B
【考点】
规律型：数字的变化类
【解析】
根据等式的变化规律，直接写出答案，即可．
【解答】
由等式的规律可知：等式的左边是相邻自然数的平方差，等式右边是负奇数，
则第几个算式应表示为：n2−n+12=−2n−1
故选B．
二、填空题
【答案】
加加−827
【考点】
有理数的混合运算
有理数的减法
多边形内角与外角
【解析】
根据有理数的乘方运算，直接求解，即可．
【解答】
−233=−827
故答案是：−827
【答案】
②
【考点】
线段的性质：两点之间线段最短
【解析】
根据两点之间线段最短即可解答．
【解答】
从A到B有三条道路，选择道路②最短，理由是：两点之间线段最短．
故答案为：②．
【答案】
6n+3
【考点】
列代数式
【解析】
三个连续的奇数，它们之间相隔的数为，分别表示这三个奇数，列式化简即可．
【解答】
中间的一个是2n+1
第一个为2n−1，最后一个为2n+3，则
三个数的和为(2n−1+2n+1+2n+3=6n+3
故答案为6n+3
【答案】
8
【考点】
一元二次方程的应用
一元一次方程的应用——工程进度问题
一元一次方程的应用——打折销售问题
【解析】
根据全民阅读月“期间打》折销售，仍可获利20%，列出方程，即可求解．
【解答】
由题意得：180⋅x10−120=120×20%，解得：x=8
故答案是：8．
【答案】
9cm或11cm
【考点】
两点间的距离
线段的中点
线段的和差
【解析】
由题意易得BC=2cm，然后分点C在线段AB上和点C在线段AB的延长线上，进而根据线段的和差关系可求解．
【解答】
解：AB=10cmBC=15⋅AB
.BC=2cm
点E为BC的中点，
…BE=12BC=1cm
①当点C在线段AB上，如图所示：
ACEB
则有：AE=AB−BE=9cm
②当点C在线段AB的延长线上，如图所示：
ABEC
则有：AE=AB+BE=1cm
综上所述：线段AE的长度为9cm或11cm；
故答案为9cm或11cm．
三、解答题
【答案】
（1）−1:．；
（2）22
【考点】
有理数的混合运算
有理数的减法
轴对称图形
【解析】
（1）先算乘方，然后再进行有理数的加减运算；
（2）利用乘法分配律进行有理数的混合运算即可．
【解答】
（1）原式=−5−8−2=−15
（2）原式=59×36−13×36+718×36=20−12+14=22
【答案】
（1）x=92；
（2）x=−115
【考点】
解一元一次方程
【解析】
（1）方程去括号，移项合并，把x系数化为1，即可求出解；
（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
【解答】
（1）2x−5x−4=x+2
去括号得：2x−5x−20=x+2
移项合并得：−4x=−18
系数化为1得：x=92
（2）1−3x+17=1−2x3
两边同乘以21，去分母得：21−33x+1=71−2x
去括号得：21−9.x−3=7−14
移项合并得：5x=−11
系数化为1得：x=−115
【答案】
−4a2−3a−2,−24
【考点】
整式的加减——化简求值
【解析】
利用去括号，合并同类项法则，先化简，再代入求值，即可．
【解答】
原式=2a2+3a−2−6a2−6a
=−4a2−3a−2
当a=2时，原式=−4×22−3×2−2=−24
【答案】
（1）胜利街站；
（2）16.5千米
【考点】
规律型：图形的变化类
一次函数的应用
解直角三角形的应用-方向角问题
【解析】
（1）把乘车记录相加，再根据结果是负数，即可得到答案；
（2）把乘车记录的绝对值相加，再把所得的结果×1.5，即可求解．
【解答】
（1）+2−|−3+5−4=−1
．A点为北大门站往北1站，即胜利街站；
（2）|+2|+|−1|+|−3|+|+5|+|−4|=15（站），
15×1=16.5（千米），
答：这天小张乘坐地铁的总路程为16.5千米．
【答案】
[加加加=−−4
【考点】
解一元一次方程
【解析】
根据题示的方法，设7−2x=，将原方程转化为关于a的方程求解即可．
【解答】
解：7−2x3=27−2x5−1
设7−2x=，则原方程变形为：
a3=2a5−1
…115a=1
解得，a=15
即7−2x=15
解得，x=−4
【答案】
（1）10uab，15ab；
（2）每套公租房铺地面所需费用为10500元．
【考点】
列代数式求值
【解析】
（1）根据长方形的面积公式，用代数式直接表示即可；
（2）分别求出木地板和瓷砖的费用，再相加，即可求解．
【解答】
（1）木地板面积=5b−b−2b×2a+5a−2a×2b
=2b×2a+3a×2b
=10ab（平方米），
瓷砖面积=5a×5b−10b=15ab（平方米），
（2）当a=1.5b=2时，10ab=10×1.5×2=30（平方米），
30×200=6000（元），
15ab=15×1.5×2=45（平方米），
45×100=4500（元），
4500+6000=10500（元），
答：每套公租房铺地面所需费用为10500元．
【答案】
（1）60；
（2）60;．
（3）60∘
【考点】
角平分线的性质
【解析】
（1）根据角平分线的定义和角的和差即可得到结论；
（2）根据角平分线的定义和角的和差即可得到结论；
（3）根据角平分线的定义和角的和差即可得到结论．
【解答】
（1）∶OM，ON分别是∠AOC和∠BOC的角平分线，
小20M=12∠AOC=20∘2CON=12∠BOC=12∠AOB−∠AOC=12120∘−40∘=40∘
∴ ∠MON=∠MOC+∠NOC=60∘
故答案为：60；
（2）：OC为∠AOB的平分线，
△AOC=∠BOC=12∠AOB=60∘
OM，ON分别是∠AOC和∠BOC的角平分线，
2COM=12∠AOC=30∘2CON=12∠BOC=30∘
∴ ∠MON=∠MOC+∠NOC=60∘
故答案为：60；
（3）射线OMON分别是∠AOC∠BOC的平分线，
小2COM=12∠AOC,OC,N=12∠BOC
．∠MON=∠COM+∠CON=12∠AOC+12∠BOC=12∠AOC+∠BOC=12∠AOB=60∘
【答案】
（1）129；
（2）12月该户居民的用电量为291度
【考点】
一元一次方程的应用——其他问题
一元二次方程的应用
多边形内角与外角
【解析】
（1）根据题意，列出算式，即可求解；
（2）先判断12月份用电量超过260度，设12月该户居民的用电量为x度，列出方程即可求解．
【解答】
（1）由题意得：170×0.5+250−17×0.5+0.05=129（元），
故答案是：129；
（2）170×0.5+260−170×0.5+0.05=134.5（元），159.3>134.5
设12月该户居民的用电量为x度x>260
由题意得：170×0.5+260−170×0.5+0.05+x−260×0.5+0.3=159.3
解得：x=29
答：12月该户居民的用电量为291度．类别
分档电量（度/户·月）
电价标准（元/度）
一档
不超过度/户·月
二档
超过度/户·月，但不超过度/户·月
第一档电价的基础上每度电加收元
三档
超出度/户·月
第一档电价的基础上每度电加收元