
初中北师大版1 探索勾股定理教案
展开一、知识与技能
让学生通过观察、计算、猜想、验证直角三角形两条直角边的平方和等于斜边的平方的结论.
二、过程与方法
1.在学生充分观察、归纳、猜想、探索直角三角形两条直角边的平方和等于斜边的平方的过程中,发展合情推理能力,体会数形结合的思想.
2.在探索上述结论的过程中,发展学生归纳、概括和有条件地表达活动的过程和结论.
三、情感态度与价值观
1.培养学生积极参与、合作交流的意识.
2.在探索勾股定理的过程中,体验获得结论的快乐,锻炼克服困难的勇气.
学情分析
八年级学生已初步具有几何图形的观察,几何证明的理论思维能力。他们希望老师创设便于他们进行观察的几何环境,给他们发表自己见解和表现自己才华的机会,希望老师满足他们的创造愿望,让他们实际操作,使他们获得施展自己创造才能的机会。但对于勾股定理的得出,首先需要学生通过动手操作,在观察的基础上,大胆猜想数学结论,而这需要学生具备一定的分析、归纳的思维方法和运用数学的思想意识,但学生在这一方面的可预见性和耐挫折能力并不是很成熟,从而形成困难。老师要注意在适当的时机介入指导点拨。
教学重点 探索直角三角形两条直角边的平方和等于斜边的平方的结论,从而发现勾股定理.
教学难点 以直角三角形的边为边的正方形面积的计算.
教具准备 学生准备若干张方格纸;多媒体课件演示.
教学过程
一、创设问题情境,引入新课.
1.学习目标:1)探索直角三角形两条直角边的平方和与斜边的平方的关系。
2)发展合情推理能力,体会数形结合的思想.
2. 有八个直角边长为1的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗?
请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?
由上面的条件可知,这三个正方形的边长分别是1、1, 那么刚才的面积关系可以用一个等量关系式来描述吗?请你写出这个等式.
两条直角边的平方和等于斜边的平方.
这里的等腰直角三角形如果腰长不是1,而是其他数,还会有刚才的结论吗?
进一步思考:是不是所有的直角三角形都是这样的呢?
二、实际操作,合作探索直角三角形的三边关系
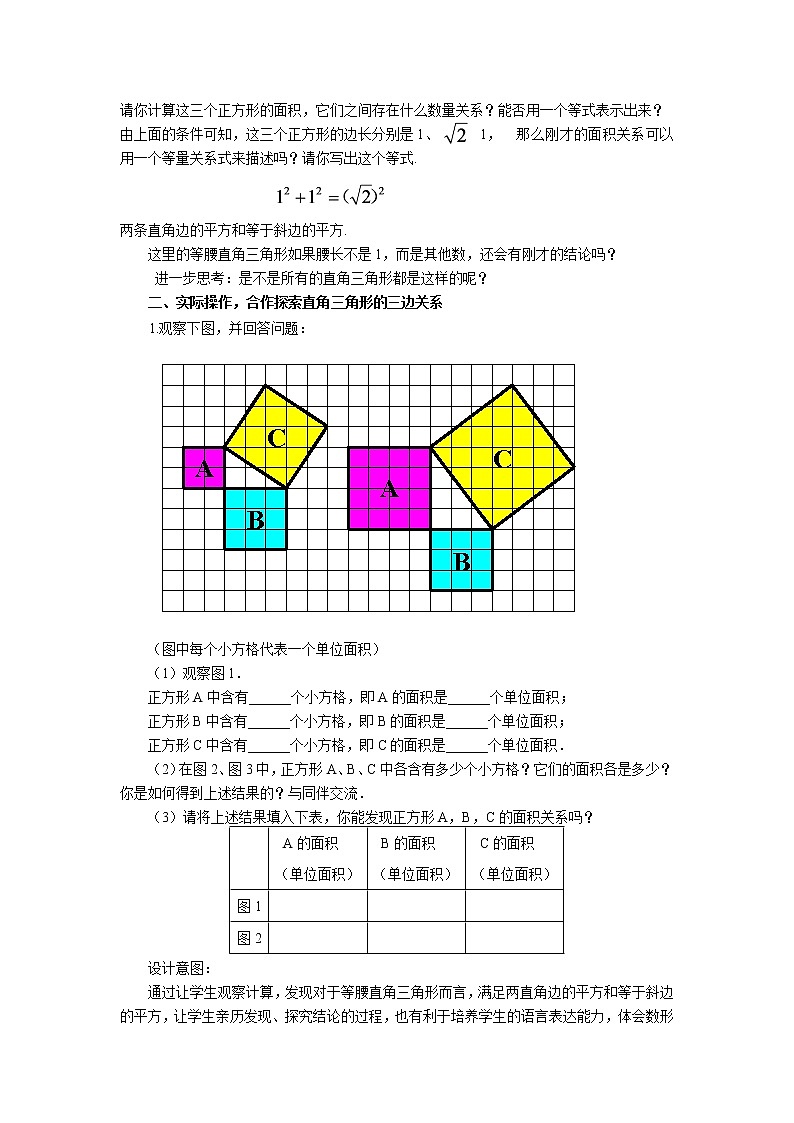
1.观察下图,并回答问题:
(图中每个小方格代表一个单位面积)
(1)观察图1.
正方形A中含有______个小方格,即A的面积是______个单位面积;
正方形B中含有______个小方格,即B的面积是______个单位面积;
正方形C中含有______个小方格,即C的面积是______个单位面积.
(2)在图2、图3中,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流.
(3)请将上述结果填入下表,你能发现正方形A,B,C的面积关系吗?
设计意图:
通过让学生观察计算,发现对于等腰直角三角形而言,满足两直角边的平方和等于斜边的平方,让学生亲历发现、探究结论的过程,也有利于培养学生的语言表达能力,体会数形结合的思想.
师生行为:
要留给学生充分的思考时间,然后让学生交流合作,得出结论.
可让学生在自己准备好的小方格纸上画出,并计算A、B、C三个正方形的面积,并在小组内交流.
设计意图:
进一步让学生体会观察、猜想、归纳这一数学结论发现的过程,也让学生的分析问题和解决问题的能力在无形中得到提高,让学生体会到结论更具一般性.
勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方.
2. 证明定理:请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.(分组合作)
3.结合几何画板演示证明勾股定理。
四、课堂检测: 1. 已知Rt△ABC中,∠C=90°,若a=3,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
(变式:把“∠B=90°”这个条件去掉,分类讨论计算结果。)
3. 一木杆在离地面3 m处折断,木杆顶端落在离木杆底端4 m处. 木杆折断之前有多高?
五、课时小结:
本课我们学习了哪些知识?用了哪些方法?你有哪些体会?
(1.掌握勾股定理的证明及其应用;数形结合思想,从特殊到一般的数学思想。
2.会构造直角三角形,利用勾股定理理解简单应用题。)
六、布置作业:
1. 请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
七、板书设计: 17.1勾股定理(1)
勾股定理的证明
勾股定理的公式变形 例题
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)
图1
图2
数学八年级上册第一章 勾股定理1 探索勾股定理教学设计及反思: 这是一份数学八年级上册第一章 勾股定理1 探索勾股定理教学设计及反思,共7页。教案主要包含了知识与技能,过程与方法,情感、态度与价值观等内容,欢迎下载使用。
初中数学北师大版八年级上册第一章 勾股定理1 探索勾股定理教案设计: 这是一份初中数学北师大版八年级上册第一章 勾股定理1 探索勾股定理教案设计,共4页。
北师大版八年级上册1 探索勾股定理教案: 这是一份北师大版八年级上册1 探索勾股定理教案,共6页。教案主要包含了让学生主动想学,教会学生思维,培养学生多种能力,注重了数学应用意识的培养等内容,欢迎下载使用。













