2022年新高考一轮复习考点精选练习42《圆锥曲线的综合问题》（含详解）

这是一份2022年新高考一轮复习考点精选练习42《圆锥曲线的综合问题》（含详解），共7页。

若双曲线E：eq \f(x2,a2)－y2=1(a＞0)的离心率等于eq \r(2)，直线y=kx－1与双曲线E的右支交于A，B两点.
(1)求k的取值范围；
(2)若|AB|=6eq \r(3)，求k的值.
如图，椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)=1(a>b>0)的右顶点为A(2,0)，左、右焦点分别为F1，F2，过点A且斜率为eq \f(1,2)的直线与y轴交于点P，与椭圆交于另一个点B，且点B在x轴上的射影恰好为点F1.
(1)求椭圆C的标准方程；
(2)过点P且斜率大于eq \f(1,2)的直线与椭圆交于M，N两点(|PM|>|PN|)，若S△PAM∶S△PBN=λ，
求实数λ的取值范围.
已知椭圆C：eq \f(x2,a2)＋eq \f(y2,b2)=1(a>b>0)的左右焦点分别为F1，F2，若椭圆上一点P满足|PF1|＋|PF2|=4，且椭圆C过点(-1,-1.5)，过点R(4,0)的直线l与椭圆C交于E，F两点.
(1)求椭圆C的方程；
(2)过点E作x轴的垂线，交椭圆C于点N，求证：直线FN过定点.
已知抛物线C：y2=2px(p＞0)的焦点为F，准线为l，过焦点F的直线交C于A(x1，y1)，
B(x2，y2)两点，y1y2=－4.
(1)求抛物线C的方程；
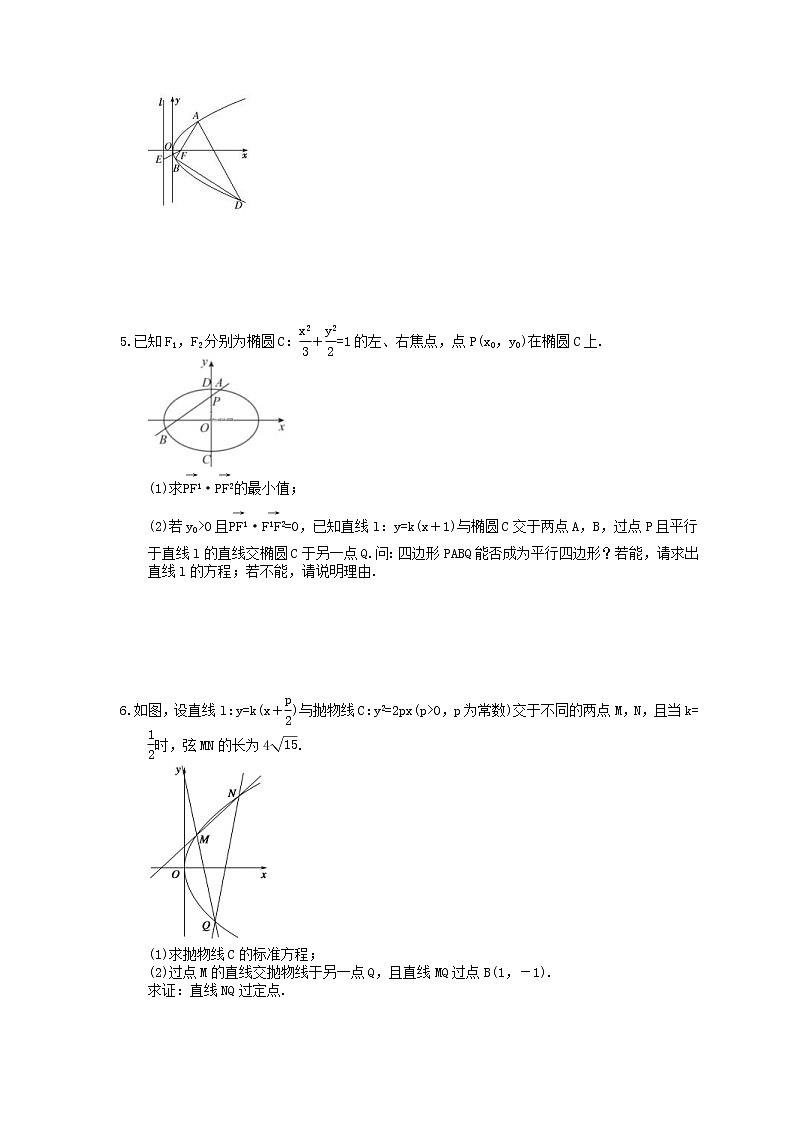
(2)如图，点B在准线l上的正投影为E，D是C上一点，且AD⊥EF，求△ABD面积的最小值及此时直线AD的方程.
已知F1，F2分别为椭圆C：eq \f(x2,3)＋eq \f(y2,2)=1的左、右焦点，点P(x0，y0)在椭圆C上.
(1)求eq \(PF1,\s\up15(→))·eq \(PF2,\s\up15(→))的最小值；
(2)若y0>0且eq \(PF1,\s\up15(→))·eq \(F1F2,\s\up15(→))=0，已知直线l：y=k(x＋1)与椭圆C交于两点A，B，过点P且平行于直线l的直线交椭圆C于另一点Q.问：四边形PABQ能否成为平行四边形？若能，请求出直线l的方程；若不能，请说明理由.
如图，设直线l：y=k(x＋eq \f(p,2))与抛物线C：y2=2px(p>0，p为常数)交于不同的两点M，N，且当k=eq \f(1,2)时，弦MN的长为4eq \r(15).
(1)求抛物线C的标准方程；
(2)过点M的直线交抛物线于另一点Q，且直线MQ过点B(1，－1).
求证：直线NQ过定点.
\s 0 答案解析
解：(1)由eq \b\lc\{(\a\vs4\al\c1(\f(c,a)＝\r(2)，,a2＝c2－1，))得eq \b\lc\{(\a\vs4\al\c1(a2＝1，,c2＝2，))故双曲线E的方程为x2－y2=1.
设A(x1，y1)，B(x2，y2)，由eq \b\lc\{(\a\vs4\al\c1(y＝kx－1，,x2－y2＝1，))得(1－k2)x2＋2kx－2=0.①
∵直线与双曲线的右支交于A，B两点，
∴eq \b\lc\{(\a\vs4\al\c1(1－k2≠0，,Δ＝（2k）2－4（1－k2）·（－2）＞0，,\f(－2,1－k2)＞0，,\f(－2k,1－k2)＞0，))
∴1＜k＜eq \r(2).
(2)由①得x1＋x2=eq \f(2k,k2－1)，x1x2=eq \f(2,k2－1)，
∴|AB|=eq \r(1＋k2)·eq \r(（x1＋x2）2－4x1x2)=2eq \r(\f(（1＋k2）（2－k2）,（k2－1）2))=6eq \r(3)，
整理得28k4－55k2＋25=0，∴k2=eq \f(5,7)或k2=eq \f(5,4).
又1＜k＜eq \r(2)，∴k=eq \f(\r(5),2).
解：(1)因为BF1⊥x轴，得到点B（-c，－eq \f(b2,a2)），
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝2，,\f(b2,aa＋c)＝\f(1,2)，,a2＝b2＋c2，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝2，,b＝\r(3)，,c＝1，))
所以椭圆C的标准方程是eq \f(x2,4)＋eq \f(y2,3)=1.
(2)因为eq \f(S△PAM,S△PBN)=eq \f(\f(1,2)|PA||PM|·sin∠APM,\f(1,2)|PB||PN|·sin∠BPN)=eq \f(2·|PM|,1·|PN|)=λ，所以eq \f(|PM|,|PN|)=eq \f(λ,2)(λ>2)，
所以eq \(PM,\s\up6(→))=－eq \f(λ,2)eq \(PN,\s\up6(→)).由(1)可知P(0，－1)，
设MN方程为y=kx－1，M(x1，y1)，N(x2，y2)，
联立eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx－1，,\f(x2,4)＋\f(y2,3)＝1，))得(4k2＋3)x2－8kx－8=0，Δ>0恒成立，
即得eq \b\lc\{\rc\ (\a\vs4\al\c1(x1＋x2＝\f(8k,4k2＋3)，,x1·x2＝\f(－8,4k2＋3)，))(*)
又eq \(PM,\s\up6(→))=(x1，y1＋1)，eq \(PN,\s\up6(→))=(x2，y2＋1)，有x1=－eq \f(λ,2)x2，
将x1=－eq \f(λ,2)x2代入(*)可得，eq \f(2－λ2,λ)=eq \f(16k2,4k2＋3).
因为k>eq \f(1,2)，所以eq \f(16k2,4k2＋3)=eq \f(16,\f(3,k2)＋4)∈(1,4)，
则12，即得4<λ<4＋2eq \r(3).
综上所述，实数λ的取值范围为(4,4＋2eq \r(3)).
解：(1)依题意，|PF1|＋|PF2|=2a=4，故a=2.
将(-1,-1.5)代入eq \f(x2,4)＋eq \f(y2,b2)=1中，解得b2=3，
故椭圆C的方程是eq \f(x2,4)＋eq \f(y2,3)=1.
(2)证明：由题意知直线l的斜率必存在，设l的方程为y=k(x－4).
点E(x1，y1)，F(x2，y2)，N(x1，－y1)，
联立eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx－4，,3x2＋4y2＝12))得3x2＋4k2(x－4)2=12，
即(3＋4k2)x2－32k2x＋64k2－12=0，
则Δ>0，x1＋x2=eq \f(32k2,3＋4k2)，x1x2=eq \f(64k2－12,3＋4k2).
由题可得直线FN方程为y＋y1=eq \f(y2＋y1,x2－x1)(x－x1).
又∵y1=k(x1－4)，y2=k(x2－4)，
∴直线FN方程为y＋k(x1－4)=eq \f(kx2－4＋kx1－4,x2－x1)(x－x1)，
令y=0，整理得
x=eq \f(x1x2－4x2－x\\al(2,1)＋4x1,x1＋x2－8)＋x1=eq \f(2x1x2－4x1＋x2,x1＋x2－8)=eq \f(2×\f(64k2－12,3＋4k2)－4×\f(32k2,3＋4k2),\f(32k2,3＋4k2)－8)=eq \f(\f(－24,3＋4k2),\f(－24,3＋4k2))=1，
即直线FN过点(1,0).
解：(1)依题意知Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))，
当直线AB的斜率不存在时，y1y2=－p2=－4，解得p=2.
当直线AB的斜率存在时，设lAB：y=keq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(p,2)))(k≠0)，
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝k\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(p,2)))，,y2＝2px，))消去x并整理，得y2－eq \f(2p,k)y－p2=0，
则y1y2=－p2，由y1y2=－4得p2=4，解得p=2.
综上所述，抛物线C的方程为y2=4x.
(2)设D(x0，y0)，Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(t2,4)，t))，
则E(－1，t)，又由y1y2=－4，可得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,t2)，－\f(4,t))).
因为kEF=－eq \f(t,2)，AD⊥EF，所以kAD=eq \f(2,t)，
则直线AD：y＋eq \f(4,t)=eq \f(2,t)eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(4,t2)))，化简得2x－ty－4－eq \f(8,t2)=0.
由eq \b\lc\{\rc\ (\a\vs4\al\c1(2x－ty－4－\f(8,t2)＝0，,y2＝4x，))消去x并整理，得y2－2ty－8－eq \f(16,t2)=0，
Δ=(－2t)2－4eq \b\lc\(\rc\)(\a\vs4\al\c1(－8－\f(16,t2)))=4t2＋eq \f(64,t2)＋32＞0恒成立，
所以y1＋y0=2t，y1y0=－8－eq \f(16,t2).
于是|AD|= eq \r(1＋\f(t2,4))|y1－y0|= eq \r(1＋\f(t2,4)) eq \r(y1＋y02－4y1y0)=eq \r(4＋t2) eq \r(t2＋\f(16,t2)＋8)，
设点B到直线AD的距离为d，则d=eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(\f(t2,2)－t2－4－\f(8,t2))),\r(4＋t2))=eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(t2＋\f(16,t2)＋8)),2\r(4＋t2)).
所以S△ABD=eq \f(1,2)|AD|·d=eq \f(1,4) eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(t2＋\f(16,t2)＋8))3)≥16，
当且仅当t4=16，即t=±2时取等号，即△ABD的最小值为16.
当t=2时，直线AD：x－y－3=0；当t=－2时，直线AD：x＋y－3=0.
解：(1)由题意可知，F1(－1,0)，F2(1,0)，
∴eq \(PF1,\s\up15(→))=(－1－x0，－y0)，eq \(PF2,\s\up15(→))=(1－x0，－y0)
∴eq \(PF1,\s\up15(→))·eq \(PF2,\s\up15(→))=xeq \\al(2,0)＋yeq \\al(2,0)－1
∵点P(x0，y0)是椭圆C上，∴eq \f(x\\al(2,0),3)＋eq \f(y\\al(2,0),2)=1，即yeq \\al(2,0)=2－eq \f(2x\\al(2,0),3)
∴eq \(PF1,\s\up15(→))·eq \(PF2,\s\up15(→))=xeq \\al(2,0)＋2－eq \f(2,3)xeq \\al(2,0)－1=eq \f(1,3)xeq \\al(2,0)＋1，且－eq \r(3)≤x0≤eq \r(3)
∴eq \(PF1,\s\up15(→))·eq \(PF2,\s\up15(→))最小值1.
(2)∵eq \(PF1,\s\up15(→))·eq \(F1F2,\s\up15(→))=0，∴x0=－1，
∵y0>0，∴Peq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(2\r(3),3)))设A(x1·y1)，B(x2，y2).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx＋1，,\f(x2,3)＋\f(y2,2)＝1))得，(2＋3k2)x2＋6k2x＋3k2－6=0，
∴x1＋x2=－eq \f(6k2,2＋3k2)，x1x2=eq \f(3k2－6,2＋3k2)，
∴|x1－x2|=eq \r(x1＋x22－4x1x2)=eq \f(4\r(3)·\r(1＋k2),2＋3k2)，
∴|AB|=eq \r(1＋k2)·|x1－x2|=eq \f(4\r(3)·1＋k2,2＋3k2)
∵Peq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(2\r(3),3)))，PQ∥AB，∴直线PQ的方程为y－eq \f(2\r(3),3)=k(x＋1).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y－\f(2\r(3),3)＝kx＋1,\f(x2,3)＋\f(y2,2)＝1))得，(2＋3k2)x2＋6keq \b\lc\(\rc\)(\a\vs4\al\c1(k＋\f(2\r(3),3)))x＋3eq \b\lc\(\rc\)(\a\vs4\al\c1(k＋\f(2\r(3),3)))2－6=0.
∵xP=－1，∴xQ=eq \f(2－3k2－4\r(3)k,2＋3k2)，
∴|PQ|=eq \r(1＋k2)·|xP－xQ|=eq \r(1＋k2)·eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(4－4\r(3)k)),2＋3k2)，
若四边形PABQ能成为平行四边形，则|AB|=|PQ|，
∴4eq \r(3)·eq \r(1＋k2)=|4－4eq \r(3)k|，解得k=－eq \f(\r(3),3).
∴符合条件的直线l的方程为y=－eq \f(\r(3),2)(x＋1)，
即x＋eq \r(3)y＋1=0.
解：(1)设M(x1，y1)，N(x2，y2)，当k=eq \f(1,2)时，直线l：y=eq \f(1,2)(x＋eq \f(p,2))，即x=2y－eq \f(p,2)，
联立方程，得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝2y－\f(p,2)，,y2＝2px，))即y2－4py＋p2=0.
∴y1＋y2=4p，y1y2=p2，
于是得|MN|=eq \r(1＋4)|y1－y2|=eq \r(5)×eq \r(y1＋y22－4y1y2)=2eq \r(15)|p|=4eq \r(15)，
因为p>0，所以p=2，即抛物线C的标准方程为y2=4x.
(2)证明：设点M(4t2,4t)，N(4teq \\al(2,1)，4t1)，Q(4teq \\al(2,2)，4t2)，
易得直线MN，MQ，NQ的斜率均存在，则直线MN的斜率是kMN=eq \f(4t－4t1,4t2－4t\\al(2,1))=eq \f(1,t＋t1)，
从而直线MN的方程是y=eq \f(1,t＋t1)(x－4t2)＋4t，即x－(t＋t1)y＋4tt1=0.
同理可知MQ的方程是x－(t＋t2)y＋4tt2=0，NQ的方程是x－(t1＋t2)y＋4t1t2=0.
又易知点(－1,0)在直线MN上，
从而有4tt1=1，即t=eq \f(1,4t1)，点B(1，－1)在直线MQ上，
从而有1－(t＋t2)×(－1)＋4tt2=0，
即1－(eq \f(1,4t1)＋t2)×(－1)＋4×eq \f(1,4t1)×t2=0，
化简得4t1t2=－4(t1＋t2)－1.
代入NQ的方程得x－(t1＋t2)y－4(t1＋t2)－1=0.
所以直线NQ过定点(1，－4).