数学1.3 三角函数的诱导公式课文配套ppt课件
展开1.3 三角函数的诱导公式
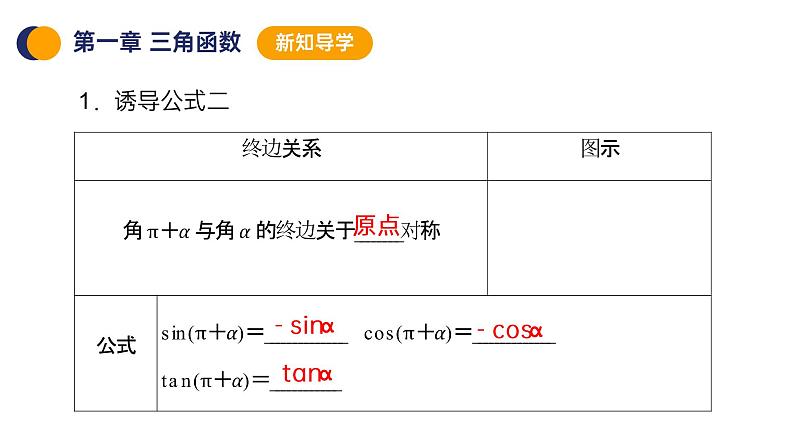
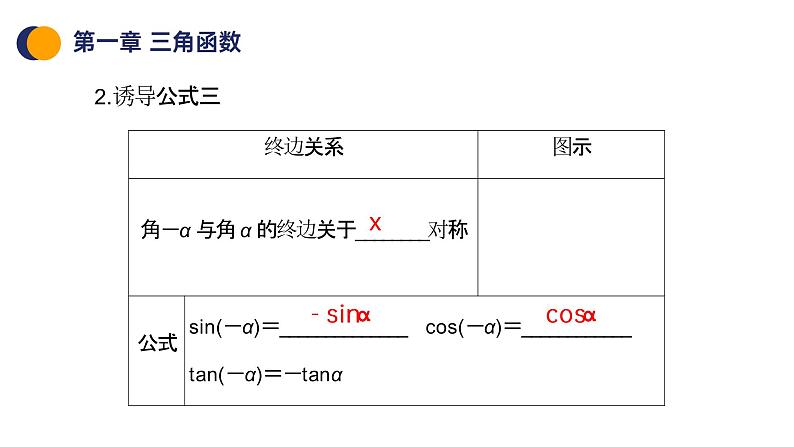
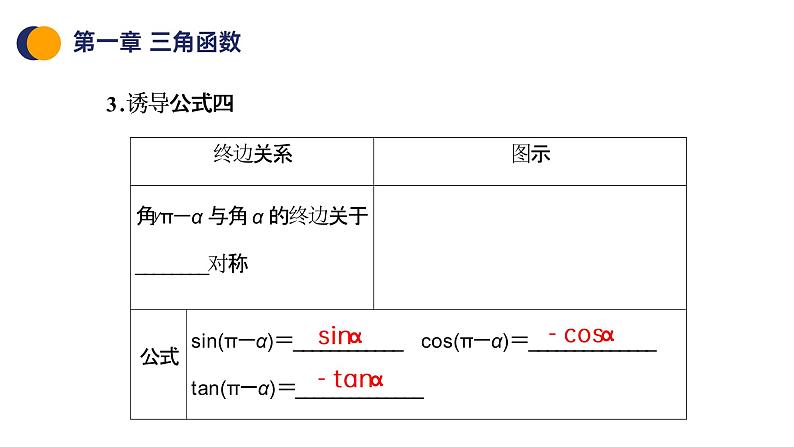
第1课时 诱导公式二、三、四
对称美是日常生活中最常见的,在三角函数中-α、π±α、2π-α等角的终边与角α的终边关于坐标轴或原点对称,那么它们的三角函数值之间是否也存在对称美呢?
特别提醒:1.公式一~四中的角α是任意角.2.公式一、二、三、四都叫做诱导公式,它们可概括如下:(1)记忆方法:2kπ+α(k∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号,可以简单地说成“函数名不变,符号看象限”.(2)解释:“函数名不变”是指等式两边的三角函数同名;“符号”是指等号右边是正号还是负号;“看象限”是指假设α是锐角,要看原三角函数值是取正值还是负值,如sin(π+α),若把α看成锐角,则π+α是第三象限角,故sin(π+α)=-sinα.
3.诱导公式的作用(1)公式一的作用在于把绝对值大于2π的任一角的三角函数问题转化为绝对值小于2π的角的三角函数问题.(2)公式三的作用在于把负角的三角函数转化成正角的三角函数.(3)公式二、公式四的作用在于把钝角或大于180°的角的三角函数转化为0°~90°之间的角的三角函数.
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.(1)三角函数诱导公式中的角α应为锐角.( )(2)存在角α,使sin(π+α)=sinα,cs(π-α)=csα.( )(3)当α是第三象限角时,tan(-α)=tanα.( )(4)tan(α-π)=tanα.( )(5)若α,β满足α+β=π,则sinα=sinβ且tanα=tanβ.( )
命题方向1 ⇨利用诱导公式解决给角求值问题
『规律总结』 利用诱导公式求任意角三角函数的步骤:(1)“负化正”——用公式一或三来转化.(2)“大化小”——用公式一将角化为0°到360°间的角.(3)“小化锐”——用公式二或四将大于90°的角转化为锐角.(4)“锐求值”——得到锐角的三角函数后求值.
命题方向2 ⇨三角函数式的化简问题
『规律总结』 利用诱导公式一~四化简应注意的问题:(1)利用诱导公式主要是进行角的转化,从而达到统一角的目的.(2)化简时函数名不发生改变,但一定要注意函数的符号有没有改变.(3)同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切.
在利用诱导公式进行运算求解时,无论α是否真的是锐角,我们都要把α看作是锐角,这就是作题时需要具备的“整体”思想 .
『规律总结』 解决条件求值问题策略:解决条件求值问题,要仔细观察条件与所求式之间的角、函数名及有关运算之间的差异及联系,要么将已知式进行变形向所求式转化,要么将所求式进行变形向已知式转化.总之,设法消除已知式与所求式之间的种种差异是解决问题的关键,使用诱导公式时要用到“整体”思想.
设θ是钝角,则cs(2π-θ)=_________.[错解] 因为θ是钝角,所以2π-θ是第三象限,而第三象限角的余弦值是负值,所以cs(2π-θ)=-csθ,故填-csθ.[错因分析] 上面的解法没有理解使用公式时视角θ为锐角的意义,一般地,视θ为锐角,则2π+θ,π-θ,π+θ,2π-θ分别是第一、第二、第三、第四象限角.[正解] csθ 视θ为锐角,则2π-θ为第四象限角,所以cs(2π-θ)=csθ,故填csθ.
对诱导公式理解不透致错
高中数学人教A版 (2019)必修 第一册5.3 诱导公式背景图ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册5.3 诱导公式背景图ppt课件,共19页。PPT课件主要包含了是用什么方法研究的,复习引入,新课引入,学习新知,终边互为反向延长线,从而得到诱导公式二,终边关于x轴对称,终边关于y轴对称,从而得到公式三,同理可得公式四等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式教学演示课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式教学演示课件ppt,共20页。PPT课件主要包含了学习目标,公式一,其特征是,公式三,探究2,公式二,探究3,公式四,例3化简,答案-2等内容,欢迎下载使用。
2020-2021学年1.3 三角函数的诱导公式说课课件ppt: 这是一份2020-2021学年1.3 三角函数的诱导公式说课课件ppt,共22页。PPT课件主要包含了问题提出,°+α,Q-x-y,公式二,Px-y,公式三,公式四,Pxy,P-xy,理论迁移等内容,欢迎下载使用。