2021学年2.4 圆周角教案设计

这是一份2021学年2.4 圆周角教案设计，共5页。
课题：2.4 圆周角（1）
教学目标
1．了解圆周角的概念；
2．让学生经历圆周角与圆心角关系的探索过程，培养学生的动手操作、自主探索和合作交流的能力；
3．能用圆周角与圆心角的关系进行简单的说理，培养学生合情推理的意识，掌握说理的基本方法，从而提高数学素养．
教学重点
探索圆周角与圆心角的关系．
教学难点
通过分类讨论，推理、验证“圆周角与圆心角的关系”．
教学过程（教师）
学生活动
设计思路
情境引入
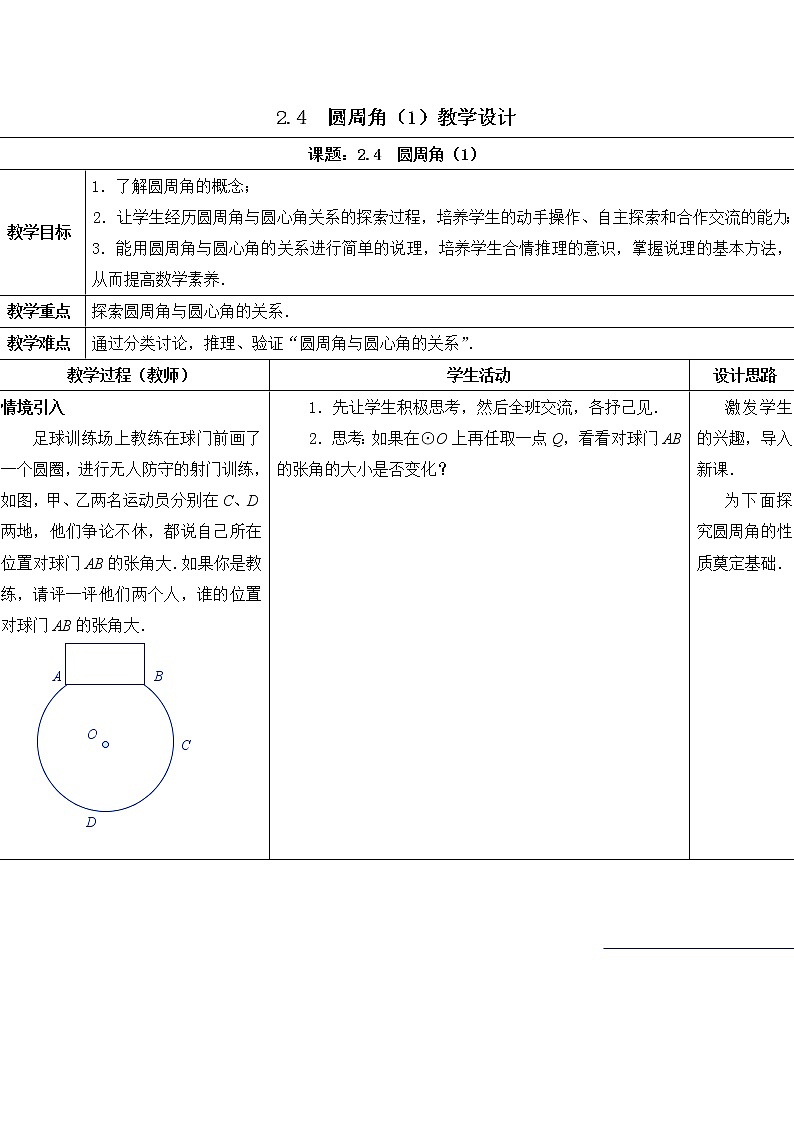
足球训练场上教练在球门前画了一个圆圈，进行无人防守的射门训练，如图，甲、乙两名运动员分别在C、D两地，他们争论不休，都说自己所在位置对球门AB的张角大．如果你是教练，请评一评他们两个人，谁的位置对球门AB的张角大．
A
B
O
C
D
1．先让学生积极思考，然后全班交流，各抒己见．
2．思考：如果在⊙O上再任取一点Q，看看对球门AB的张角的大小是否变化？
激发学生的兴趣，导入新课．
为下面探究圆周角的性质奠定基础．
实践探索一：圆周角的概念
教师：在上面的角有什么特征？如果请你命名，你叫它什么？
顶点在圆上，两边都和圆相交的角叫做圆周角．
1．让学生自由的说，并说出命名的理由．
2．口答：判断下列各图中的角是否是圆周角？
并说明理由．
让学生加深对圆周角概念的理解．
巩固给出圆周角的概念．
实践探索二：圆周角的性质
1．操作猜想：
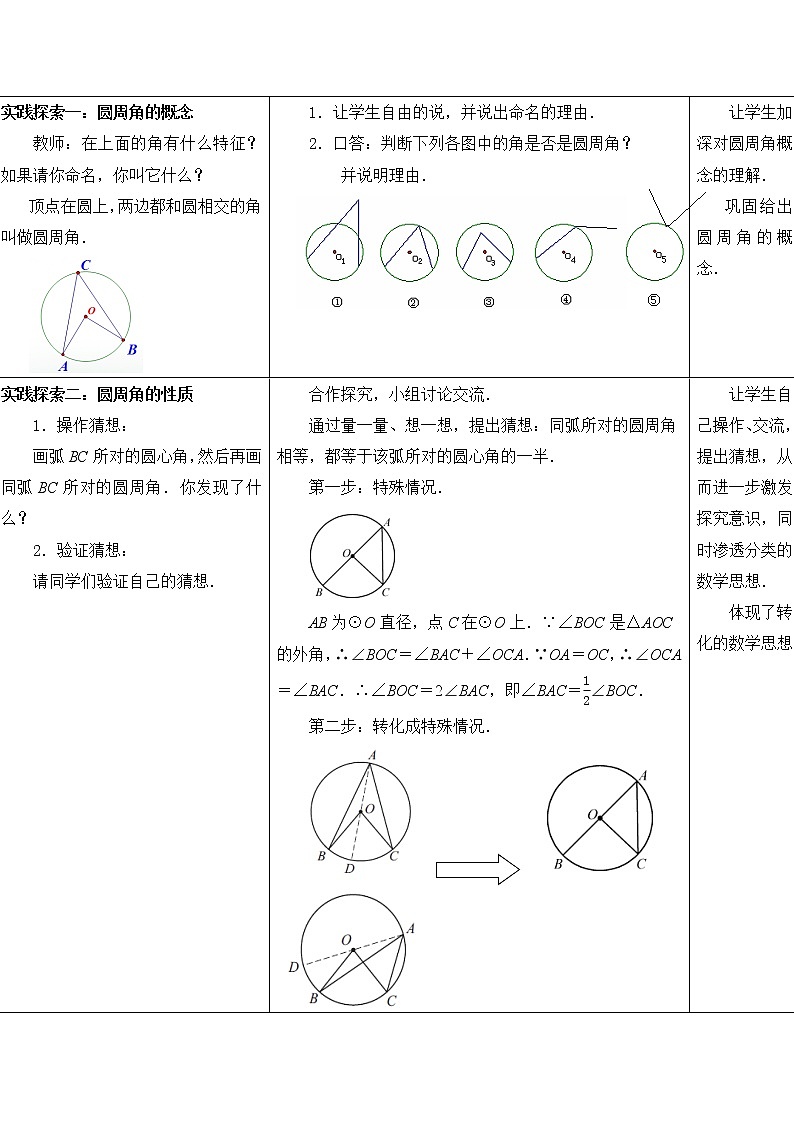
画弧BC所对的圆心角，然后再画同弧BC所对的圆周角．你发现了什么？
2．验证猜想：
请同学们验证自己的猜想．
合作探究，小组讨论交流．
通过量一量、想一想，提出猜想：同弧所对的圆周角相等，都等于该弧所对的圆心角的一半．
第一步：特殊情况．
AB为⊙O直径，点C在⊙O上．∵∠BOC是△AOC的外角，∴∠BOC＝∠BAC＋∠OCA．∵OA＝OC，∴∠OCA＝∠BAC．∴∠BOC＝2∠BAC，即∠BAC＝ eq \f(1,2)∠BOC．
第二步：转化成特殊情况．

定理：在同圆或等圆中，
同弧或等弧所对的圆周角相等，
都等于该弧所对的圆心角的一半．
让学生自己操作、交流，提出猜想，从而进一步激发探究意识，同时渗透分类的数学思想．
体现了转化的数学思想．
例题讲解
例1 如图，⊙O的弦AB、DC的延长线相交于点E，∠AOD＝150°， eq \(\s\up 6(⌒),BC)为70°．求∠ABD、∠AED的度数．
1．先让学生独立思考，然后让学生板演，最后学生点评．
（引导学生从已知条件入手，逐一进行分析，得到哪些结论？）
知识点的综合运用，进行适当的变式，进一步内化所学的知识．
例2 如图，P是△ABC的外接圆上的一点，∠APC＝∠CPB＝60°．
求证：△ABC是等边三角形．
2．先让学生独立思考，然后请学生讲评．
练一练
如图，点A、B、C、D在⊙O上，∠BAC＝35° ．
（1）∠BDC＝ °，
理由是 ；
（2）∠BOC＝ °，
理由是 ．
独立思考，集体反馈．
巩固所学知识．
拓展提升
如图，点A、B、C在⊙O上，点D在圆外，CD、BD分别交⊙O于点E、F，比较∠BAC与∠BDC的大小，并说明理由．

变式：移动点D到圆内，其它条件不变，此时∠BAC与∠BDC的大小又如何？并说明理由．
解：连接CF，
∵ ∠BFC是△DFC的一个外角，
∴ ∠BFC ＞ ∠BDC ．
∵ ∠BAC ＝∠BFC（同弧所对的圆周角相等）．
∴ ∠BAC ＞ ∠BDC．

总结
这节课你有哪些收获和困惑？开始的问题情境，你解决了吗？
各抒己见．
培养学生归纳、口头表达能力．
课后作业
课本P55-56第1、2、3．
独立完成．
进一步复习巩固所学知识．